城市干道交通信號協調控制優化設計

周 君

（淮陰工學院交通工程系 淮安 223003）

城市主干道是城市交通的主要承擔者，主干道上的交叉口成為干道交通通行能力的瓶頸，將干道上若干個交叉口的交通信號進行聯動控制，可以大大提高干道交通通行能力.城市干道協調控制的傳統設計方法通常有2種：圖解法，數解法.圖解法是在時間－距離圖上通過幾何的方法來得到近似解；而數解法則是通過尋找使得系統中各實際信號距離理想信號的最大挪移量最小的相位差來獲得最優控制方案［1］.這2種方法原理簡單，使用較廣.自20世紀末以來有很多學者提出改進的基于解析模型的交叉口干道協調控制及其求解方法，其中最著名的是J.D.C.Little［2］提出的Maxband協調控制模型，對給定周期時長、綠信比、信號間距和連續行車速優化相位差以獲得最大帶寬，并提出了混合整數線性規劃求解方法；Gartner［3］等人在基于 Maxband的基礎上研究了Multiband模型，克服了Maxband帶寬不變的不足，其帶寬與交通需求變化相對應.

1 交叉口簡介以及信號相位的選擇

信號協調控制的交叉口位于淮海南路水門橋到新民西路之間的4個交叉口，見圖1.

圖1中與淮海南路相交的都是支路或次干路，因為與淮海南路交叉的道路上交通流量較小所以都采用三相位的信號控制方式，其中第一相位表示淮海南路直行放行相位，第二相位為淮海南路左轉和右轉放行相位，第三相位為與淮海南路相交叉道路直行、左轉、右轉放行相位.

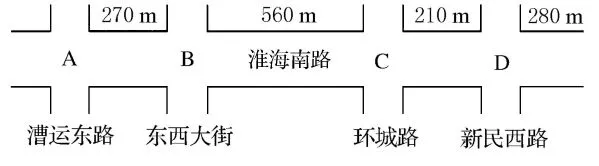
圖1 淮海南路交叉口簡介圖

2 信號協調控制交叉口信號配時

在信號協調控制中，首先要進行配時方案的計算，計算備用配時方案，步驟如下［4］.

1）根據每一交叉口的平面布局及計算交通量，按單點定時控制的配時方法，確定每一交叉口所需的周期時長.

2）以所需的周期時長最大的交叉口為關鍵交叉口，以此周期時長為線控系統的備選系統周期時長.

3）以各交叉口所需的周期時長并根據主次道路的流量比，計算各交叉口各相位的綠信比及顯示綠燈時間.

上步算得的關鍵交叉口上主干道相位顯示綠燈時間，就是各交叉口上對干道方向所必須保持的最小綠燈長度.顯示綠燈時間和有效綠燈時間.

2.1 各交叉口單點信號配時

采用Webster法進行單點信號配時，其各交叉口的單點配時見表1.

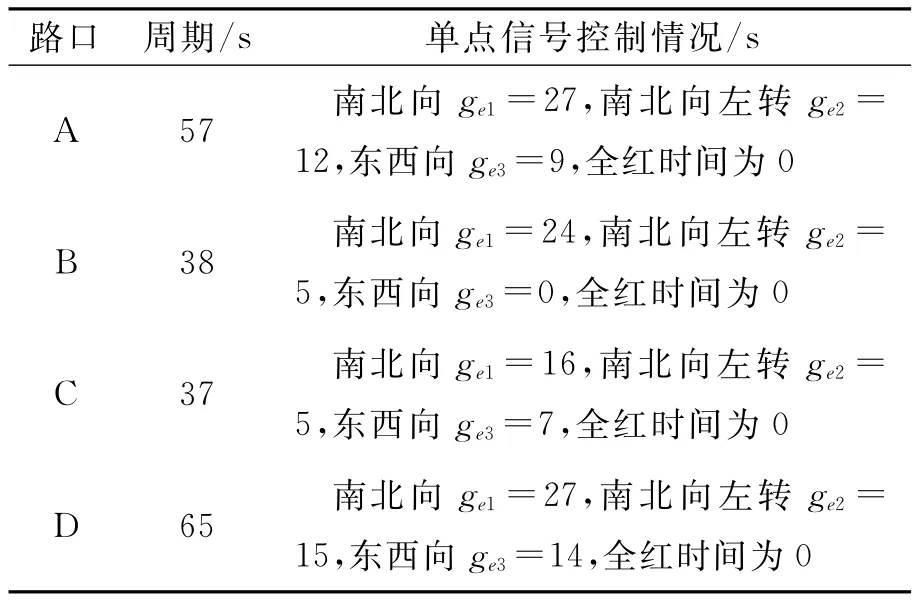
表1 各個交叉口的信號配時方案

表1中因為B路口是淮海南路與東大街與西大街的交叉口，東西方向雖然車流量很小，幾乎可以忽略不計，但是人流量卻非常大，因此，在協調控制時根據以往經驗，東西方向必須保持每周期15s以上的綠燈時間以利于行人的通行.

2.2 交通信號協調控制配時方案［5－6］

將表1中最大的信號周期65s作為系統周期，根據各相位流量比確定各相位的綠燈時間，則各個交叉口的協調信號配時方案如表2和表3.

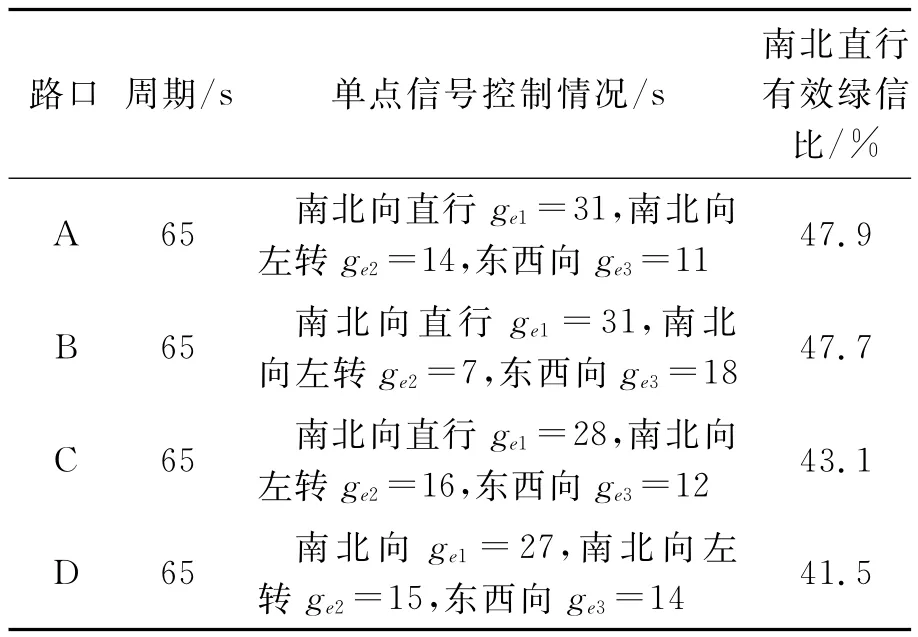
表2 協調控制信號配時方案

3 數解法求解協調控制信號相位差

淮海南路的4個交叉口設為A，B，C，D，其代表的具體交叉口及各交叉口之間的距離見圖1，將A－D中各交叉口的距離寫在表3第二行，并取距離的有效數字，如A－B距離270m寫成27.已得到系統周期為65s，城市中車輛的速度一般為40km／h，則將系統速度暫定為v＝11m／s（40km／h）.

3.1 數解法計算結果

數解法計算結果見表3.

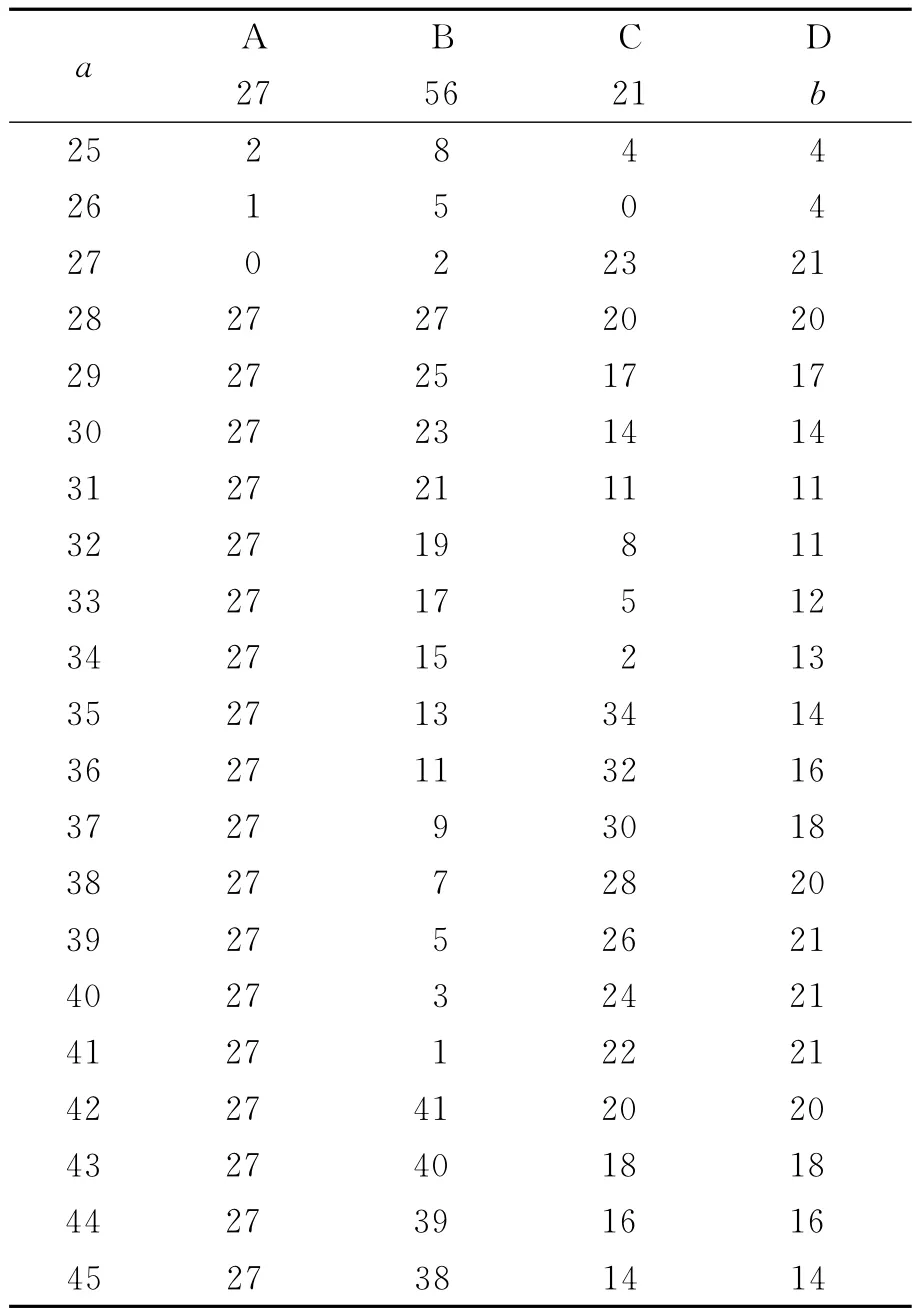
表3 數解法確定各交叉口信號時差

在表3中，以a＝40行為例，將實際信號位置與理想信號位置的挪移量，按順序排列（從小到大）并計算各相鄰挪移量之差，將此值最大者計入b列，a＝27一行的b值為21，計算方法如表4.

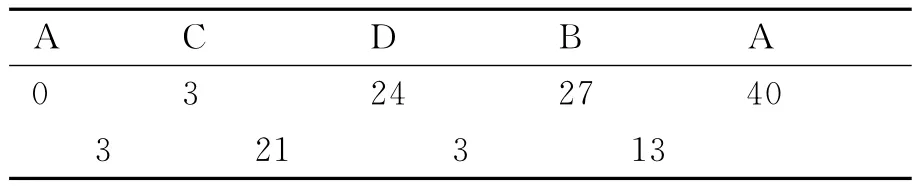
表4 實際信號位置與理想信號位置的挪移量

以此類推，計算a＝25～45各行的b值.

3.2 確定合適的理想信號位置

由表3知，當a＝40，b＝21為最大值，取b為最大值時對應的a的值，即可得A－D各信號到理想信號的挪移量最小，即當vC／2＝400m時，可以得到最好的系統協調效率，如圖2所示，圖上C，D距離理想信號間的挪移差最大為210m.則理想信號同C的挪移量最大為

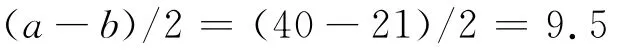
即各實際信號距理想信號的挪移量最大是95m.

理想信號距A為65m，A后移65m即為理想信號的位置，然后依次按每400m間距將各理想信號列在各實際信號間，如圖2所示.

3.3 求信號起始時差［7－11］

從圖2可以看出，合用一個理想信號的左、右相鄰實際信號間，用同步式協調；其他各實際信號間都用交互式協調，因此，每隔一個理想信號的實際信號間又是同步式協調.此時，凡是奇數理想信號相應的實際信號間為同步式協調；而偶數理想信號相應的實際信號間為交互式協調.因此，相應于奇數理想信號的實際信號的時差為100%～0.5λ%（例如，表5中第7行A交叉口相應的是理想信號①，屬于奇數理想信號，那么它的時差為100%～0.5×53.8%＝73.1%）；相應于偶數理想信號的實際信號的時差為50%～0.5λ%（例如，表5中第7行B交叉口相應的是理想信號②，屬于偶數理想信號，那么它的時差為50%～0.5×47.7% ＝26.2%）.與理想信號相位差等于周期與各個綠時差的乘積，其結果如表5中第8行所示.如果保持原定的周期時長，則系統帶速必須調整為：v＝2s／C＝2×400／65＝12.3m／s＝44 km／h.

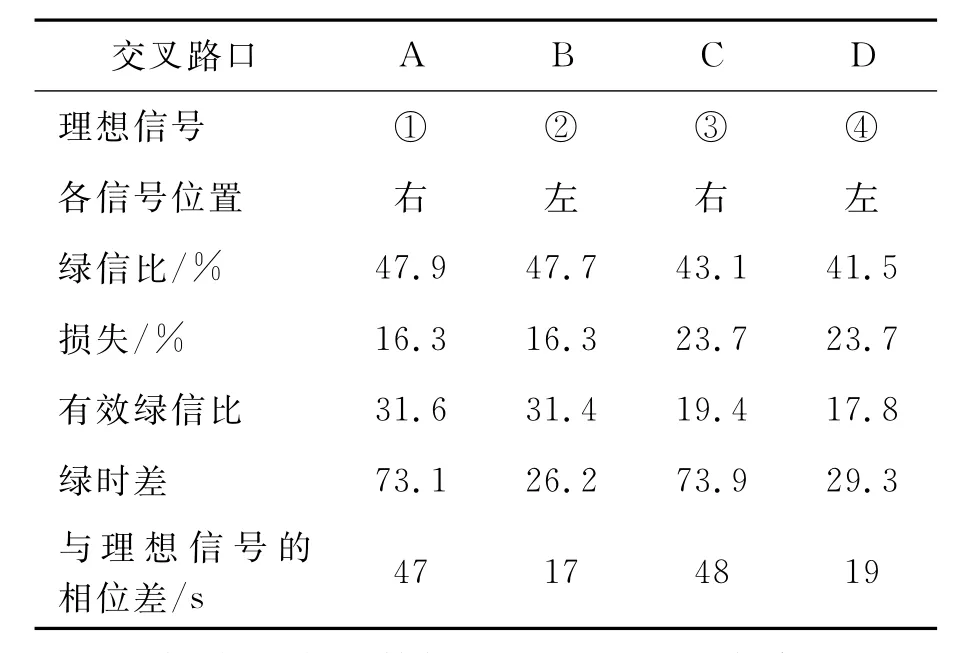
表5 計算綠時差

根據表5中的數據，用CAD繪圖軟件畫出用數解法求出的交通信號相位差時空分布圖，如圖3所示.

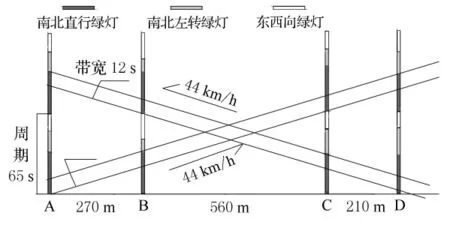
圖3 數解法計算所得時空圖

4 協調控制方案和現行方案的仿真對比

用vissim軟件進行仿真得到本文控制方案與現行控制方案的優劣對比，見表6、圖4.

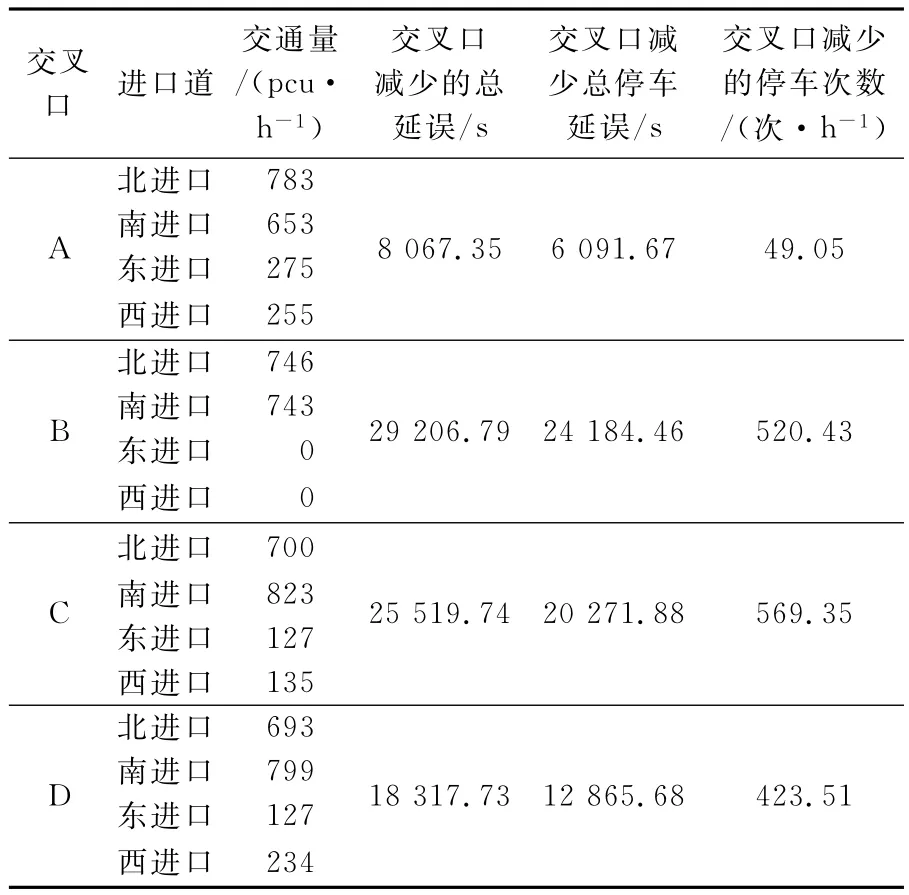
表6 各進口道現行控制方案與本文信號協調控制方仿真情況對比

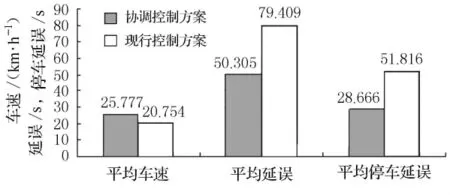
圖4 2個方案路網車輛平均車速、平均延誤和平均停車延誤對比

5 結束語

本文提出的淮安市淮海南路交通信號協調控制不僅使得淮海南路南北直行方向（協調控制方向）的交通運行得到改善，而且各個交叉口以及整個仿真路段的交通運行指標也得到了優化，從而可以得出不管是從宏觀角度還是微觀層面，本文信號協調控制方案比現行控制方案更為優越.從以上表格和圖表中也可以看出，不管是總延誤還是停車延誤或者交叉口停車次數此協調控制方案都比現行控制方案要好，信號協調控制方案極大地改善了交通的運行狀況，尤其是淮海南路的主干道的交通運行秩序得到質的提高.雖然有些支路與淮海南路相交叉的路口的某些進口道方向延誤有所增加，但是由于起交通量較小，所以對大的車輛運行秩序沒有多大影響，從以上直方圖中可以清楚的看出淮海南路實行信號協調控制方案以后，路網總的行程時間和停車延誤以及平均停車延誤都下降很多，所以從宏觀層面本文信號協調控制方案也減少了整個路網的交通擁擠程度.

［1］孫 劍，劉好德，李克平.城市干道交通信號協調控制仿真優化［J］.同濟大學學報：自然科學版，2009，37（11）：1 467－1 471.

［2］Little J D C.The synchronization of traffic signals by mixed－integer linear programming［J］.Operations Re－search，1996，14（1）：568－572.

［3］Gartner N H，Stamatiadis C.Progression optimization featuring arterial－and route－based priority signal networks［J］.Intelligent Transportation System，2004，8（2）：77－81.

［4］栗紅強.城市交通控制信號配時參數優化方法研究［D］.長春：吉林大學交通學院，2004.

［5］宋現敏.交叉口協調控制相位差優化方法研究［D］.長春：吉林大學交通學院，2005.

［6］吳 震，楊曉光.車道寬度、轉彎半徑對左轉飽和流量的影響研究［J］.武漢理工大學學報：交通科學與工程版，2009，33（5）：996－999.

［7］吳 震.基于仿真的干線協調控制分析指標［J］.武漢理工大學學報：交通科學與工程版，2009，33（2）：349－352.

［8］李瑞敏，陸化普，史其信.基于遺傳算法的交通信號多層模糊控制模型研究［J］.武漢理工大學學報：交通科學與工程版，2009，33（3）：407－410.

［9］張 本，商 蕾，高孝洪.基于遺傳算法的交叉口信號配時多目標優化［J］.武漢理工大學學報：交通科學與工程版，2010，34（4）：845－848.

［10］馬永光.城市交通干線信號優化控制方法的研究［D］.天津：天津大學自動化學院，2007.

［11］姜桂艷.道路交通狀態判別技術與應用［M］.北京：人民交通出版社，2004.