關于一類連續型隨機變量的最優區間問題
蘇 強, 程財生
(1.連云港師范高等專科學校,江蘇連云港 222006; 2.防化指揮工程學院數學教研室,北京 102205)
關于一類連續型隨機變量的最優區間問題
蘇 強1, 程財生2
(1.連云港師范高等專科學校,江蘇連云港 222006; 2.防化指揮工程學院數學教研室,北京 102205)
設隨機變量的概率密度函數為R(Rn)上連續函數,給出最優區間(區域)的概念,討論最優區間(區域)的必要條件,并且以四個實例說明最優區間的求解思路.
連續型隨機變量; 最優區間; 最優區域; 概率密度函數
1 引言和結果
在講授概率論這門課程時,我們經常會遇到許多具有相同概率的事件,特別是在同一隨機變量的情況下,實數集R的不同可測子集所對應事件的概率有時是相同的[1]1后者引起了我們的興趣,這促使我們提出了一個關于給定概率的最優可測集的問題,即:設連續型隨機變量ξ,對于任意給定α(0< α<1),考慮所有概率等于α的事件A,問在什么條件下,數集ξ-1(A)測度最小以及如何找出測度最小的ξ-1(A)?簡言之,尋找最小測度的數集,使其對應事件的概率為預先給定值?對于一般的隨機變量來說,這個問題比較復雜1在本文中我們就一類簡單的情形給出上述問題的一個解答1

下面定義連續型隨機變量的最優區間概念:
定義2 設ξ是一連續型隨機變量,對于任意給定的α(0<α<1),如果存在區間[c,d]為使等式成立的長度最小的區間,則稱[c,d]為最優區間1
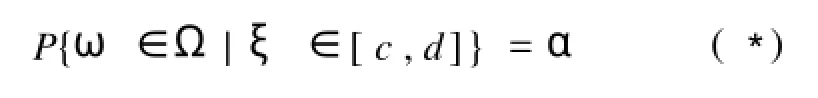
根據定義1,等式(3)可表示為F(d)-F(c)= α 1又知連續型隨機變量的分布函數F(x)具有三個基本性質:①F(x)是實數集R上的連續函數;②F(x)是單調不減的;③=11因此滿足等式(3)的區間存在,并有無窮多個1
關于最優區間的存在性,本文中不作詳細分析1下面給出一類連續型隨機變量關于某個給定概率的最優區間問題的一個必要條件:
定理1 設ξ是一連續型隨機變量,概率密度函數為p(x),x∈(-∞,+∞)1如果p(x)是一連續函數,對于任意給定的α(0<α<1),使得[a,b]為最優區間的必要條件為p(a)=p(b)1
2 定理1的證明與應用舉例
證明:采用反證法1假設p(a)≠p(b)1不妨設p(a) 從而P(x)-P(a)>01這樣,就能縮短區間[x, x+b-a]的長度,因而比[a,b]的長度小,這與[a, b]的長度最小相互矛盾1所以p(a)=p(b)1 定理1給我們提供了一個比較有效的辦法去尋找給定概率的最優區間,下面結合實例來分析. 例1 設隨機變量ξ~N(a,σ2),解釋其最優區間情況. 解:對于正態分布ξ,知其概率密度是關于x=a對稱的,結合上面的定理,我們知道其最優區間是關于x=Eξ=a對稱的,并且最優區間是惟一的1根據標準正態分布表,容易求出給定概率的最優區間. 例2 設隨機變量η~p(x),其中 給定概率后,可知其最優區間關于x=0對稱,觀察概率密度函數p(x)的圖像[2](見圖1),容易推出最優區間也是惟一的1但p(x)的原函數不能用初等函數表出,所以不能具體寫出最優區間. 圖1 注:(1)在上面兩個例子中最優區間是惟一的,而有時最優區間未必惟一; (2)在實際問題中,可能為最優區間的區間個數僅有有限個,只需在他們之間做簡單分析就能找出所求的最優區間1因此,對于滿足定理1條件的隨機變量,我們都能通過必要條件找出給定概率的最優區間,再做一些比較,就能找出最優區間; (3)一些常用的連續型隨機變量其最優區間是比較容易求得,如指數分布ξ~exp(λ)1 下面給出上述理論在高維的推廣. 定義3 設η是一n維連續型隨機變量,對任意給定的α(0<α<1),如果存在一區域D為使得式P{ω∈Ω|η(ω)∈D}=α成立的長度最小的區間,則稱區域D為最優區域. 定理2 設η是多元連續型隨機變量,概率密度函數為p(x1,x2,…,xn),其中(x1,x2,…xn)∈Rn,如果p(x1,x2,…,xn)是Rn上連續函數,對于任意給定的α(0<α<1),使得閉區域D為最優區域的必要條件為p(a)=p(b),其中a,b∈5D. 證明 采用反證法1假設存在兩點a,b∈5D,使得p(a)≠p(b)1可不妨設p(a) 這樣,就能找到更小的區域,從而導致矛盾.因此定理證畢. 注:(4)從幾何的角度看,定理2的最優區域D的邊界5D是概率密度函數p(x1,x2,…,xn)的等高線[3](或等高面); (5)相對于一維連續型隨機變量,多維連續型隨機變量的最優區域更復雜些. 例3 設二維隨機變量(ξ,η)~p(x,y),其中 解:聯合密度函數p(x,y)是平面上連續函數,由定理2可知,最優區域是以原點為中心的圓盤. 對于給定的α(0<α<1),設所對應的圓盤Da的半徑為t,則有 [1]李賢平.概率論[Z].北京:高等教育出版社,1998. [2]王昆揚.簡明數學分析[Z].北京:高等教育出版社, 2001. [3]威廉·費勒.概率論及其應用(第三版)[M],北京:人民郵電出版社,2006. [4]Г.М.菲赫金哥爾茨.微積分學教程(第八版)第一卷[Z].北京:高等教育出版社,2006. Abstract:This paper discusses a necessary condition for the optimal interval(optimal region)of certain continuous random variable with a given probability and illustrates the solving approaches of the optimal interval via four examples. Key words:continuous random variables; optimal interval; optimal region; probability density function On the Optimal Interval of Certain Continuous Random Variables SU Qiang1, CHENG Cai-sheng2 (1.Lianyungang Teachers'College,Lianyungang,Jiangsu 222006; O211.5 A 1671-9743(2011)02-0030-03 2010-01-20 蘇 強(1976-),男,江蘇贛榆人,連云港師范高等專科學校講師,碩士研究生,主要研究高等數學與應用數學; 程財生(1978-),男,江西九江人,北京防化指揮工程學院講師,碩士研究生,主要研究基礎數學1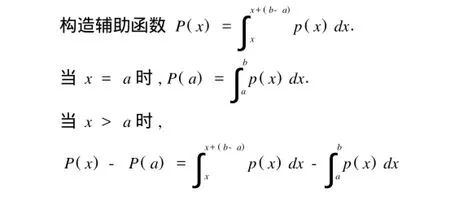



3 定理1的推廣與應用


2.Institute of Chemical Defense,Beijing 102205)

