泰勒公式與泰勒級數的異同和典型應用

鮑培文

(武警特種警察學院數理教研室,北京昌平 102211)

泰勒公式與泰勒級數的異同和典型應用

鮑培文

(武警特種警察學院數理教研室,北京昌平 102211)

以高等數學中泰勒公式、泰勒級數為基礎,探究泰勒公式與泰勒級數的區別與聯系,將一元函數的泰勒公式推廣到多元函數的泰勒公式,展現它們的一些應用,使泰勒公式與泰勒級數的內容系統化,以便于學員學習1

泰勒公式; 麥克勞林公式; 泰勒級數; 冪級數

泰勒公式是高等數學中導數應用的內容之一,在理論研究和數值計算中具有廣泛的應用,泰勒級數是函數項級數的特例,泰勒公式和泰勒級數在解決實際問題中有某些的相似性,但是它們引入不同,因此還是有一定的差異性.由于泰勒公式是通過重復運用柯西中值定理得來的,過程比較復雜,因此學員在理解泰勒公式時對最后要加上一個需要附加說明的余項感到抽象,難以接受這么一個有著附加說明,不知道ξ是什么的余項.泰勒級數屬于函數項級數中的冪級數,與泰勒公式在近似計算、極限運算、級數與廣義積分的斂散性判斷等方面有具體應用;但是學員總不會將題目和泰勒公式、泰勒級數的應用聯系在一起.在沒有理解泰勒公式、泰勒級數的前提下,寫出常見函數的泰勒公式、泰勒級數對學員來說只是一種機械行為,沒有任何意義.如何學好、用好泰勒公式和泰勒級數呢?本文努力探究泰勒公式與泰勒級數的區別與聯系,將一元函數的泰勒公式推廣到多元函數的泰勒公式,展現它們的廣泛應用,以便于學員將高等數學中泰勒公式、泰勒級數的內容系統化,為后續內容的學習打下基礎.

1 一元函數y=f(x)的泰勒公式與麥克勞林公式

1.1 一元函數y=f(x)的泰勒公式

當f(x)在含有x0的某個鄰域(a,b)內具有直到n+1階的導數,則/x∈(a,b),有

稱(1)式為f(x)按(x-x0)的冪(或在x0處)展開到n階的泰勒公式,稱(2)式為f(x)按(x-x0)的冪(或在x0處)展開的n階泰勒多項式,稱(3)式為泰勒公式的余項,也成為拉格朗日型余項.

1.2 一元函數y=f(x)的麥克勞林公式

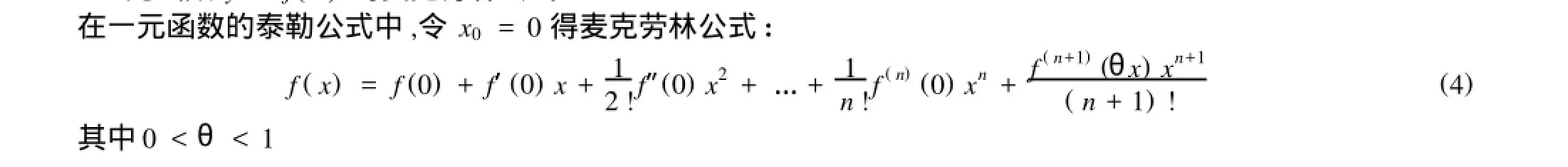
2 一元函數y=f(x)的泰勒級數與y=f(x)展成(x-x0)的冪級數

2.1 泰勒級數

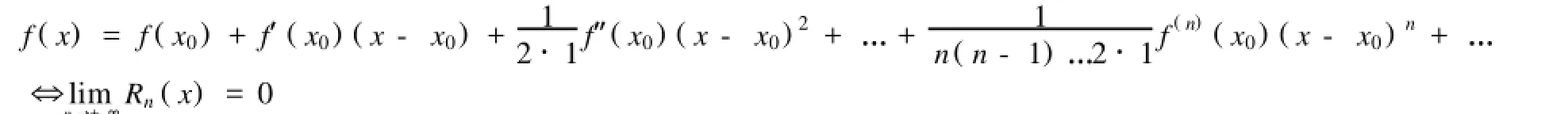
2.2 泰勒級數與泰勒公式的區別與聯系

泰勒公式中含有有限多項,泰勒級數中含有無限多項,泰勒公式不是泰勒級數,泰勒級數也不是泰勒公式1

當f(x)的各階導數都存在時,f(x)的泰勒級數在收斂情況下一定等于f(x);但不論f(x)的泰勒級數是否收斂,只要f(x)有n+1階導數,就有泰勒公式成立1可見泰勒級數收斂時,與泰勒公式結果一致,都是f(x).

2.3 f(x)展成(x-x0)的冪級數

3 二元函數z=f(x,y)的泰勒公式

4 泰勒公式與泰勒級數的應用

4.1 泰勒公式與中值定理的關系

可見,當n=0時,y=f(x)的泰勒公式變為拉格朗日中值定理,z=f(x,y)的泰勒公式正是二元函數的中值定理1

4.2 利用泰勒公式、麥克勞林公式對函數進行估值和近似計算

泰勒公式與泰勒級數有一定的聯系,如果函數可以展成泰勒級數,在收斂域內該泰勒級數與泰勒公式相等,以上泰勒公式的應用與泰勒級數的應用相通1泰勒公式與泰勒級數不僅在微分學中有重要作用,而且在積分學及線性代數的矩陣與行列式中也有一定的應用,這部分可以參看文獻[3],[4].

[1]吳建成.高等數學[Z].北京:高等教育出版社,2005.

[2]吉米多維奇.數學分析題集[Z].北京:高等教育出版社,1984.

[3]張銳,楊海成.泰勒公式在不等式和行列式中的應用[J].數學教學研究,2009,(10).

[4]熊燦.討論泰勒公式的綜合應用[J].北京電力高等專科學校學報,2009,(11).

Abstract:Based on the Taylor formula and Taylor series,the paper concludes its difference and connection,spreads Taylor formula fromfunctions of one variable to multiple functions,gives some examples of application,formthe content of Taylor formula and Taylor series into a system so that it's easy to learn.

Key words:Taylor formula; Maclaurin formula; Taylor series; power series

The Taylor Formula and Taylor Series and its Application

BAO Pei-wen
(The Professor of Department of Science,Special Police College,Beijing 102211)

O151.2

A

1671-9743(2011)02-0090-04

2010-12-14

鮑培文(1968-),女,江西南昌人,武警特警學院教授,碩士,主要研究高等數學、應用數學、軍事運籌學的教學及優化理論.