基于廣義隨機Petri網的供應鏈物流模式構建

姚丹

1 廣義隨機Petri網的建模方法

1.1 基本Petri網

Petri網是由C.A.Petri于1962年在其博士論文中提出的，經過多年發展，已逐漸成為各個學科中強有力的圖形建模與分析工具。Petri網是由位置(Places)、轉移(Transitions)和連接兩者間關系的有向弧(Directed Arcs)所組成的一種有向圖，其中，“位置”的作用是決定“轉移”能否發生，“轉移”的作用是改變系統的狀態。

一般情況下，在Petri網的圖形表示中，位置用圓圈（“○ ”）表示，轉移用直線段（“│ ”）或矩形（“□ ”)表示，位置與轉移之間的流關系用有向弧表示。

1.2 廣義隨機Petri網

早期的Petri網未引入時間概念，為了分析離散事件動態系統的時間性能指標、信息傳輸延時等，在每個變遷的可實施與實施之間聯系一個隨機的延遲時間，稱為隨機Petri網(Stochastic Petri Net，SPN)。SPN應用在系統模型的性能分析中分為三步：（1）給出系統的一個SPN模型：（2）構造出于該SPN同構的馬爾科夫鏈；（3）基于馬爾科夫鏈的穩定狀態概率進行所要求的系統性能分析，繼而可以對隨機Petri網所模擬的實際系統做各種性能的評價。但隨機Petri網的狀態空間會隨著問題的增大而呈指數增長，使隨機Petri網同構的馬爾可夫鏈難以求解。為解決這一問題，Marsan領導的科研組在1984年提出了廣義隨機Petri網理論，它是對SPN的一種擴充，它將變遷分為兩類，一類是瞬時變遷與隨機開關相關聯且實施延時為零，另一種為時間變遷與指數隨機分布的實施延時相關聯。應用廣義隨機Petri網建模的具體過程是，給出研究對象的網絡結構、構建研究對象的廣義隨機Petri網模型、構造馬爾科夫鏈計算系統性能。

假設∑=(P,T;F,M0,λ)為隨機Petri網，其中∑'=(P,T;F,M0)為一個原型Petri網，λ:T→R0；設T={t1,t2,…,tn}，則對ti∈T，λ(ti)=λi為1個非負實數，它表示變遷ti的發生速率.ti發生的時延di由于負指數分布具有無記憶特性，如果∑是1個有界的隨機Petri網，那么∑的可達標識圖RG(∑)等同于1個有限的馬爾科夫鏈（MC），該馬爾科夫鏈的狀態空間就是∑的可達標識集R（M0）。設∑=(P,T;F,M0,λ)為 1個隨機 Petri網，λ=[λ1,λ2,…，λn]，其中（n= ||T ）；R（M0）是 ∑ 的可達標識集；設 ||R(M0)=r，那么r階矩陣Q=[qij]r×r稱為∑的概率轉移矩陣，其中

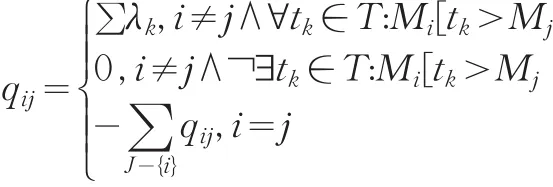
通過概率轉移矩陣，可以求出馬爾科夫鏈上的r個狀態（對應∑的r個可達標識）的穩定狀態的概率可以用一個r維向量 ∏=[π1,π2,…,πr]表示，r= ||R(M0) ，r維向量 ∏ 滿足下列方程組，其中Q是概率轉移矩陣，通過上式有r+1個方程的方程組，可以求出向量∏。

2 基于廣義隨機Petri網的供應鏈物流業務流程研究

2.1 物流業務流程

物流企業主要針對物品的流向進行操作，以此為客戶提供接貨、入庫、出貨配送、調撥、退換貨等物流業務服務，從而使生產企業專注于生產，而將產品的運輸和倉儲工作全權交給物流企業去完成，包括訂單等客戶的服務業務、運輸業務、存儲與配送業務等。圖1是以某物流企業為例列出基本的業務流程。

其中,A為接受托運申請，簽訂運輸合同；B為物流企業接受委托，發放空箱，貨物裝箱，簽發運單；C為起點站裝車，運輸；D為貨物卸車，對貨物入庫分揀；E為通知收貨人提貨，貨物交付。

物流企業通過對客戶的服務，接收到客戶的訂單需求，然后根據貨物及客戶的所在位置，選擇最佳的運輸與配送方案，將工廠所生產出的產品以最快的速度送達指定的庫存地點，最后根據貨物情況進行入庫分揀整理后，交給收貨人，整個物流業務流程結束。物流業務流程的廣義隨機Petri網模型如圖2所示。

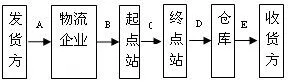
圖1 物流業務流程圖

2.2 物流業務流程簡化的廣義隨機Petri模型

按照廣義隨機Petri網的建模流程，首先構建廣義隨機Petri網模型，根據供應鏈的網絡結構以及業務流程，得到物流業務的簡化模型，如圖3所示。圖3中供應鏈的簡化GSPN反應了物流業務作業流程，它是由8個庫P和7個變遷t組成，這些變遷均為時延變遷，相應的速率分別用λ表示。其中模型中庫所、變遷所代表的含義如表1所示。

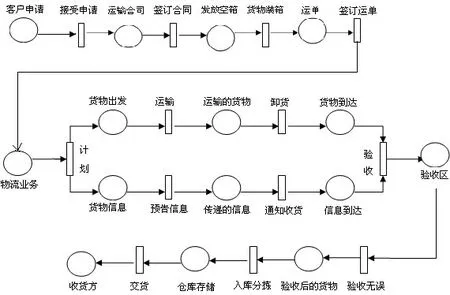
圖2 物流業務流程的廣義隨機Petri網模型示意圖

2.3 系統性能分析

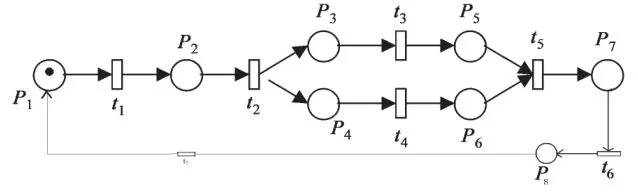
圖3 物流業務流程簡化的Petri模型

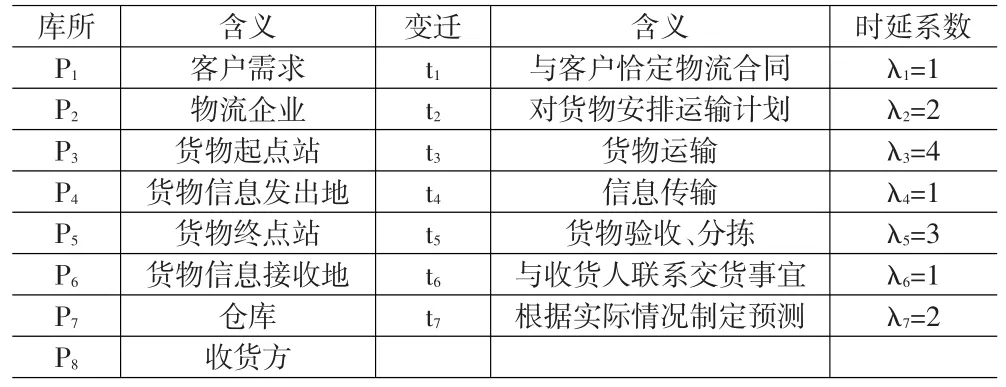
表1 物流業務流程Petri網模型元素符號設定表

由上述所給出的廣義隨機Petri網模型構造出同構的馬爾科夫鏈，根據馬爾科夫鏈的穩定狀態概率進行系統性能分析。與圖3 GSPN所對應的馬爾科夫鏈如圖4所示。表2是與之相對應的可達標識集。

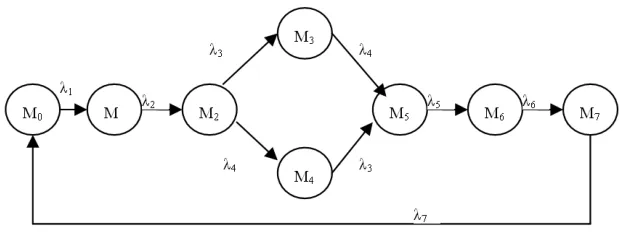
圖4 物流業務的馬爾科夫鏈

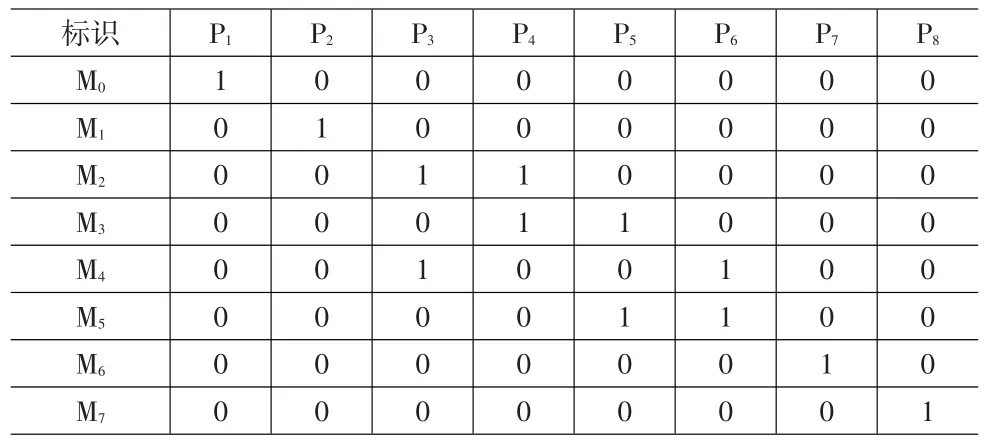
表2 GSPN中的可達標識集

可求得各標識的穩態概率值為P（M0）=0.3；P（M1）=0.3；P（M2）=0.15；P（M3）=0.0375；P（M4）=0.15；P（M5）=0.0375；P（M6）=0.0125；P（M7）=0.0125。根據穩態概率，可以對系統性能進行分析。該系統包含所有變遷，系統平均執行時間就是供應鏈的平均執行時間。則Σ′中令牌平均數=2.04；單位時間進入子系統Σ′的令牌數為λ=λ1P（M（P1）=1）=0.3，可得平均執行時間為T=N/λ=6.83（工作日）。平均執行時間T的大小反映了整個系統的組織結構運行的效率，可以通過T的大小比較不同網絡結構的運行效率狀況。

物流業務各環節的運作效率可以通過其穩定狀態下處于忙狀態的概率反映出來。令A1、A2、A3分別代表客戶服務業務、物流配送業務和倉儲管理業務，計算式為A1={M0，M1}；A2={M2,M3,M4,M5}；A3={M6,M7}。因此客戶服務占時間總比例為0.6，物流配送業務占時間總比例為0.375，倉儲管理業務所占時間比例為0.025，這些數據說明各個環節的運作效率情況。如P(A2)＞P(A3)說明了物流配送業務的效率比倉儲管理效率低，這與實際情況相符，因為配送比倉儲花費時間少導致限制時間多，效率比較低。

3 結束語

本文構建供應鏈物流業務廣義隨機Petri網模型，對物流業務流程進行模擬優化分析，為物流供應鏈的業務模式選擇提供了建模仿真的思路，可幫助物流企業動態、連續地監測內部服務質量變動情況、平均執行時間的大小和運作效率的高低，對于管理決策有一定的參考價值，對于效率較低的環節可以考慮改變管理模式以提高運作效率。本文中的供應鏈的廣義隨機Petri網是簡化模型，如何真正求解復雜的供應鏈物流業務模式系統指標，是需要進一步研究和探索的問題。

[1]Ole Mortensen,Olga W.Lemoine.Integration between Manufacturers and Third Party Logistics Providers?[J].International Journal of Operations&Production Management,2008,28(4).

[2]Kara S,Rugrungruang F,Kaebernick H.Simulation Modeling of Reverse Logistics Networks[J].International Journal of Production Economics,2007,106(1).

[3]Ilaria Giannoccaro et Pierpaolo Pontrandolfo.Supply Chain Coordination by Revenue Sharing Contracts[J].International Jjournal of Production Economics，2004，89(2).

[4]王玉燕,李幫義,申亮.TPT-CLSC的協調研究[J].中國管理科學,2007,15(5).

[5]謝楠，李愛平，徐立云.基于廣義隨機Petri網的可重組制造單元建模與分析方法[J].計算機集成制造系統，2006，12（6）.

[6]王冬冬，達慶利.基于模糊Petri網的供應鏈牛鞭效應的成因與控制分析[J].系統管理學報，2007,16(1).

[7]夏訓嘉.現代物流企業知識管理策略研究[J].中國流通經濟,2008，(8).