批量生產(chǎn)作業(yè)車間的雙資源多目標調(diào)度問題研究

初紅艷 費仁元 李風(fēng)光 鄧穎輝

(北京工業(yè)大學(xué)機電學(xué)院，北京100124)

車間批量調(diào)度在先進制造系統(tǒng)的生產(chǎn)實際中具有非常高的普遍性，研究車間批量調(diào)度的優(yōu)化方法，不僅可以促進調(diào)度理論的發(fā)展，而且對于企業(yè)提高生產(chǎn)效率和生產(chǎn)能力，降低生產(chǎn)成本有著重要的影響［1］;雙資源調(diào)度是指在調(diào)度過程中不僅考慮加工設(shè)備受到制約的情況，而且要考慮有著熟練加工能力或特殊加工能力的工人，工人和設(shè)備的合理利用明顯有利于提高產(chǎn)品的綜合效益;多目標調(diào)度則是指在作業(yè)車間內(nèi)將各工件的工序合理安排在設(shè)備上，并確定各工序的開工時間，同時優(yōu)化給定的多個性能指標。

通過對實際生產(chǎn)狀況的分析，針對作業(yè)車間批量生產(chǎn)的問題提出了分批調(diào)度策略。建立雙資源多目標優(yōu)化調(diào)度模型，對分批后的工件采用遺傳算法和禁忌搜索算法相結(jié)合的混合優(yōu)化算法進行調(diào)度。調(diào)度算例驗證了研究的可行性和有效性，對生產(chǎn)實踐具有一定的指導(dǎo)作用。

1 分批調(diào)度策略

分批的核心思想是:當(dāng)車間只加工一類工件時，必定存在一個最優(yōu)的分批方案。

先確定一定數(shù)量某種工件單獨加工時應(yīng)該劃分的子批數(shù)，然后計算每個子批包含的工件數(shù)，計算每個子批的每道工序需要的新的加工時間，并將每個子批看做一個新工件。在此基礎(chǔ)上采用調(diào)度算法進行調(diào)度。

某工件單獨加工時，需要劃分的批次判定公式為

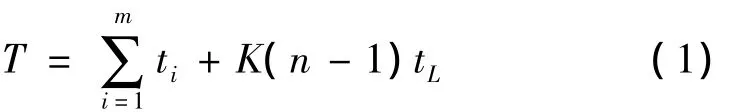
式中:m為工序數(shù);n為批數(shù);ti為該工件第i工序的加工時間;tL為最長工序的加工時間;K為子批中包含的工件數(shù)(此時判定公式并不是求得最終結(jié)果的公式，K根據(jù)計算結(jié)果能取非整數(shù))，T為考慮分批的時間參數(shù)。

進行分批時，依次取n=1，2，…，N(N為工件的數(shù)目)，根據(jù)式(1)計算此時的時間參數(shù)T，比較找出最小的T，輸出與其對應(yīng)的分批數(shù)n。

分批算法中引入了參數(shù)K，可以取為非整數(shù)，這樣就豐富了分批的情況，而不僅僅局限于完全等分批。比如，10個工件，可以分成4個子批，每個子批包含工件數(shù)為2，2，3，3。這樣會比完全等分批更有可能得到最優(yōu)解。另外，該算法是確定了合理的分批數(shù)目之后再進行子批相關(guān)數(shù)據(jù)的計算，相比于計算每次分批之后的子批數(shù)據(jù)，大大減小了計算任務(wù)。

2 雙資源多目標調(diào)度算法

遺傳算法經(jīng)常被用于解決車間調(diào)度問題，經(jīng)典的遺傳算法雖然具有較好的全局優(yōu)化求解能力，但當(dāng)出現(xiàn)適應(yīng)度很大的超常個體時，容易引起早熟收斂;而禁忌搜索算法通過引入禁忌表，避免迂回搜索，局部搜索能力強，彌補了遺傳算法的不足。

本文利用遺傳算法良好的全局搜索能力和禁忌搜索算法具有記憶能力的局部優(yōu)化特性，將兩種算法進行混合［2］，用于解決雙資源多目標車間調(diào)度問題。先用遺傳算法進行全局搜索，通過遺傳操作，改善種群質(zhì)量，再以該種群作為禁忌搜索算法的初始解，用禁忌搜索算法進行局部搜索，以在算法的全局收斂性能和避免早熟收斂方面有較大改善。

2．1 算法描述

算法流程如下:

Step 1:給定初始參數(shù)(包括最大迭代次數(shù)Y，群體規(guī)模s，交叉概率Pc和變異概率Pm);

Step 2:按照給定編碼方式編碼，產(chǎn)生初始群體，其中有s個染色體;

Step 3:按照給定的解碼方式解碼，得到每個個體的各優(yōu)化指標，包括生產(chǎn)周期T1，T2，…，Ts，工件總延誤時間d1，d2，…，ds，設(shè)備閑置時間e1，e2，…，es和工人閑置時間w1，w2，…，ws;

Step 4:按照多目標決策理論計算群體中每個個體的適應(yīng)度值f(x1)，f(x2)，…，f(xs);

Step 5:調(diào)用TS搜索過程，對群體中的每一個個體進行局部搜索，從群體中選擇r個較優(yōu)解添加到禁忌表中作為禁忌對象。記各禁忌對象未被選擇的次數(shù)為Li(i=1，2，…，r)，如果Li大于禁忌長度L，將所對應(yīng)個體釋放，轉(zhuǎn)Step 6;否則直接轉(zhuǎn)Step 6;

Step 6:根據(jù)交叉概率和變異概率對種群進行交叉、變異遺傳操作，得到新種群;

Step 7:如果循環(huán)次數(shù)y＜Y，令y=y+1，轉(zhuǎn)Step 3;否則轉(zhuǎn)Step 8;

Step 8:停止運算，從禁忌表中選擇確定數(shù)量的非劣解;

Step 9:使用層次分析法從非劣解集合中選擇較優(yōu)解作為最終的調(diào)度方案。

2.2 遺傳編碼

采用基于工序的編碼方式。給同一工件的所有工序指定相同的符號，再根據(jù)它們在染色體中出現(xiàn)的順序進行解釋。例如，對于n個工件，每個工件有m道工序的問題，每個染色體由n×m個代表工序的基因組成，每個工件出現(xiàn)在染色體中m次。

以1個3工件，每個工件3道工序的問題為例，染色體的表達形式為211122333，其中第一個2表示工件2的第1道工序，第二個1表示工件1的第2道工序。

2．3 解碼

解碼即對編碼進行翻譯，產(chǎn)生具體可操作的工序安排方案。具體解碼過程是:

(1)假設(shè)所有工序的理想可被加工起始時刻:設(shè)備k可以使用的時刻Mk=0(k=1，2，…，m)，工人w可以使用的時刻Pw=0(w=1，2，…，p)，工件i的第一道工序可被加工時刻Ti1=0(i=1，2，…，n);

(2)從工序集合S中取出此刻排在第一位未被調(diào)度的工序Oij(工件i的第j道工序)，從能加工工序Oij的設(shè)備集合中挑選最先空閑的設(shè)備k，其可以使用的時刻為Mk，從能操作設(shè)備k的工人集合中挑選最先空閑的工人w，其可以工作的最早時間為Pw;

(3)工序Oij開始加工時刻Tb=max(Mk，Pw，Tij)，得到工序Oij的完工時刻fij=Tb+tij，其中Tij為工件i的第j道工序可被加工的時刻，tij為加工工序Oij所需的時間;

(4)如果j=Ji，則工件i的完工時間Fi=fij，否則Ti(j+1)=fij，且Mk=fij，Pw=fij，其中j=1，2，…，Ji，Ji為工件i的工序總數(shù);

(5)檢查工序集合S中是否還有未被調(diào)度的工序，如有，轉(zhuǎn)(2)，否則，生產(chǎn)周期T=max(Fi)。

2．4 遺傳操作

(1)選擇 本研究通過禁忌搜索算法保留相對優(yōu)秀的個體，因此選擇操作將各個解的適應(yīng)度值按順序排列即可。

(2)交叉 采用循環(huán)交叉操作。循環(huán)交叉操作是將另一個父代個體作為參照，以對當(dāng)前父代個體中的基因位置進行重組［3］。

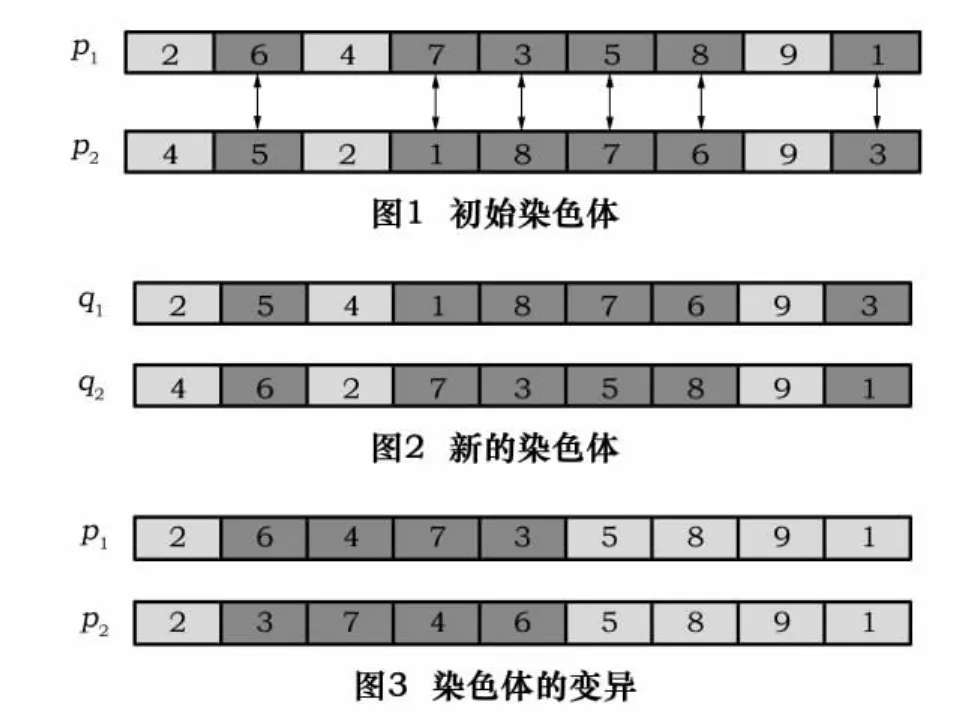
例如，給定2個染色體p1，p2，如圖1所示。隨機選擇一個操作位置，如第2個位置，其對應(yīng)的基因為6和5，則交叉過程為:首先選擇循環(huán)鏈6-5，5-7，7-1，1-3，3-8，8-6，如圖 1 所示。對應(yīng)位置的基因交換后，生成新個體q1，q2，如圖2所示。

(3)變異 采用逆轉(zhuǎn)變異法，即在染色體中隨機選擇兩點，然后將兩點間的基因以逆向排序插入到原位置中。如給定一個染色體p1，假設(shè)選中2號、5號位置，則變異后的染色體為q1，如圖3所示。

2．5 禁忌搜索算法參數(shù)確定

(1)禁忌對象和候選解的確定 以遺傳操作后得到的種群作為禁忌搜索算法的候選解。禁忌對象是指那些被置入禁忌表中的變化元素，禁忌的目的是為了盡量避免迂回搜索。本算法將候選解中最優(yōu)的40%作為禁忌對象，置入禁忌表中。

(2)禁忌長度的確定 禁忌長度是禁忌對象在不考慮藐視準則的情況下允許未被選取的最大次數(shù)。禁忌長度根據(jù)不同的初始種群大小依據(jù)經(jīng)驗選取不同值。本文中禁忌長度隨著種群規(guī)模的增大而增大。當(dāng)某禁忌對象未被選取的次數(shù)達到禁忌長度值時，將該禁忌對象相對應(yīng)的染色體釋放，參與遺傳操作，以避免產(chǎn)生局部最優(yōu)。

3 多目標決策理論在算法中的應(yīng)用

多目標決策理論的基本問題是研究如何在有多個相互沖突的決策準則(因素、目標、目的)下進行科學(xué)和有效地決策。層次分析法是20世紀70年代由美國學(xué)者薩蒂提出的一種多目標評價決策方法。其基本思路是決策者將復(fù)雜問題分解為若干層次和若干要素，在各要素間進行簡單的比較、判斷和計算，以獲得不同要素和不同待選方案的權(quán)重，從而為選擇最優(yōu)方案提供決策依據(jù)。

在多目標車間調(diào)度問題中利用多目標決策理論，首先要確定各個目標的權(quán)重系數(shù)，然后對各個優(yōu)化目標做無量綱化處理，確定目標函數(shù)。最后再根據(jù)層次分析法由非劣解集合求出較優(yōu)解。

3．1 計算各目標權(quán)重系數(shù)

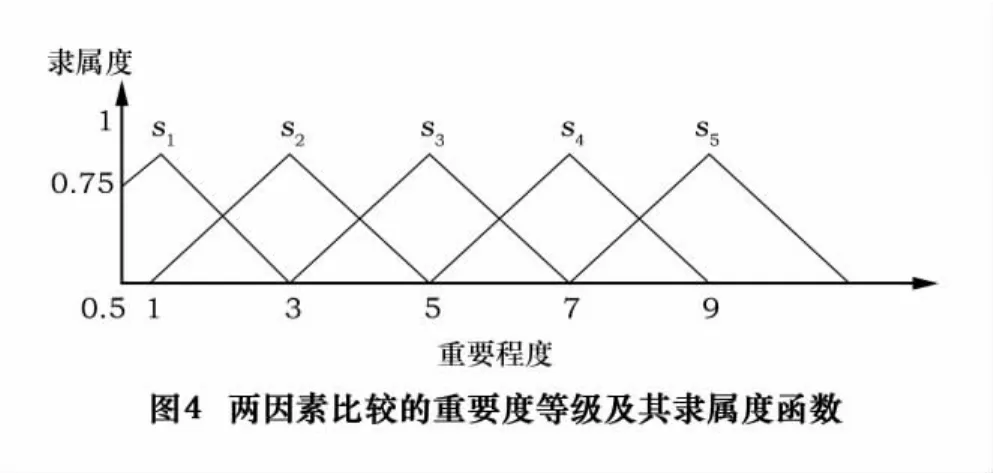
根據(jù)生產(chǎn)車間的具體情況，確定目標之間的相對重要性。目標比較的尺度分為5個等級:同樣重要、稍微重要、明顯重要、強烈重要與極端重要。對應(yīng)的隸屬函數(shù)分別為s1、s2、s3、s4、s5，如圖 4 所示。

本研究的車間調(diào)度問題中，優(yōu)化目標為生產(chǎn)周期、工件總延誤時間、設(shè)備閑置時間和工人閑置時間。對這些目標兩兩比較，重要性較小的數(shù)為1。

假設(shè)根據(jù)生產(chǎn)需要，確定各個目標重要程度如表1所示。以重要度級別的隸屬度函數(shù)作為隨機數(shù)的概率密度函數(shù)，按照概率分布產(chǎn)生隨機數(shù)分別代替重要度級別，得到目標比較矩陣表2。

把目標比較矩陣表2的每一元素除以其相應(yīng)列所有元素的總和，得到標準兩兩比較矩陣，根據(jù)對比平均法［4-5］，再把標準兩兩比較矩陣各行元素相加并取平均值得到各目標的權(quán)重:生產(chǎn)周期權(quán)重ω1=0.374 3，工件總延誤時間權(quán)重ω2=0.284 1，設(shè)備閑置時間權(quán)重ω3=0.189 7，工人閑置時間權(quán)重ω4=0.151 9。

表1 目標比較矩陣

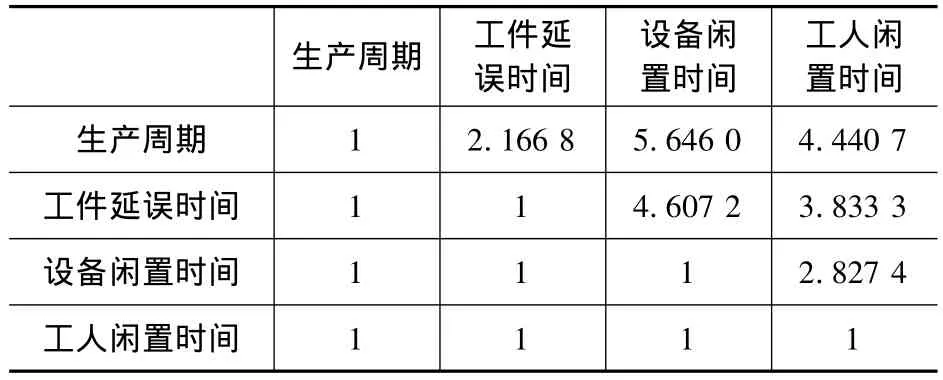
表2 用隨機數(shù)代替重要度級別得到的目標比較矩陣

3．2 計算目標函數(shù)值

在車間調(diào)度問題中，計算各指標值后，為把多個指標值集合成作為調(diào)度結(jié)果衡量標準的函數(shù)，需要對調(diào)度方案的各指標值按下列公式進行無量綱標準化處理:

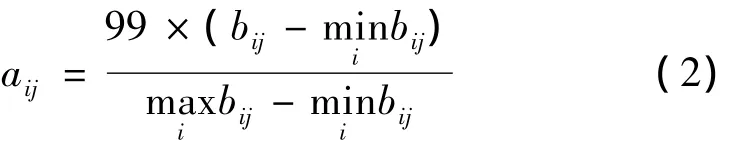
標準化處理后，一個調(diào)度結(jié)果所對應(yīng)的生產(chǎn)周期，工件總延遲時間，設(shè)備閑置時間和工人閑置時間分別表示為f1(x)、f2(x)、f3(x)、f4(x)，f(x)為衡量調(diào)度結(jié)果綜合指標的目標函數(shù)，因為各單項指標均是求極小值，則按照線性加權(quán)和方法得到目標函數(shù)為:

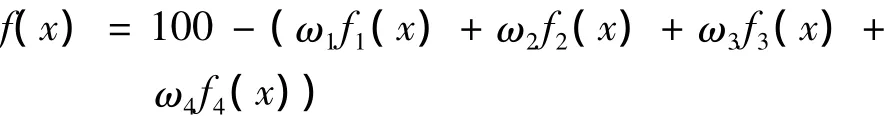
此目標函數(shù)即為遺傳算法的適應(yīng)度函數(shù)。

3．3 獲得非劣解集合和較優(yōu)解

在優(yōu)化算法的計算過程中，可以獲得和保留非劣解。本文采用禁忌搜索算法實現(xiàn)。

獲得非劣解集合后，根據(jù)層次分析法由非劣解集合中獲得較優(yōu)解。

根據(jù)目標比較矩陣表1，按照1-5標度法生成層次分析法的層次比較矩陣表3，然后把層次比較矩陣表3的每一元素除以其相應(yīng)列所有元素的總和，得到標準兩兩比較矩陣，再把標準兩兩比較矩陣各行元素相加并取平均值就得到各目標的權(quán)重:生產(chǎn)周期權(quán)重ω1=0.449 5，工件延誤時間權(quán)重ω2=0.259 6，設(shè)備閑置時間權(quán)重 ω3=0.170 7，工人閑置時間權(quán)重 ω4=0.120 2。則各個目標權(quán)重系數(shù)矩陣為U=［0.449 5 0.259 6 0.170 7 0.120 2］T。

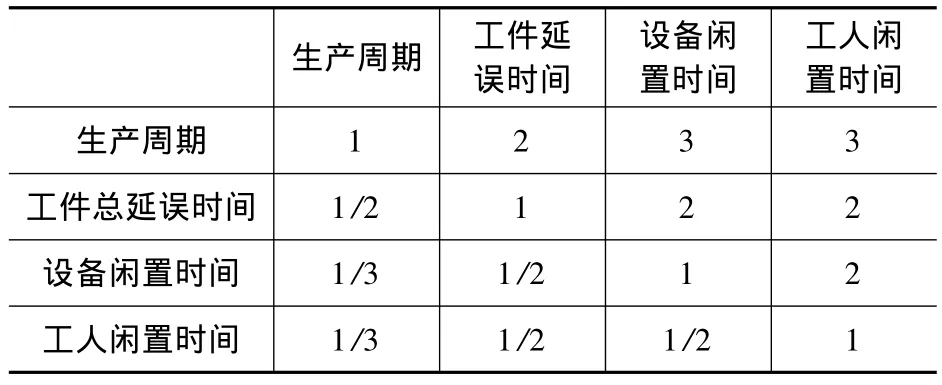
表3 層次比較矩陣

假設(shè)得到5個非劣解如表4所示。

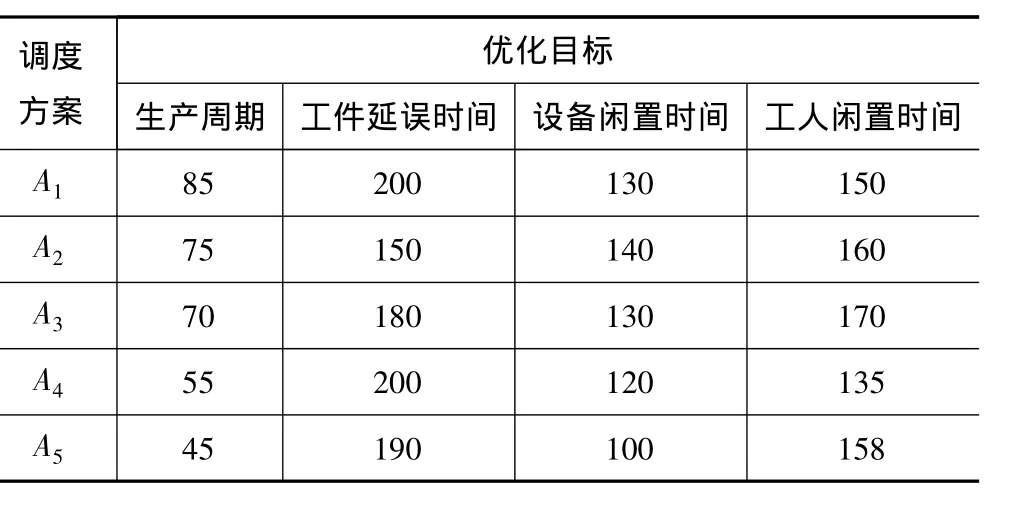
表4 非劣解集合

生產(chǎn)周期指標設(shè)為G1，為逆向指標，即生產(chǎn)周期越大，方案越不利，因此建立判斷矩陣得表5。

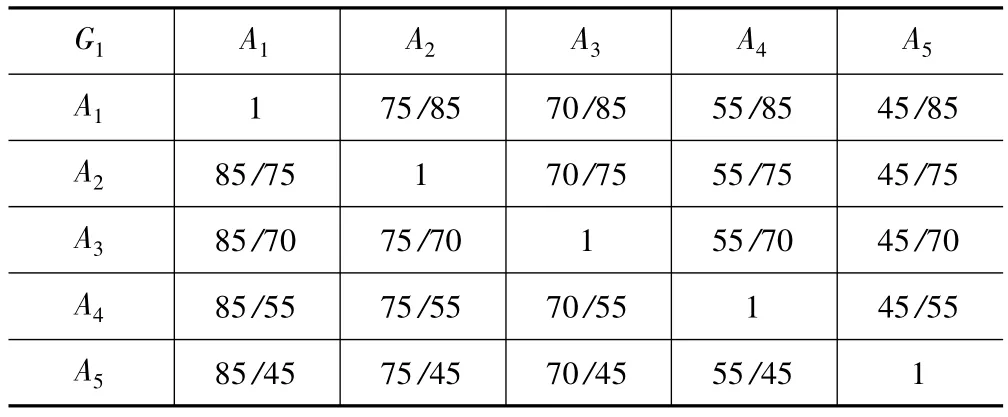
表5 生產(chǎn)周期判斷矩陣

由于本文所涉及的每個優(yōu)化目標都為逆向指標，可按照同樣的方法計算各調(diào)度方案中其他優(yōu)化指標的權(quán)重值。

工件延誤時間權(quán)重:

設(shè)備閑置時間權(quán)重:

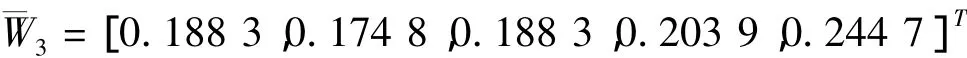
工人閑置時間權(quán)重:

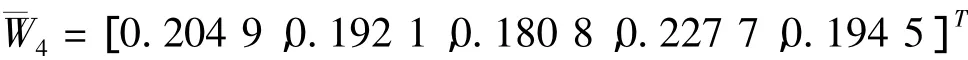
則層次總排序為:

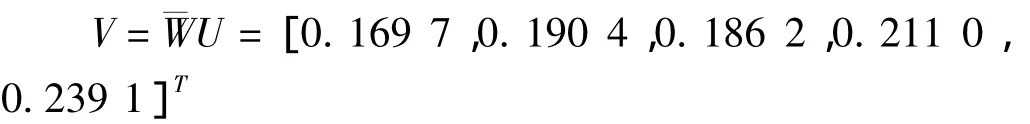
故方案的優(yōu)劣排序為:A5＞A4＞A2＞A3＞A1，A5為最優(yōu)方案。需要指出的是，如果目標權(quán)重系數(shù)矩陣U不一樣，方案的優(yōu)劣排序也會隨之變化。

4 調(diào)度算例

假設(shè)有4種工件要被加工，每種工件分別有4道工序。每道工序?qū)?yīng)的加工時間、可用設(shè)備，以及每臺設(shè)備所對應(yīng)的可操作工人如表6，表7，表8。

混合優(yōu)化算法參數(shù)設(shè)置為:初始種群規(guī)模大小為100，交叉概率0.8，變異概率0.11，禁忌表長度為40，禁忌長度為6。目標比較矩陣如表1。

表6 工序加工時間表 min

表7 工序可用設(shè)備表

表8 各設(shè)備對應(yīng)可操作工人表

4.1 加工數(shù)量為10的4×4調(diào)度

4.1.1 不分批時的調(diào)度結(jié)果

在不分批情況下，把每一種工件作為一個工件進行調(diào)度，每道工序的加工時間為單件加工時該工序加工時間與加工數(shù)量的乘積。

運用混合優(yōu)化算法的調(diào)度結(jié)果如圖5所示。

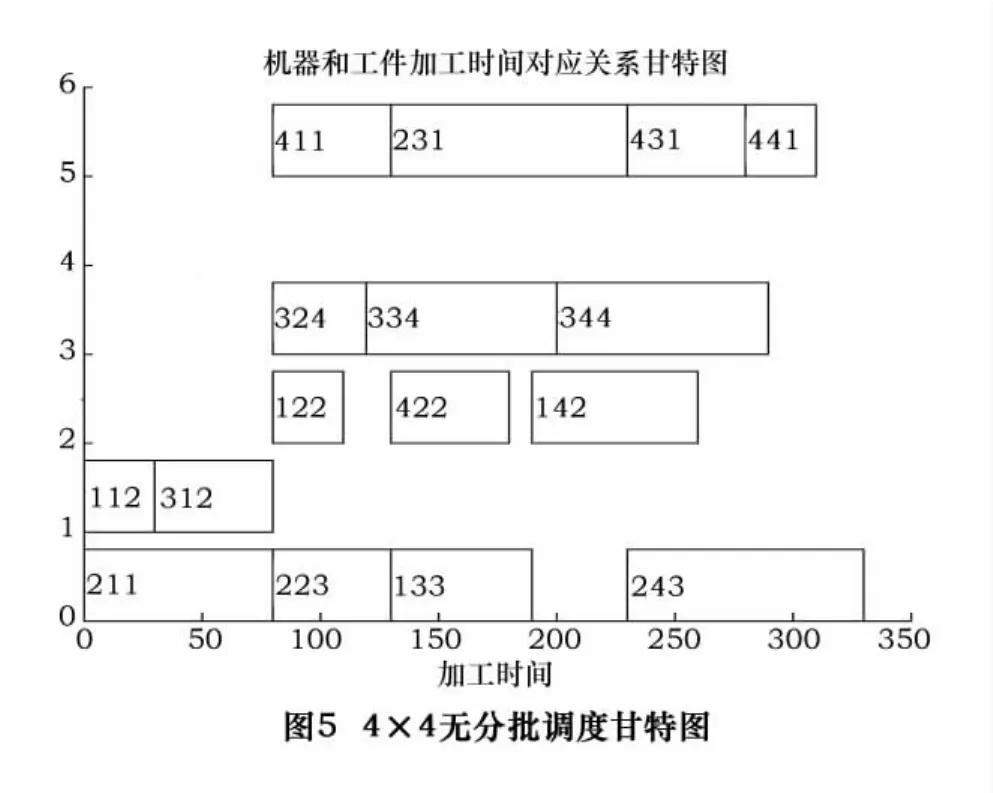
圖5中，橫軸為加工時間，縱軸為設(shè)備編號。圖中的3位數(shù)字，第1位表示工件，第2位表示該工件的某道工序，第3位表示所用加工工人。例如，圖中211表示第2個工件的第1道工序由工人1來加工，由圖可看出，該工序所用設(shè)備為設(shè)備1。

由圖5可知，在不分批情況下，該批工件加工耗時在332 min。

4.1.2 分批調(diào)度結(jié)果

采用前述的分批調(diào)度策略進行調(diào)度，可將加工數(shù)量為10的該調(diào)度問題分批為如下結(jié)果:

矩陣每一行表示一種工件，每一行的列數(shù)表示工件分成的批數(shù)，每列對應(yīng)的數(shù)字就是每批包含的工件數(shù)目。例如，第1種工件被分為4個批次，每批包含的工件數(shù)目分別為 2、2、3、3。

調(diào)度前首先進行新的加工時間的計算，把每批包含的工件數(shù)目乘以相應(yīng)的單件加工時間即可，然后把每批工件當(dāng)成一個新的工件，對其進行新的編號，從工件1到工件16，最后采用混合優(yōu)化算法進行調(diào)度。

調(diào)度結(jié)果表明，在分批調(diào)度的情況下最終加工耗時在267 min左右，與不分批情況下的332 min相比，共節(jié)約65 min，占總加工時間的19.6%。

4.2 加工數(shù)量為30的4×4調(diào)度

增加每種工件的加工數(shù)目為30，其他條件不變，采用分批策略得分批結(jié)果如下:

采用混合優(yōu)化算法進行調(diào)度后，得加工時間為785 min。而在不分批情況下，加工耗時在983 min，共節(jié)約198 min，占總加工時間的20.1%。

5 結(jié)語

對批量生產(chǎn)作業(yè)車間的雙資源多目標調(diào)度問題進行了研究，結(jié)論如下:

(1)采用的分批策略能大幅縮短生產(chǎn)周期，充分利用人力和設(shè)備資源;

(2)采用遺傳算法和禁忌搜索算法相結(jié)合的混合優(yōu)化算法，進行雙資源多目標車間的調(diào)度，在優(yōu)化效率和優(yōu)化速度上都得到很大的提高和改善;

(3)多目標決策理論引入到混合優(yōu)化算法中，用于適應(yīng)度函數(shù)的計算及較優(yōu)解的獲得，很好地解決了多個優(yōu)化目標下，綜合最優(yōu)調(diào)度方案的獲得。

［1］劉冉.批量生產(chǎn)企業(yè)的車間計劃調(diào)度系統(tǒng)設(shè)計與開發(fā)［D］.西安:西北工業(yè)大學(xué)，2005.

［2］梁迪，謝里陽，隋天中，等.基于遺傳和禁忌搜索算法求解雙資源車間調(diào)度問題［J］.東北大學(xué)學(xué)報，2006，27(8):895-898.

［3］Hisao T，Shinta M，Hideo T.Modified simulated annealing algorithms for the flowshop sequencing［J］.Euro J of Operation Research，1995，21(9):388-398.

［4］王竹卿.基于遺傳算法的車間調(diào)度問題研究［D］.大連:大連理工大學(xué)，2006:30-40.

［5］熊銳，蔣小壓.層次分析法在多目標決策中的應(yīng)用［J］.南京航空航天大學(xué)學(xué)報，1994，26(4):282-388.

［6］趙煥臣，許樹柏，和金生.層次分析法［M］.北京:科學(xué)出版社，1986:10-25.