隱性知識網絡傳播行為模型構建及仿真

曹 征，孫 虹

（1.中南大學 公共衛生學院，長沙 410078；2.中南大學 湘雅醫院，長沙 410008）

隱性知識網絡傳播行為模型構建及仿真

曹 征1，孫 虹2

（1.中南大學 公共衛生學院，長沙 410078；2.中南大學 湘雅醫院，長沙 410008）

隱性知識一般通過工作經驗、技藝、組織文化等方式在工作人員的頭腦中留有深刻的印象，并通過工作人員在工作中的實踐而得以表現。隱性知識的傳播網絡存在不對稱現象，它是由許多的個體所組成。一般來說，網絡密度，出度、入度中心勢，中介中心勢等是衡量隱性知識網絡不對稱的重要指標，這些指標對隱性知識傳播網絡的反映也各有不同。文章通過平均場理論分析了隱性知識傳播行為，構建起隱性知識網絡傳播模型，并對該模型進行了計算機數值仿真。

隱性知識；網絡傳播；行為分析

1 隱性知識的傳播

隱性知識是一種在長期的實踐中通過不斷地積累總結而產生的、不易通過言辭表達、不易傳播與共享的帶有個性色彩濃厚的實踐經驗性知識，它是植根于人們在工作生活中的一些觀察、經驗與頓悟所得，往往以經驗、技巧、感覺、觀察能力、特長、思維模式、價值觀、組織文化等形式表現出來。

在隱性知識傳播過程的研究中，不同的學者進行了不同的研究，日本學者 Nonaka和Takeuhci(1995)提出的知識螺旋模式最為著名[7，8,9],闡述了知識轉換的過程為社會化→外化→結合→內化→社會化→外化→ …，在顯性知識與隱性知識持續的循環轉換中不斷進行新的知識創造。Hedlund(1994)提出了通過顯性與隱性知識在個體、集體、組織和組織間相互傳播的一個知識交換模型。Eriksson和Dickson(2000)闡述了由IT基礎設施、推動者、知識傳播流程以及組織價值觀、規范與程序這四個影響因子構成的一個知識傳播與創造的模型。單雪韓(2003)提出，知識傳播者的知識外化與知識接受者的知識內化構成了整個知識的傳播過程。譚大鵬與霍國慶 (2006)在總結前人的研究后，提出了三個知識傳播過程階段，也就是準備、傳遞與整合三個階段，并且他們還創建了一般知識傳播模式[11，12]。

從信息傳播角度，Hendriks(1999)指出知識的特性決定了其不可以像商品那樣自由傳播，知識接受者在接受知識的時候也要知道如何重建知識，知識接受者必須有能力在學習的同時還要能傳播知識。Jim Botkin(2000)提出知識傳播的發送方與接受方必須要有聯系才能實現知識的傳播；所以說知識傳播就是兩個事物之間的聯系與傳播，這兩個事物可以是個體與個體，可以是個體與組織，也可以是組織之間。Connelly和Kelloway(2003)認為信息在兩者間交換或者是幫助對方的行為的匯集就是知識傳播[7，8,11]。

2 隱性知識網絡傳播過程

隱性知識傳播網絡是由若干個個體組成的網絡，如果個體A向B傳播知識，但B個體不一定向A傳播知識，這樣，可以說這種傳播網絡是非對稱的[10]。網絡傳播節點由諸多個體組成，它們相互間的聯結就構成了多種網絡聯系，各種知識就可以通過這些聯系進行傳播。一般來說，出度、入度中心勢，網絡密度，中介中心勢等是衡量隱性知識網絡不對稱的重要指標，而這些指標對隱性知識傳播網絡的反映也各有不同：

（1）網絡密度是衡量網絡節點間緊密程度的重要指標，L/[N（N-1）]是其計算公式，N和L分別代表網絡節點數以及網絡中弧的條數。在知識網絡傳播中，如果一個組織的人際網絡密度太高，將會降低組織的網絡傳播的效率，從而浪費較多的精力，進而超出預期維護的成本；反過來，如果一個組織的人際網絡密度太低，則表示人們之間的關系不密切，這樣也不利于提高知識傳播與共享的效率。

（2）就網絡節點的出入度中心勢問題而言。鑒于網絡存在知識的不對稱性，這必然導致每個節點在網絡中傳播截然不同，是否能精確計算每個節點的出入度中心勢是解決問題成敗的關鍵。多個節點的聯結進而生成了組織隱性知識傳播的網絡，隱性知識傳播效率的高低與節點的行為特性息息相關。我們可以通過節點的出入度中心勢反映每個節點與其他節點之間的直接聯系。節點出度可以表示為其代表節點vi對其他節點傳播影響的程度。其值俞大，說明vi節點向其他節點傳播的知識愈多，該節點地位愈高，所起的作用也愈大；節點入度可表示為：其代表節點vj吸收其他節點知識個體數量的多少，同樣可以得出其值愈大，吸收其他節點知識的能力愈強的結論。

基于上述的分析，在整個隱性知識傳播網絡中，其出入度中心勢的計算公式如下：

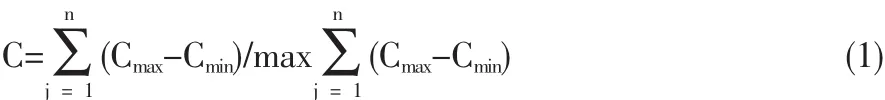
其中V(i)理解為第i個節點的出入度值，Cmax為所有節點出入度的峰值。

（3）當網絡中的某個節點置身與其他的節點之間時，為了更好地反映網絡中個人成員在整個不對稱隱性知識網絡傳播過程中自身的狀況，一個新的概率—中介中心勢必須作解釋，其公式如下：

其中，經過i-j節點的所有路徑總量用gik表示；在gij中，其經過k節點的路徑的總量用gikj表示。

3 隱性知識網絡傳播模型

本文借鑒研究文獻[1,2,3,4,5]對傳染病的研究成果，構建了隱性知識網絡傳播的傳染性模型，通過計算機模擬仿真證明了該模型。我們假定隱性知識網絡傳播的網絡在一定時點上的節點數不變，并且假定可以把網絡節點分為隱性知識易感S，隱性知識潛伏E，隱性知識傳播I，和隱性知識隔離Q四種狀態，定義時刻時各狀態節點所占的比例為S(t)，E(t),I(t),Q(t)并進一步約定ρ1,ρ2分別表示隱性知識潛伏類和隱性知識傳播的傳染率，ε表示隱性知識潛伏類成為隱性知識傳播的比例；γ為隱性知識隔離率，δ為隱性知識恢復率，即由隱性知識隔離類又成為隱性知識易感類的比率。 其中 ρ1,ρ2,ε,γ,δ 均為正常數[11,12]。

對于均勻網絡，度高度峰化，度擾動很小，近似為平均度，即 ki≈，如圖 1所示，根據平均場理論[11,12]，得出隱性知識SEIQ模型的傳播動力學方程如所示:

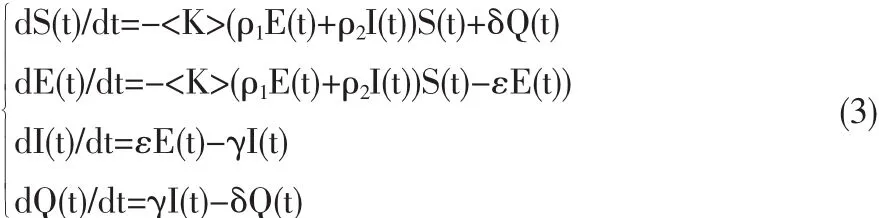
利用歸一化條件S(t)+E(t)+I(t)+Q(t)=1，代入(3)，消去S(t)，則系統可歸結為下列三維模型：

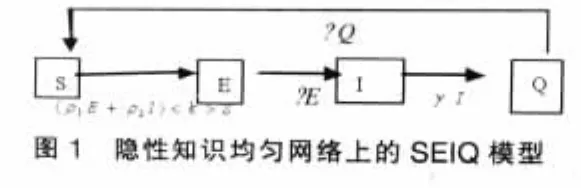
可以得出，D是系統(4)的正向不變集，隱性知識網絡傳播系統(4)的零點是其平衡點，故系統(3)有平衡點(1,0,0,0)，該平衡點可以為系統(3)的隱性知識網絡傳播平衡點。

現在我們尋求系統(3)在D內的其他平衡點，令系統(4)的右端等于零，用I表示所有其它變量，則有：

其中 ρ=(ρ1E(t)+ρ2I(t))，所以 I(t)+γ/ρI(t)+γ/εI(t)+γ/δI(t)=1

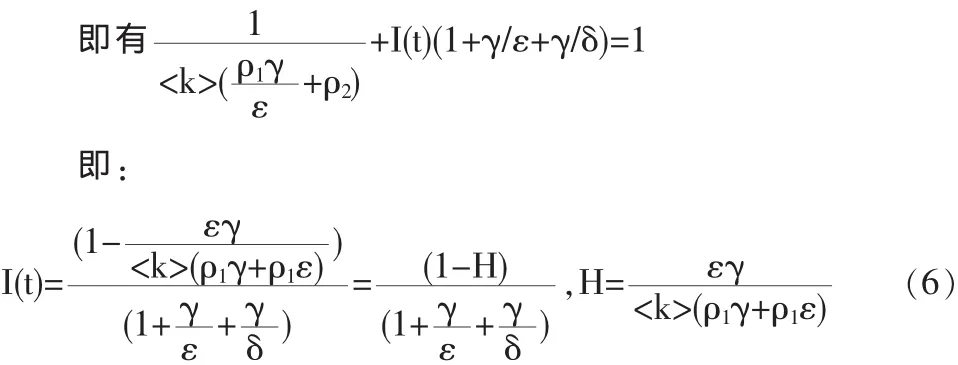
可見，當H<1時，系統（3）在內存在唯一的正平衡點(S*,E*,I*,Q*)，其中 S*,E*,I*,Q* 分別由（5）（6）兩式給出，當 H≥1時，系統（3）只有唯一平衡點(1,0,0,0)，不存在正平衡點，這里H=1的即為我們關心的隱性知識網絡傳播閾值。

4 隱性知識網絡傳播系統平衡點的穩定性討論

由于系統（3）的隱性知識網絡無效傳播平衡點，與系統（4）的零平衡點想對應，因此，只需將系統（4）的零平衡點的穩定性考慮在內即可[11,12]，我們有如下引理：

引理 1：平衡點(S,E,I,Q)=(1,0,0,0)是系統(1)的局部穩定解，記，當 H≥1 時，系統（3）收斂于(1,0,0,0)，稱其為隱性知識網絡無效傳播平衡點。

將系統（4）的右端在原點線性展開，容易得到其特征方程的三個特征根均具有負實部，故由Routh-Hurwits判斷[6]，即知零平衡點是局部漸進穩定的，即當H≥1時，系統(1)收斂于(1,0,0,0)，即隱性知識網絡無效傳播平衡點。

引理2:平衡點(S,E,I,Q)=(S*,E*,I*,Q*)是系統(1)的局部穩定解，當H<1時，系統(1)收斂于該平衡點，稱為隱性知識網絡有效傳播平衡點。

證明:對于 H<1時，系統(1)的平衡點為(S*,E*,I*,Q*)，在

該矩陣的特征值由下列的3次特征方程[11,12]

由Routh-Hurwits判斷[6]，則方程（7）的所有特征根均具有負實部，這就證明了隱性知識網絡有效傳播平衡點是局部漸進穩定的，即當H<1時，系統(1)收斂于(S*,E*,I*,Q*)。

5 隱性知識網絡傳播傳染曲線仿真

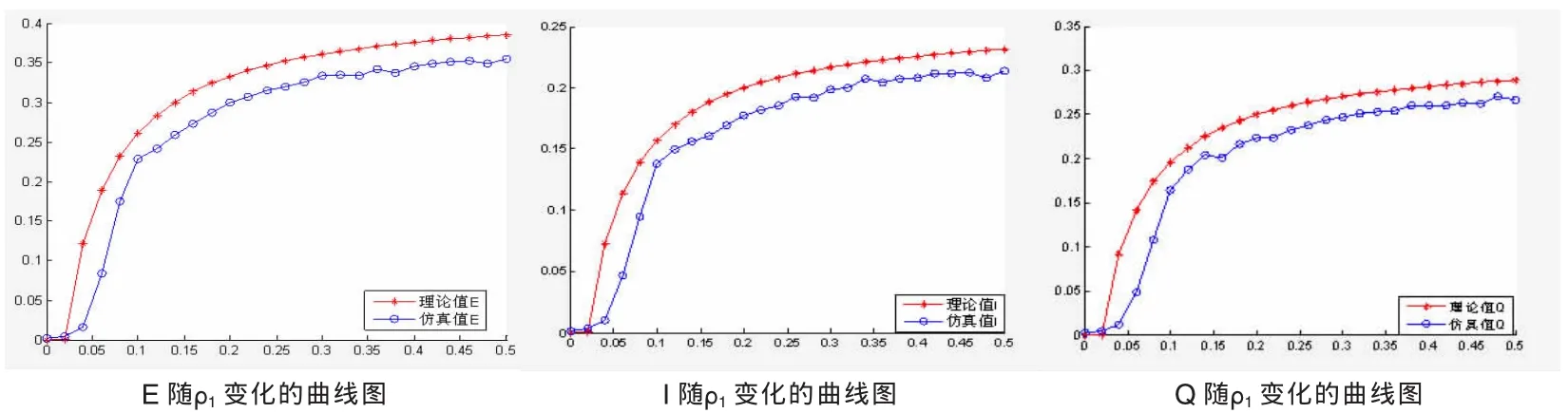
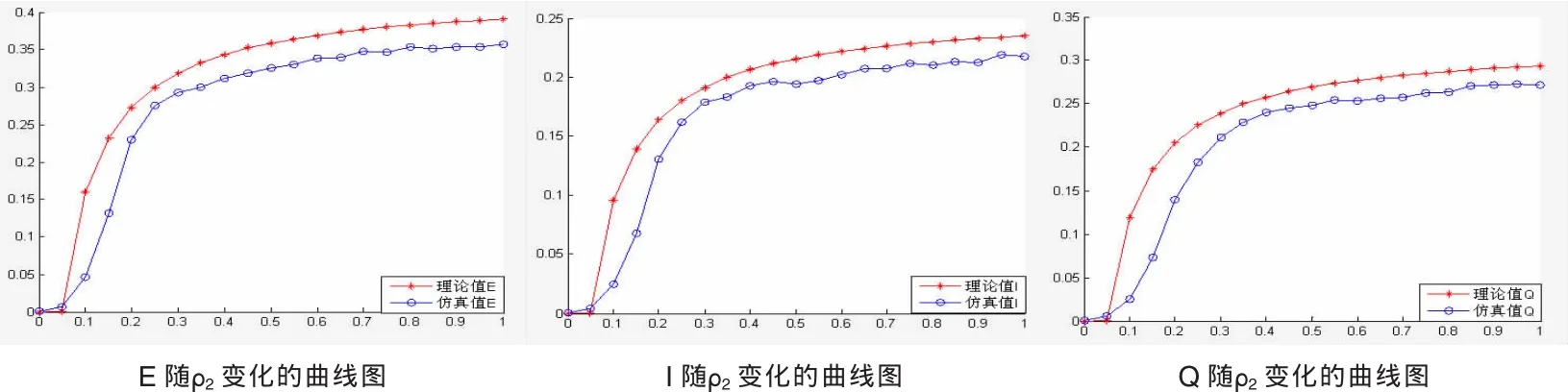
我們取參數N=5000,m=4,p=0.5的小世界網來驗證平均場近似的合理性，另外，取定參數ε=0.3,r=0.5,δ=0.4，取20個網絡現實，每個現實做40次傳播，然后取平均，當ρ2=0.05時，E,I,Q分別隨ρ2變化的曲線的模擬結果見圖2，當ρ1=0.02時，E,I,Q分別隨ρ2變化的曲線的模擬結果見圖4，由圖可知，當ρ2=0.05，ρ1=0.03時，閾值H=1，與理論值符合得較好。

所以，本文借鑒SEIQ類傳染模型[11,12]，對隱性知識網絡傳播行為進行了仿真過程的演示，基于平均場理論和數值的基礎，對均勻網絡上的傳播臨界的特性進行了模擬研究。研究結果表明：對于隱性知識均勻網絡，存在隱性知識傳播臨界閾值且該閾值與隱性知識隔離率、隱性知識潛伏期的隱性知識傳播等有關，隱性知識傳播行為具有網絡性。

[1]Newman M E J.Spread of Epidemic Disease on Networks[J].Physical Review E，2002，66(1).

[2]許丹，汪小帆.局域世界復雜網絡中的病毒傳播及其免疫控制[J].控制與決策，2006，21(7).

[3]Xia C Y，Liu Z X，Chen Z Q，et al.Dynamic Spreading Behavior of Homogeneous and Heterogeneous Networks[J].Progress in Natural Science，2007，17(3).

[4]李光正，史定華.復雜網絡上SIRS類疾病傳播行為分析[J].自然科學進展，2006，（3）.

[5]夏承遺，劉忠信，陳增強，袁著祉.復雜網絡上帶有直接免疫的SIRS 類傳染模型研究[J].控制與決策，2008，23（4）.

[6]陳蘭蓀，陳鍵.非線性生物動力系統[M].北京:科學出版社，1993.

[7]叢海濤，唐元虎.隱性知識轉移、共享的激勵機制研究[J].科研管理，2007，(1).

[8]劉志國,崔健.醫院科技創新與隱性知識共享[J].中國醫院管理,2006，(5).

[9]張方華.知識型企業的社會資本與知識獲取關系研究[J].科學學研究,2006,24(1).

[10]王夏潔,劉紅麗.基于社會網絡理論的知識鏈分析[J].情報雜志,2007,(2).

[11]林向義.知識不對稱網絡中隱性知識共享的分析與優化[J].情報科學，2008,（2）.

[12]楚揚杰;周佳華.SEIQ類疾病在小世界網絡上的傳播行為分析[J].計算機工程與應用，2009，（3）.

(責任編輯/亦 民)

R197.3

A

1002－6487（2011）03－0082-03

曹 征（1978-），男，湖南郴州人，博士研究生，中級經濟師，研究方向：知識共享研究。