用MRCI方法研究CS+同位素離子X2Σ+和A2Π態的光譜常數與分子常數*

劉 慧 邢 偉 施德恒? 朱遵略 孫金鋒

1)(信陽師范學院物理電子工程學院，信陽 464000)

2)(河南師范大學物理與信息工程學院，新鄉 453007)

1.引 言

在星際分子云中，已觀測到許多含硫化合物，如 CS，CS+，HCS，HCS+，C2S及 C5S 等［1—4］. 其中CS+在電荷轉移反應形成星際介質CS的過程中起重要作用［5］，其光譜特性已引起人們的廣泛關注.在過去的幾十年里，人們已對這一離子的各種光譜性質進行了大量的研究［5—25］.

實驗方面，Jonathan 等［6］，King 等［7］和 Frost等［8］于1972年報告了該離子的真空遠紫外光電子譜，進行了振動分析并得到了少量的光譜常數.1975年，List等［9］在觀測 CS的光譜時指出，CS+離子在星際空間肯定存在.1976年，Coxon等［10］在研究He(23S)與 CS2的碰撞中觀測到了 CS+離子的A2Π→X2Σ+躍遷，并獲得了該離子 X2Σ+和 A2Π 態的某些光譜常數和若干低振動態的振動能級、經典轉折點等分子常數.1977年，Gauyacu等［5］在600—800 nm內記錄了CS+離子的發射譜并分析了A2Π→X2Σ+轉動躍遷，得到了該離子 X2Σ+和 A2Π態的部分光譜常數和某些分子常數.1980年Tsuji等［12，13］在 220—340 nm 內觀測并標識了該離子的B2Σ+→X2Σ+譜帶、對其進行了振動分析并擬合出了部分光譜常數.1981年 Obase等［15］由 CS+的B2Σ+-A2Π 及 B2Σ+-X2Σ+譜線導出了 B2Σ+態 υ′=0—6 的振動分布.1993年 Cossart等［17］根據CS+離子 B2Σ+—X2Σ+和 B2Σ+- A2Π 的發射譜，擬合得到了少量的分子常數.1995年Coppens等［18］從對CS的光游離質譜分析中，得到了 CS+離子基態的離解能.2000—2002 年間，Liu等［20，21］利用激光吸收譜對 CS+離子的 A2Π←X2Σ+躍遷進行了詳盡的研究，并擬合出了該離子 X2Σ+和 A2Π電子態的若干振動態的轉動慣量、離心畸變常數及振動能級.綜合已有的實驗數據可以看出，僅有的實驗研究都只涉及該CS+離子的部分光譜常數和較低振動態的分子常數;對于較高振動態的分子常數及12C34S+和12C33S+等同位素離子，實驗暫未涉及.

理論方面，僅有 Larsson［22］，Midda 等［23］和Honjou［24，25］先后開展過類似的研究工作.1985 年Larsson［22］采用完全活性空間自洽場(CASSCF)及組態相互作用方法計算了該離子X2Σ+，A2Π和B2Σ+態的勢能曲線并擬合出了各態的光譜常數;2003年，Midda等［23］采用密度泛函(HF/DF B3LYP)方法對該離子基態的鍵長、諧振頻率等光譜常數等進行了探討;2006年，Honjou［24］利用組態相互作用方法計算了 CS+前5個2Σ+態及前3個2Π 態的電子結構和能量，得到了相應的光譜常數.2008年Honjou［25］再 次 對該離子 的 X2Σ+，A2Π，B2Σ+及C2Σ+態進行研究，擬合出了各態的光譜常數及某些振動能級.顯見，已有的理論計算［22—25］對 X2Σ+和A2Π態的Re與ωe研究較多，但其它光譜常數卻涉及較少，且這些計算結果均偏離實驗值較大，同時所有的理論計算都未涉及同位素識別.雖然也有理論［25］計算振動能級，但得到的結果卻偏離實驗值較大.鑒于這些原因，本文對該離子 X2Σ+和A2Π態的光譜常數及振動能級等分子常數進行了詳盡的研究.

12C和13C的天然豐度大約是98.93% 和1.07%.14C是放射性元素，含量極低.S有4個穩定同位素32S，33S，34S和36S，天然豐度分別為95.02%，0.75%，4.21%和0.02%.本文僅研究豐度相對較大的3個同位素離子:12C32S+(豐度94.00%)、12C34S+(豐度4.16%)和12C33S+(豐度0.74%).

本文使用內收縮多參考組態相互作用(MRCI)方法［26，27］和價態范圍內的最大相關一致基 aug-ccpV6Z［29—31］在 Molpro 程 序 包［28］中 計 算 CS+離 子X2Σ+和A2Π態的勢能曲線.利用這些勢能曲線并通過同位素質量識別，擬合出12C32S+，12C34S+和12C33S+等同位素離子的光譜常數.最后通過求解雙原子分子徑向核運動的Schr?dinger方程，找到CS+(X2Σ+)及CS+(A2Π)離子的全部振動態.針對每一振動態，在同位素識別的基礎上還計算了它們的經典轉折點、轉動慣量及離心畸變常數.這些計算結果均與已有的實驗數據相符很好.

2.計算方法

MRCI方法是一種可靠的勢能曲線計算方法［32，33］.在勢能曲線的計算中 MRCI方法只使用Abelian點群.CS+離子屬于線性雙原子分子離子，具有C∞υ對稱性，因此在計算中只能由其子群 C2υ替代.C2υ子群共有4種類型的分子軌道，相對應的不可約表示是a1/b1/b2/a2.具體到含有21個電子的CS+離子，分析指出它默認參與運算的分子軌道有14個，分別是8個 a1，3個 b1和3個 b2軌道.其中，8個屬于開殼層軌道(4a1，2b1和2b2)，分別對應于C原子的2s2p和S原子的3s3p軌道;6個屬于閉殼層軌道，分別是4a1，1b1和1b2.

我們發現，當只采用這14個分子軌道(8a1，3b1，3b2)進行計算時，所得這兩個態的勢能曲線都不光滑.原因是一個態的勢能曲線與另一個態有交叉.以A2Π態為例，當核間距約0.40 nm時，勢能曲線出現跳變(由一個態跳到另一個態).這提示我們，為得到光滑的勢能曲線，需要將更多的軌道放入活化空間.計算發現，當將1個額外的a1軌道、1個額外的b2軌道放入活化空間時(此時參與計算的分子軌道共16個，分別是9a1，3b1和4b2)，所得這兩個態的勢能曲線是光滑的.

MRCI計算以 CASSCF 波函數［34，35］為參考波函數.為得到滿意的結果，這里C和S均使用價態范圍內的最大相關一致基.即 C原子是(16s，10p，5d，4f，3g，2h，1i)/［7s，6p，5d，4f，3g，2h，1i］，S 原子是(21s，14p，5d，4f，3g，2h，1i)/［8s，7p，5d，4f，3g，2h，1i］，均記為 aug-cc-pV6Z.

為準確計算該離子X2Σ+和A2Π態的離解能，本文首先在MRCI/aug-cc-pV6Z理論水平下對其進行幾何優化，以便在進行勢能曲線計算時，平衡位置能準確地成為勢能曲線的一個計算點.當核間距達到0.60 nm左右時，這兩個態的勢能值都保持為一個常數而不隨核間距的增大而發生變化，因此勢能曲線的計算范圍可取為0.05—0.60 nm.計算過程中，步長一般取0.05 nm，只是在平衡位置附近為清晰展現這兩個態的細節特性，計算步長才取為0.02 nm.掃描得到的這兩個態的勢能曲線都是完全收斂的.

計算中，我們也在一個較小的核間距范圍內考慮了相對論效應及核價相關效應對光譜常數計算結果的影響.我們發現，這兩種修正對光譜常數的影響都很小.考慮到在一個較大的核間距范圍內進行這兩種修正需要耗費大量機時，而且價態范圍內的計算結果已經能很好地反映該離子的光譜特性，因此本文所述的計算僅在價態范圍內進行.

利用Molcas程序包［36］擬合上述勢能曲線并進行同位素識別，即可得到CS+各種同位素離子的光譜常數和分子常數.其中12C32S+，12C34S+和12C33S+的光譜常數列于表1中，12C32S+的分子常數則分別列于表2—5中.由于篇幅限制，表2—5只列出了前30個振動態的振動能級G(υ)、轉動慣量Bυ及離心畸變常數Dυ.需要說明地是，由于12C32S+在CS+的各種同位素離子中所占的份額高達94%，因此對于那些未進行同位素識別的理論或實驗結果，本文中都將其歸類于12C32S+.

另外，本文還將這兩個電子態的前30個振動態的經典轉折點列于表2和表4中，以便于分析和比較.

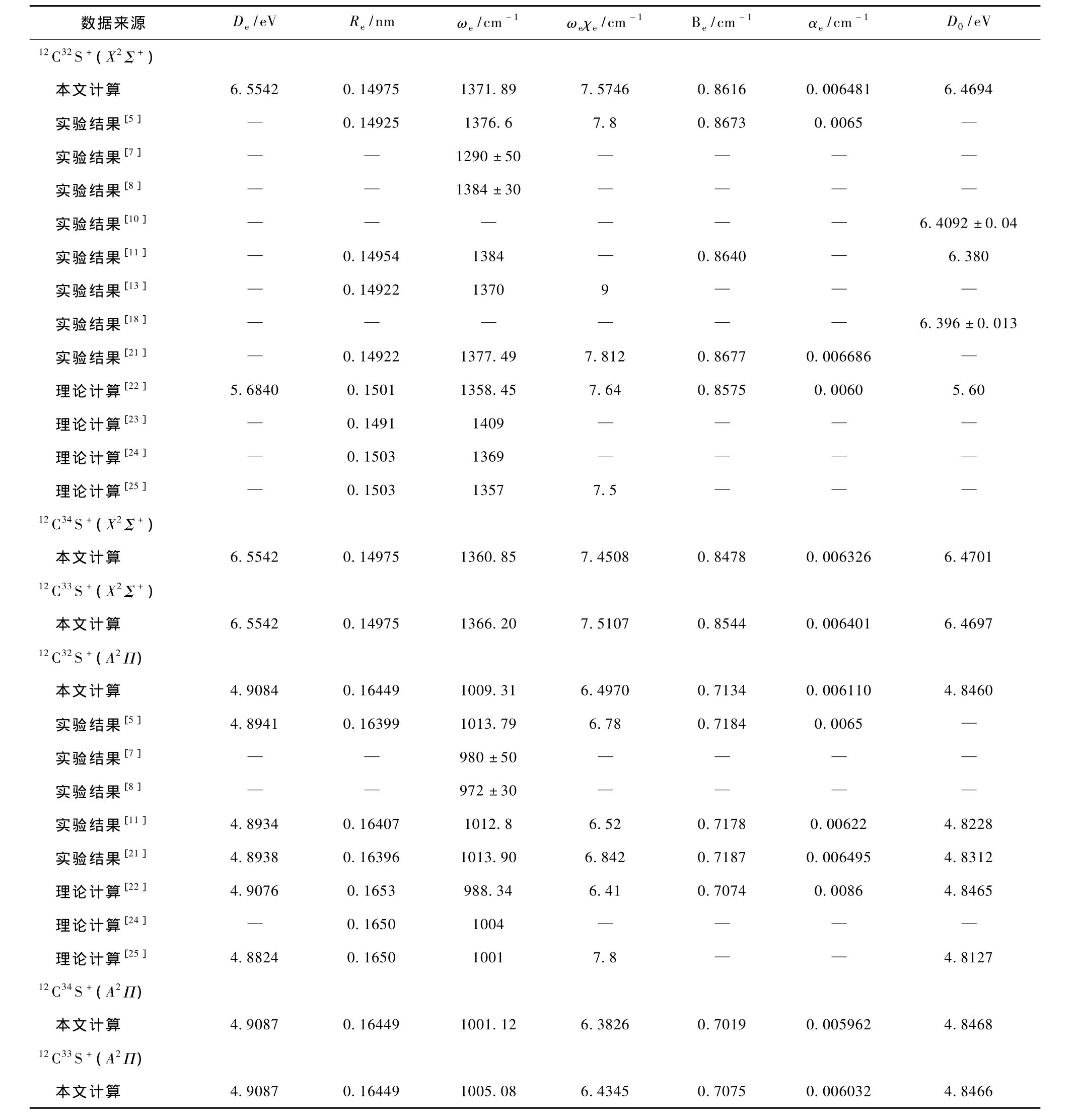
表1 MRCI/aug-cc-pV6Z理論水平下CS+各種同位素離子X2Σ+和A2Π態的光譜常數及與實驗結果和其他理論結果的比較

3.結果與討論

3.1.光譜常數

為便于比較，表1還列出了已有的實驗結果［5，7，8，10，11，13，18，21］及其他理論結果［22—25］. 在這些計算結果中，較早的工作是由 Larsson［22］于1985年報道的.Larsson［22］采用CASSCF和組態相互作用方法在一個較小的核間距范圍內計算了該離子X2Σ+，A2Π 和 B2Σ+態的勢能曲線.計算中，C原子使用［14s，l0p，4d］/(8s，6p，4d)高斯收縮基;S原子使用［10s，6p］/(5s，4p)Dunning-Huzinaga基.利用得到的勢能曲線，Larsson［22］擬合出了這些態的部分光譜常數.與實驗結果［18］比較后發現，對于X1Σ+態，Larsson［22］的 D0值偏離該實驗值［18］竟高達12.45%.諧振頻率偏離實驗結果［21］雖較小，但也有1.38%.對 A2Π 態來說，其 ωe比實驗值［21］低了近26 cm-1，誤差達2.52%.由于該態的離解能僅是在計算一小段勢能曲線的基礎上擬合得到的，因此其可靠性并不高.

2003年，Midda等［23］采用密度泛函(HF/DF B3LYP)方法和四個基組(從 6-311++G(2df，2pd)，6-311++G(3df，3pd)，cc-pVTZ，aug-ccpVTZ)對若干雙原子分子及其離子的光譜性質進行了研究.關于CS+，他們計算了其基態的平衡核間距和諧振頻率.與實驗結果［21］比較后發現，當使用最大基組aug-cc-pVTZ時，他們得到的平衡核間距與這一實驗值僅相差0.0001 nm.不過我們發現，雖然 Midda等［23］的 Re很準確，但其 ωe卻比實驗值［21］高2.3%.更重要地，他們沒有計算該離子的其他光譜常數(如 De，ωeχe，αe和 Be等)，因而其結果存在很大的局限性.

2006 年，Honjou［24］用 MRCI方法在一個較小的核間距范圍內計算了該離子前5個2Σ+態及前3個2Π態的勢能曲線.通過擬合，他們得到了相應于各態的光譜常數(Te，Re和ωe).計算中，C和S均使用高斯型基函數.與實驗結果［21］比較后發現，Honjou［24］得到的 Re和 ωe較為準確. 例如對于X1Σ+態，其 Re值只偏離這一實驗結果［21］0.72%;ωe偏離這一實驗結果［21］也只有0.62%;對 A2Π 態來說，Re值偏離這一實驗結果［21］只有0.63%;ωe偏離這一實驗結果［21］也只有0.98%，等等.但遺憾地是，Honjou［24］沒有對該離子的其它重要光譜常數(如 De，ωeχe等)進行研究.最近，Honjou［25］用SOCI方法在一個較小的核間距范圍內再次對該離子 X2Σ+，A2Π，B2Σ+及 C2Σ+態的勢能曲線進行了計算，也獲得了各態的光譜常數 Te，Re，ωe及ωeχe..通過比較我們發現，對于 X1Σ+和 A2Π 態，其Re值沒有變化;但其 ωe偏離實驗結果［21］的卻明顯加劇，因而對于光譜常數來說，文獻［25］的計算質量未得到改善.

對于12C32S+(X2Σ+)，一方面，本文得到的平衡核間距Re及諧振頻率 ωe與實驗值［21］間的偏差只有 0.00053 nm和 5.6 cm-1，相對誤差僅為0.36%和0.41%，顯然優于文獻［22，24，25］的計算結果.雖然文獻［23］得到的 Re與實驗結果［21］的偏差小于本文，但其 ωe值卻偏離實驗值［21］較大，且沒有計算其他光譜常數;另一方面，本文的Be與實驗值［21］間的相對誤差也只有0.70%，顯然優于文獻［22］的計算結果.盡管本文的 αe與實驗值［21］相比低了0.000205 cm-1，但與僅有的理論值［22］相比，本文結果有明顯改善.至于D0值，本文的結果與實驗值［10］間的偏差為0.94%，也大大優于文獻［22］的計算結果.

對于12C32S+(A2Π)，一方面本文得到的 Re及ωe偏離實驗值［21］分別只有0.32%和0.45%，這優于文獻［22，24，25］的計算結果;另一方面，本文的 Be，αe及 ωeχe也與實驗結果［21］符合很好，優于文獻［22］得到的理論值.

據此以上分析可以得出結論:對于12C32S+(X1Σ+)及12C32S+(A2Π)，本文的光譜計算結果與實驗值相當一致，并在總體上明顯優于已有的理論值.這些都說明本文所采用的計算方法是可靠的，得到的光譜常數是準確、可信的.

遺憾地是，由于暫時還沒有同位素離子12C34S+和12C33S+的實驗或理論光譜常數，這里無法進行直接的數據比較.但前文的討論和后文的分析結果都告訴我們，本文得到的勢能曲線是準確、可靠的.由于本文使用的擬合方法［37—40］十分可靠，因此我們有理由相信表1列出的同位素離子12C34S+和12C33S+在這兩個態的光譜常數也是可信的.

3.2.分子常數

利用本文得到的勢能曲線，通過求解核運動的徑向薛定諤方程，找到了 J=0時 CS+(X2Σ+)的全部68個振動態及 CS+(A2Π)的全部80個振動態.在 Molcas程序包［36］中，通過同位素質量識別還計算了每一振動態的振動能級、轉動慣量及離心畸變常數等，并將計算結果分別列入表2—5中.為便于比較，表2—5也列出了已有的實驗結果［5，16，17，20，21］及其他理論計算結果［25］.

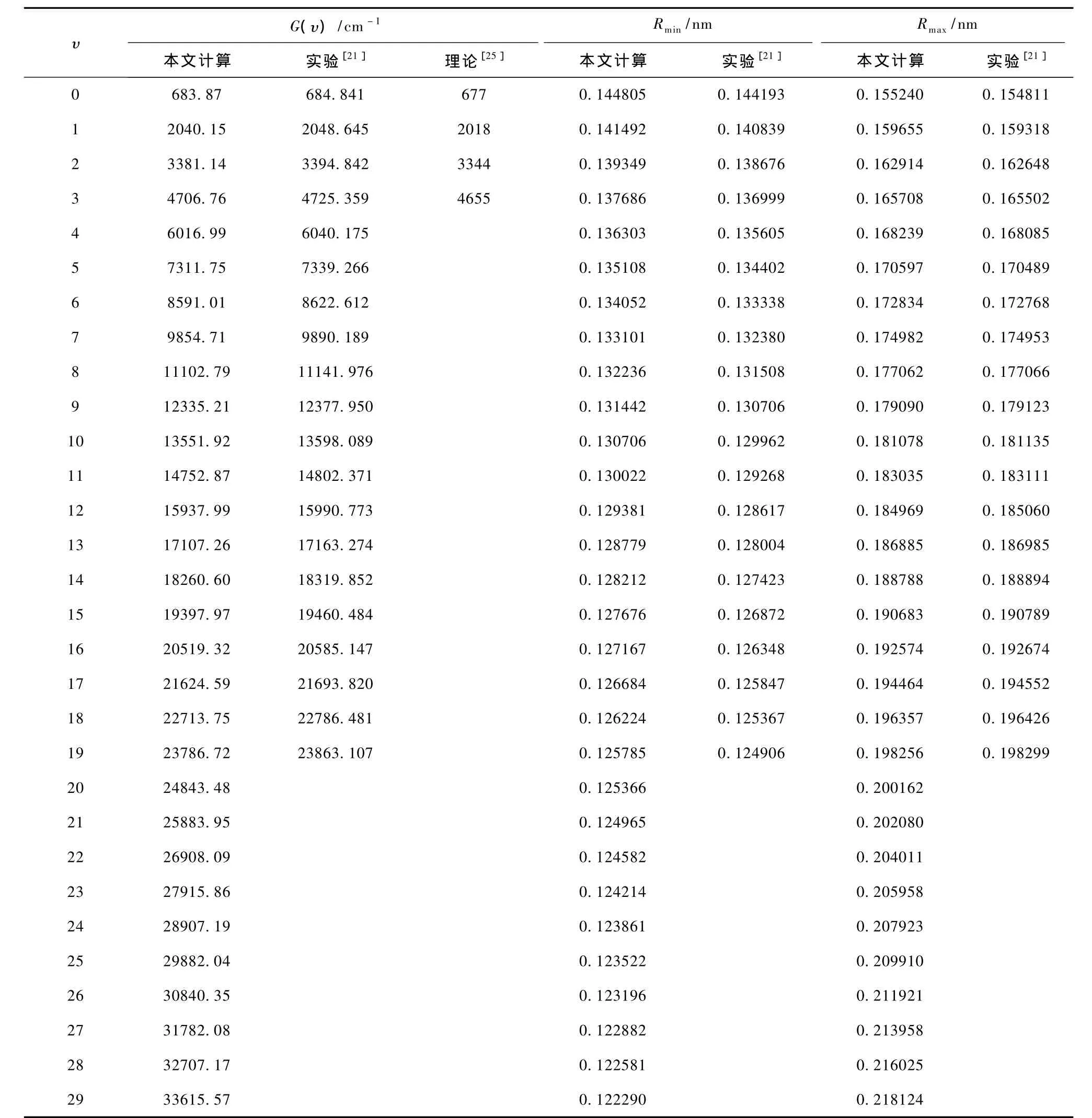
表2 MRCI/aug-cc-pV6Z理論水平下12C32S+(X2Σ+)的振動能級和經典轉折點(J=0時)及與實驗結果和其他理論結果的比較

只有一組實驗［21］報道了該離子 X2Σ+態的振動能級與經典轉折點(Rmin和 Rmax)，也只有一組理論［25］涉及該態振動能級的計算.一方面，從表2不難發現，本文得到的振動能級與實驗值［21］的最大偏離不超過 0.40%，而 Honjou［25］的理論值與實驗值［21］的最小偏離也有1.15%，因此本文的振動能級比僅有的理論計算結果［25］更加接近實驗值［21］;另一方面，經典轉折點也與僅有的一組實驗結果［21］相當一致(Rmin和Rmax與該組實驗數據的最大偏離也分別只有0.70%和0.28%)，都是十分準確的.

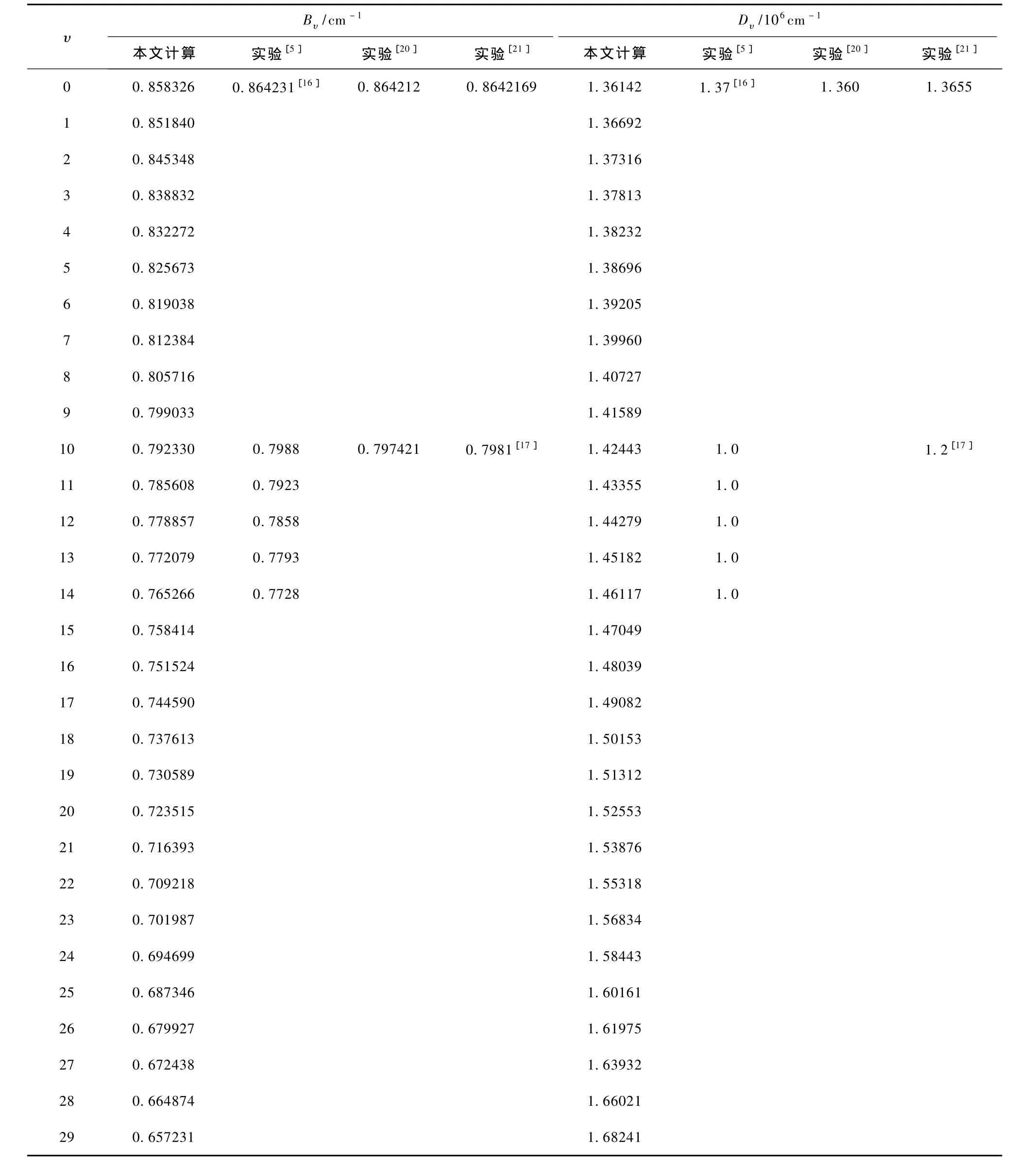
表3 MRCI/aug-cc-pV6Z理論水平下12C32S+(X2Σ+)的轉動慣量和離心畸變常數(J=0)及與實驗結果的比較

表3列出了本文得到的12C32S+(X2Σ+)離子的轉動慣量 Bυ、離心畸變常數 Dυ及相應的實驗結果［5，16，17，20，21］. 與這些實驗結果相比，Bυ的最大偏差 分 別 只 有 0.97%［5］，0.68%［16］，0.72%［17］，0.68%［20］和 0.68%［21］，是非常準確的. 這里需要說明的是，實驗［5］給出的Bυ值是在固定 Dυ值的基礎上擬合得到的.因此實驗［5］中的 Dυ值不具有可比性.

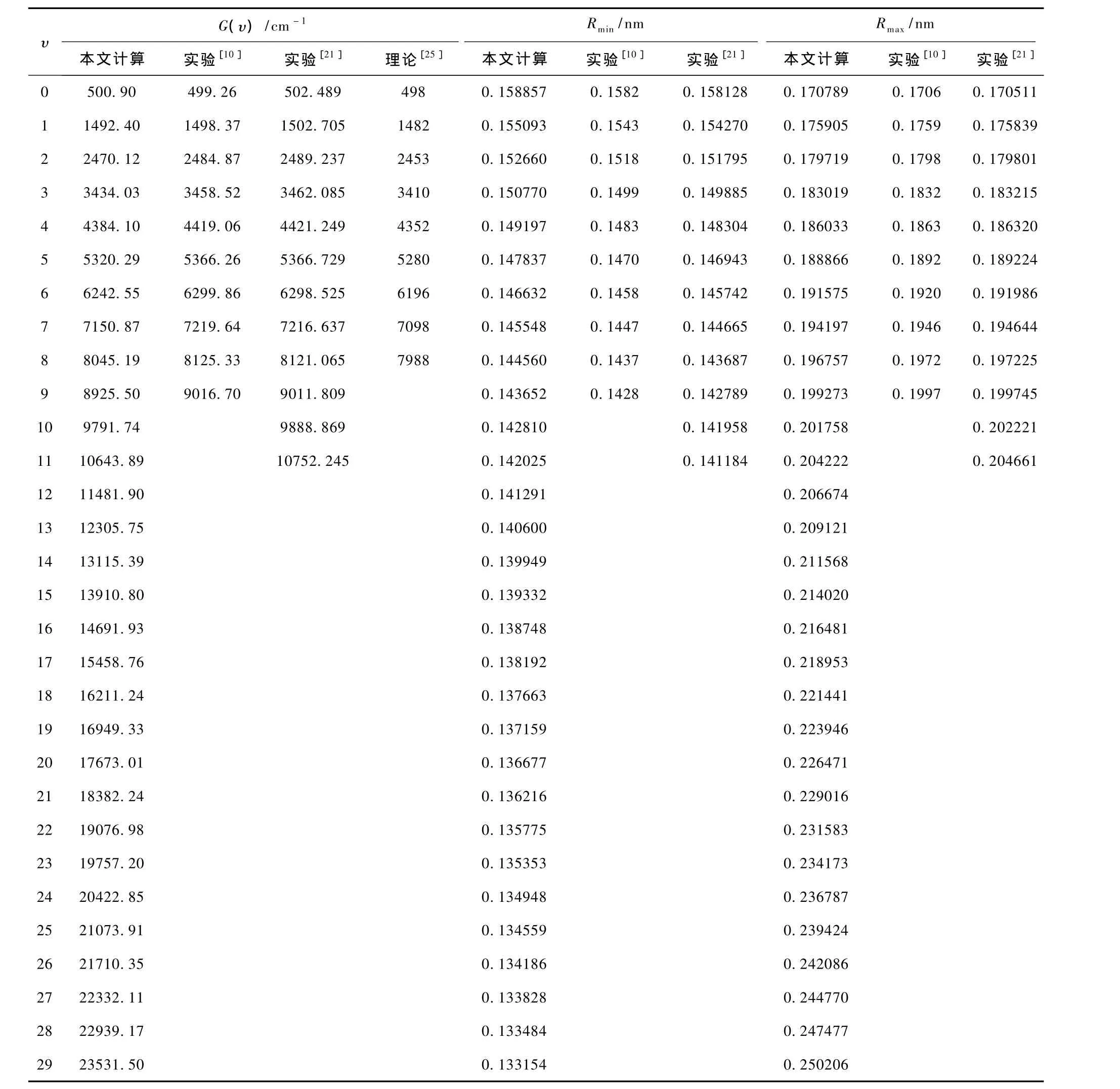
表4 MRCI/aug-cc-pV6Z理論水平下12C32S+(A2Π)的振動能級和經典轉折點(J=0)及與實驗結果和其它理論結果的比較

關于12C32S+(A2Π)，表4列出了本文得到的振動能級G(υ)、經典轉折點(Rmin和Rmax)及已有的實驗結 果［10，21］和 理 論 計 算 結 果［25］. 一 方 面， 與Honjou［25］的計算結果相比，除個別數據點外，本文的振動能級均更加接近實驗值［10，21］.例如當υ=0時，雖然與實驗［10］相比本文結果與理論結果［25］有相當的精度，但與文獻［21］的實驗相比本文的計算結果只略低0.32%，而文獻［25］則偏低0.9%.當υ=8時與文獻［21］的實驗相比較，本文結果只偏離0.93%，而文獻［25］則達到 1.64%;與文獻［10］的實驗相比較，本文結果偏離0.99%，而文獻［25］則達到1.69%.另一方面，本文計算所得的經典轉折點也與實驗值［10，21］相當一致.詳細的分析結果還表明，本文的Rmin和Rmax偏離實驗結果［21］的最大值分別只有0.61%和0.24%，這些都是相當令人滿意的.

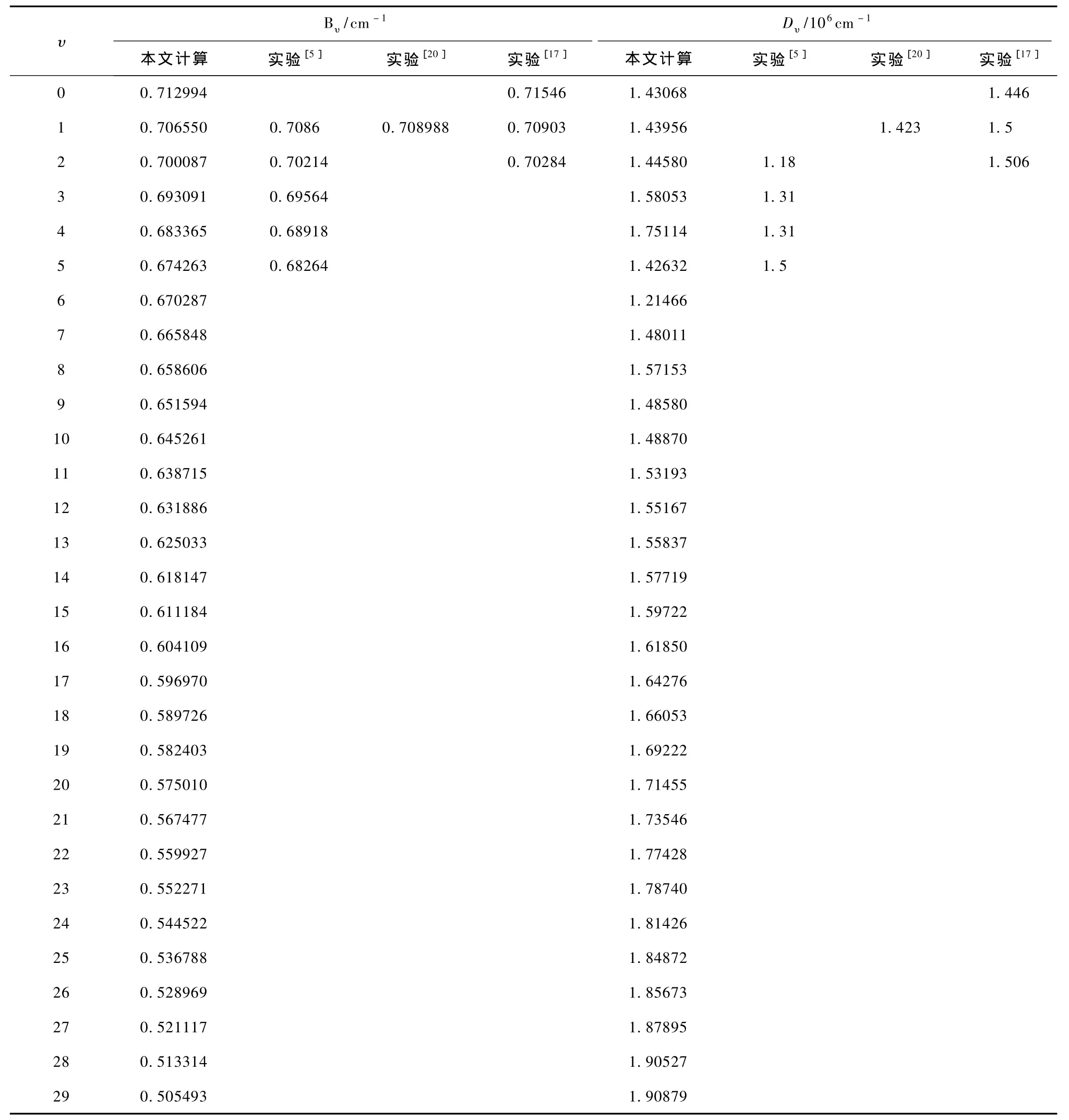
表5 MRCI/aug-cc-pV6Z理論水平下12C32S+(A2Π)的轉動慣量及離心畸變常數(J=0)及與實驗結果的比較

表5列出了12C32S+離子A2Π態的轉動慣量、離心畸變常數及其相關實驗結果［5，17，20］. 先分析 Bυ偏離實驗結果的情況.與實驗結果［17］相比，本文結果與其偏差最大不到0.40%，是非常好的;與實驗結果［5］相比，本文值與其偏差最大也只有1.23%(這對應于υ=5的情況.除該點外，其余各點的最大偏差都不超過0.85%).另外，本文的計算結果與實驗報道的僅有的實驗值［20］也僅偏差0.34%.據此可以得出結論:本文得到的A2Π態的轉動慣量是準確、可靠的.至于高階小量Dυ，從表5也不難看出，本文的計算結果與實驗值也很符合.

對于較高的振動態，文獻中沒有相關的實驗數據及理論計算結果報道.但根據前面關于較低振動態的計算結果與實驗結果及其他理論計算結果的比較與分析，我們足以相信，本文關于較高振動態的分子常數計算結果是準確、可靠的.本文關于較高振動態的計算結果可為進一步的實驗研究提供可靠的數據參考.

4.結 論

本文利用精度較高的MRCI方法和價態范圍內的最大相關一致基aug-cc-pV6Z，在0.05—0.60 nm的核間距范圍內計算了 CS+(X2Σ+)和 CS+(A2Π)的勢能曲線.利用得到的勢能曲線并通過同位素質量標識，擬合得到了這兩個態3種主要同位素分子離子的光譜常數 D0，De，Re，ωe，ωeχe，αe和 Be.本文的計算結果與已有的實驗值均符合很好.利用本文得到的勢能曲線，通過求解核運動的徑向薛定諤方程，找到了 J=0時 CS+(X2Σ+)和 CS+(A2Π)的全部振動態，在同位素質量識別的基礎上分別計算了每一振動態的振動能級、經典轉折點、轉動慣量及離心畸變常數等分子常數，所得結果也與實驗數據一致.本文中，CS+離子兩個電子態的同位素光譜常數和高振動態的分子常數系首次報道.

［1］Penzias A A，Solomon P M，Wilson R W，Jefferts K H 1971 Astrophys.J.，Lett.Ed.168 L53

［2］Thaddeus P，Guelin M，Linke R A 1981 Astrophys.J.Lett.，Ed.246 L41

［3］Saito S，Kawaguchi K，Yamamoto S，Ohishi M，Suzuki H，Kaifu N 1987 Astrophys.J.，Lett.Ed.317 L115

［4］Bell M B，Avery L W，Feldman P A 1993 Astrophys.J.Lett.417 L37

［5］Gauyacq D，Horani M 1978 Can.J.Phys.56 587

［6］Jonathan N，Morris A，Okuda M，Smith D J，Ross K J 1972 Chem.Phys.Lett.13 334

［7］King G H，Kroto H W，Suffolk R J 1972 Chem.Phys.Lett.13 457

［8］Frost D C，Lee S T，McDowell C A 1972 Chem.Phys.Lett.17 153

［9］List H S，Linke R A 1975 Astrophys.J.196 709

［10］Coxon J A，Marcoux P J，Setser D W 1976 Chem.Phys.17 403

［11］Huber K P，Herzberg G 1979 Molecular Spectra and Molecular Structure.(Vol.4)Constants of Diatomic Molecules(New York:Van Nostrand Reinhold Company)p184

［12］Tsuji M，Obase H，Nishimura Y 1980 J.Chem.Phys.73 2575

［13］Tsuji M，Obase H，Matsuo M，Endoh M，Nishimura Y 1980 Chem.Phys.50 195

［14］Erman P，Larsson M 1981 Physica Scripta 23 1052

［15］Obase H，Tsuji M，Nishimura Y 1981 Chem.Phys.57 89

［16］Horani M，Vervloet M 1992 Astron.Astrophys.256 683

［17］Cossart D，Horani M，Vervloet M 1993 Am.Inst.Phys.Conf.Proc.312 367

［18］Coppens P，Drowart J 1995 Chem.Phys.Lett.243 108

［19］Turner B E 1996 Astrophys.J.468 694

［20］Liu Y，Liu H，Gao H，Duan C，Hamilton P A，Davies P B 2000 Chem.Phys.Lett.317 181

［21］Liu Y，Duan C，Liu J，Wu L，Xu C，Chen Y，Hamilton P A，Davies P B 2002 J.Chem.Phys.116 9768

［22］Larsson M 1985 Chem.Phys.Lett.117 331

［23］Midda S，Das A K 2003 Eur.Phys.J.D 27 109

［24］Honjou N 2006 Chem.Phys.324 413

［25］Honjou N 2008 Chem.Phys.344 128

［26］Werner H J，Knowles P J 1988 J.Chem.Phys.89 5803

［27］Knowles P J，Werner H J 1988 Chem.Phys.Lett.145 514

［28］Werner H J，Knowles P J，Lindh R，Manby F R，Schütz M，Celani P，Korona T，Mitrushenkov A，Rauhut G，Adler T B，Amos R D，Bernhardsson A，Berning A，Cooper D L，Deegan M J O，Dobbyn A J，Eckert F，Goll E，Hampel C，Hetzer G，Hrenar T，Knizia G，K?ppl C，Liu Y，Lloyd A W，Mata R A，May A J，McNicholas S J，Meyer W，Mura M E，Nicklass A，Palmieri P，Pflüger K，Pitzer R，Reiher M，Schumann U，Stoll H，Stone A J，Tarroni R，Thorsteinsson T，Wang M，Wolf A 2008 Molpro，version 2008.1，a package of ab initio programs

［29］Peterson K A，Kendall R A，Dunning T H 1993 J.Chem.Phys.99 1930

［30］Woon D E，Dunning T H 1993 J.Chem.Phys.99 1914

［31］Dunning T H 1989 J.Chem.Phys.90 1007

［32］Wang X Q，Yang C L，Su T，Wang M S 2009 Acta Phys.Sin.58 6873(in Chinese)［王新強、楊傳路、蘇 濤、王美山 2009物理學報58 6837］

［33］Bai F J，Yang C L，Qian Q，Zhang L 2009 Chin.Phys.B 18 549

［34］Werner H J，Knowles P J 1985 J.Chem.Phys.82 5053

［35］Knowles P J，Werner H J 1985 Chem.Phys.Lett.115 259

［36］Krogh J W，Lindh R，Malmqvist P°A，Roos B O，Veryazov V，Widmark P O 2009 User Manual，Molcas Version 7.4(Lund:Lund University)

［37］Shi D H，Zhang X N，Sun J F，Zhu Z L 2010 Chin.Phys.B 19 013501

［38］Shi D H，Zhang J P，Sun J F，Liu Y F，Zhu Z L 2009 Acta Phys.Sin.58 5329(in Chinese)［施德恒、張金平、孫金峰、劉玉芳、朱遵略 2009物理學報 58 5329］

［39］Zhang X N，Shi D H，Zhang J P，Zhu Z L，Sun J F 2010 Chin.Phys.B 19 053401

［40］Shi D H，Zhang J P，Sun J F，Liu Y F，Zhu Z L 2009 Acta Phys.Sin.58 7646(in Chinese)［施德恒、張金平、孫金峰、劉玉芳、朱遵略 2009物理學報 58 7646］