關于組合范疇語法CCG

鄒崇理

(1.燕山大學文法學院，河北秦皇島 066004;2.中國社會科學院哲學研究所，北京 100732)

關于組合范疇語法CCG

鄒崇理1，2

(1.燕山大學文法學院，河北秦皇島 066004;2.中國社會科學院哲學研究所，北京 100732)

組合范疇語法CCG(Combinatory Categorial Grammar)和類型邏輯語法TLG(Type Logical Grammar)都是范疇語法的現代版本，前者關注范疇語法的語言學應用和自然語言的信息處理，后者傾向于從邏輯的角度審視范疇語法的理論性質。CCG的特點有:原子范疇的加標多樣化和徹底的詞匯主義思路;斜線算子的下標模態化和函子范疇的多樣組合;基于范疇等級和范疇構造的視角建立CCG的證明論。

組合范疇語法CCG;類型邏輯語法TLG;函子范疇的組合

范疇語法是一種面向自然語言信息處理的邏輯理論。按照這種理論，自然語言是由詞構成詞組、詞組構成語句的符號系統，自然語言的這種構造生成被看作是計算推演的過程。范疇語法產生于20世紀30～40年代，50年代以后逐步走向成熟。

組合范疇語法 CCG(Combinatory Categorial Grammar，簡稱CCG)則在20世紀80～90年代開始出現，是對范疇語法進行擴展的現代版本。擴展的實質在于“組合”(combinatory)，即基于范疇語法增添了函子范疇的組合運算，這類似數學中函數的復合。與此同時，類型邏輯語法TLG(Type Logical Grammar，簡稱TLG)也是范疇語法發展的現代產物，這個發展方向的源頭是著名的蘭貝克演算(Lambek，1958)。自誕生起CCG和TLG就顯示出各自側重的偏好。CCG關注自然語言“語境敏感層面”的表達力問題，從語言學和計算語言學的角度探討基于統計模型的自然語言的自動機處理問題。而TLG的蘭貝克傳統則熱心于范疇語法的邏輯理論問題，把范疇語法看成是一個邏輯系統，配備框架語義學，討論系統的可靠性和完全性，以及系統的可判定性。本文從范疇語法的基礎出發，進而介紹CCG，看看這個理論到底具有哪些不同于TLG的內容。

跟范疇語法一脈相承，CCG也是一種基于詞匯的語法形式理論。就是說，CCG把自然語言的生成過程凝縮在詞條的范疇構造上［1］。例如:

我們可以通過詞條“proved”的范疇構造(2)來體現生成規則(1)的內容。從某種意義上說，(1)確定了(2)。根據(1)，我們有生成樹:

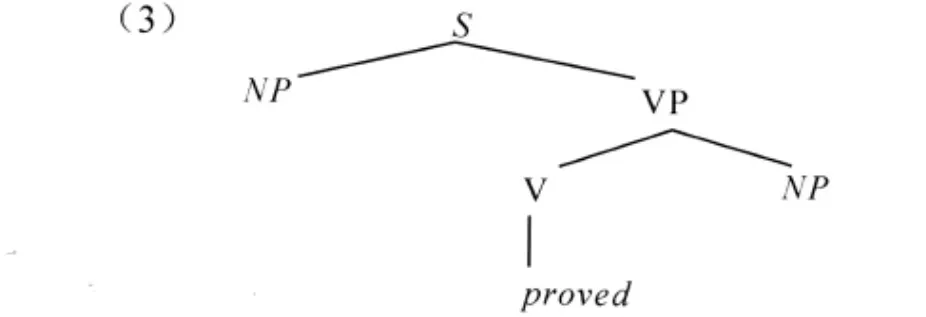
按照(3)從上到下看，節點VP對應的函子范疇是:運算的論元是NP，運算的結果是S，記作S NP，其運算是向后的，即論元范疇在函子范疇的后邊。而節點V對應的函子范疇為:論元是NP，結果是SNP，記作(SNP)/NP，其運算是向前的，即論元在函子的前邊。(SNP)/NP就是詞條Proved對應的范疇。因此說，范疇語法指派給動詞的函子范疇的構造顯示出:運算前的論元范疇和運算后的結果范疇以及運算的方向。于是，CCG從范疇語法那里傳承的函項應用于論元的規則為［1］:

向前的應用

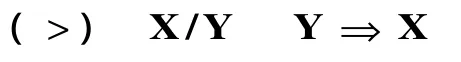
向后的應用

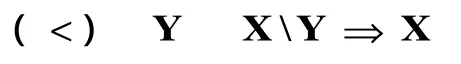
以上規則就是CCG對范疇語法基本思想的繼承。除此以外，CCG還發展出自己新的內容，概括為三點:原子范疇的加標多樣化和徹底的詞匯主義思路;斜線算子的下標模態化和函子范疇的多樣組合規則;基于范疇等級和范疇構造的概念建立CCG的證明論。

首先，CCG為刻畫豐富多彩的自然語言，其范疇設置比TLG更加精細化。對原子范疇譬如N， NP，PP，S等等，可以通過添加數格等標記進一步多樣化，如名詞短語范疇根據數的特征分為NPsg和NPpl，根據格的特征分為NPsbj和NPobj，還有主格復數名詞短語范疇NPplsbj等等。CCG是徹底的詞匯主義語法理論，詞庫中甚至還有詞綴的范疇指派［2］:

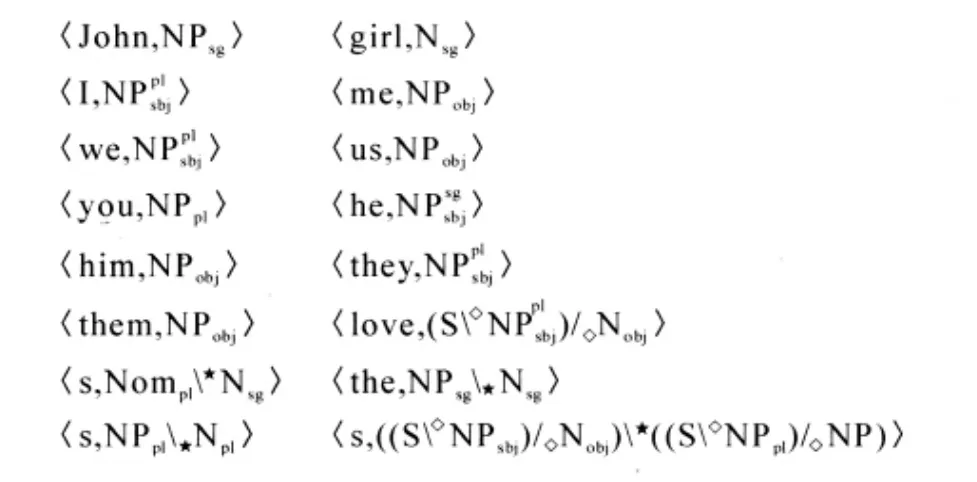
圖1 詞庫

圖1這樣的詞庫顯示:第一列的第七行就是對名詞的復數詞綴的范疇指派，第二列第八行就是對第三人稱動詞詞綴的范疇指派。基于這樣的詞庫，CCG關于動詞第三人稱詞綴和名詞復數詞綴的推演例子如圖2［2］:

圖2 推演例

其次，純粹的范疇語法限于函項應用于論元的句法貼合規則，這樣限制了語境自由文法的表達力。CCG擴大了語境自由文法的規則集合，添加了基于函子范疇的組合(置換)獲得另一函子范疇的那些規則。如:

函子范疇的向前組合

函子范疇的向后組合

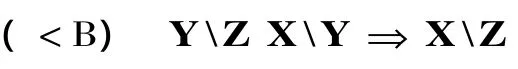
函子范疇的向前置換

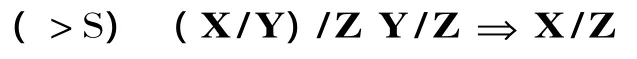
函子范疇的向后置換

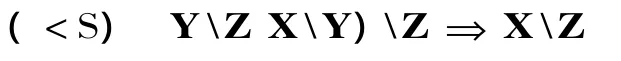
不僅如此，基于Jacobson(1990，1992)、Hepple(1990)、Baldridge(2002)和Baldridge＆Kruijff (2003)等人的工作，CCG進一步提出函子范疇及其規則的模態化概念，即給斜線算子添加下標。具體來說，CCG提出四個基本的模態＊，◇，×和■作為斜線算子的下標，各種不同下標的斜線算子適用于不同的函子范疇組合規則。換言之，不同下標的斜線算子的性質往往通過各自適用的組合規則體現出來。

提出斜線算子模態的用意在于:帶下標＊的斜線算子是最受限的，僅適用于最基本的函項應用規則(即NL的規則);帶下標◇的斜線算子允許推演中的結合性(即適用于L的規則);帶下標×的斜線算子允許推演中的交換性(即適用于NLP的規則);帶下標■的斜線算子適用于所有的范疇推演規則(即適用于LP系統的規則)［1］，見圖3:

圖3 斜線模態下標的作用

提出斜線算子模態下標的后果是給有關詞條指派帶下標的函子范疇，詞條在生成中受到的限制通過各自不同下標的斜線算子不同的適用范圍體現出來。如果不用模態下標，要避免某些不合語法的詞序(詞的線性排列)，我們不得不把各種自然語言生成中受限制或被禁止的地方專門列出來，從而使組合規則因自然語言的不同而異。采用模態下標的手段，組合規則就是普遍適用的，每一自然語言的語法適用同樣的規則集合，不同自然語言的差異表現在詞庫中，即有關詞條指派帶模態下標的函子范疇，這是CCG的特色。

四個模態下標的關系類似四個蘭貝克演算的關系:處于頂端的＊是最強的母類型，適用的組合規則范圍最窄;處于底端的 ■ 是最弱的子類型，適用的組合規則范圍最寬，見圖4。

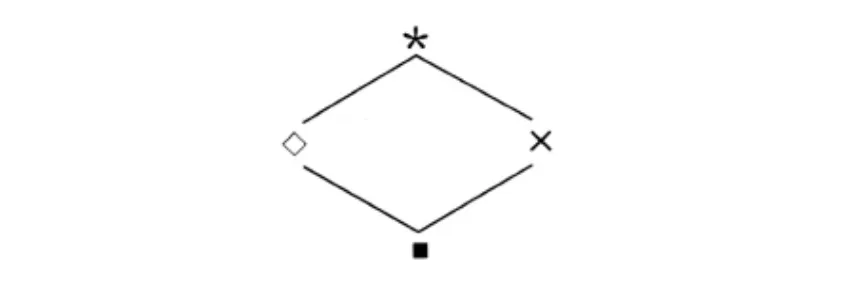
圖4 斜線模態下標之間的關系

帶下標＊的斜線算子適用的規則范圍最窄，只有少量的組合規則適用于帶下標＊的斜線算子，這包括范疇語法最基本的規則(＞)和(＜):

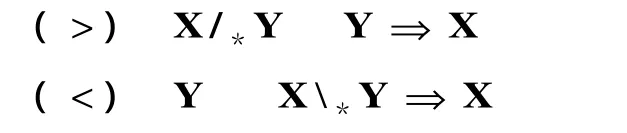
因為＊是其他模態下標的最大母類型，(＞)和(＜)之類斜線/＊涉及的規則適用于其他所有模態下標的范疇。即對任α∈{＊，◇，×，■}，X/αY Y?X總能成立。

以下組合規則對帶■的斜線算子范疇適用，但對＊不成立:

這些組合規則由于具有上述限制，我們就可以在詞庫中對英語連詞“and”指派帶＊的斜線算子范疇，以剔除那些不符合英語語法的生成推演，從而指出某些英語詞條的排列不合語法性。在詞庫中只要有(4)這樣的指派，(5)那樣的推演就不能獲得結果，(＜B)向后組合規則不適用于帶＊的斜線算子范疇。這就從CCG的角度解釋了“sleeps and he talks”的不合語法性。

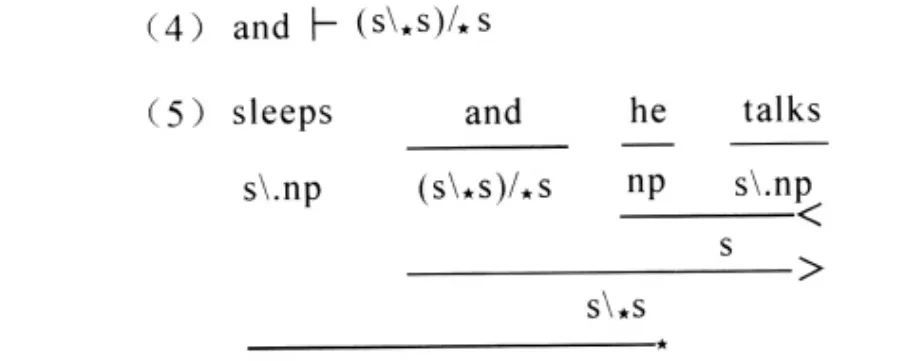
推而廣之，指派給“and”的范疇表現為:(X★X)/★X，這種指派能夠滿足英語中正常表達式的范疇推演，如圖5:

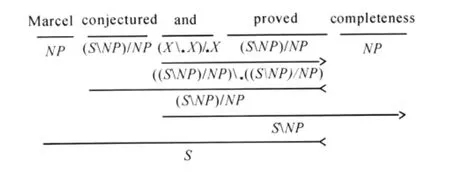
圖5 推演例

最后，我們簡略介紹CCG基于范疇等級概念和從范疇構造的視角建立的CCG證明論。CCG的英語片段思想和蒙太格語法略有不同，不同種類自然語言的區別在蒙太格語法那里通過句法規則體現出來，而CCG貫徹詞匯主義的思路把這些差異放到詞庫中去。CCG的證明論也不同于TLG的做法，而是從范疇構造的獨特視角建立的范疇推演理論［2］。

先介紹類型(范疇)等級(type hierarchy)的概念。類型的等級是序對〈T，?〉，滿足:

1)T是類型的字母表。

2)?是T上自返的反對稱的和傳遞的關系，稱作管轄關系，該系統是一個弱序。

3)〈T，?〉有一個最小元素(處于等級頂端的)，即存在一個類型管轄自身在內的所有類型。

4)〈T，?〉滿足:T的具有上限的每一子集都有一個最小上限。〈T，?〉中極大類型的集合中的元素是除自身外不管轄其他任何類型，換言之，極大類型是沒有(真)子類型的類型。

我們給出類型等級的例子，如圖6:

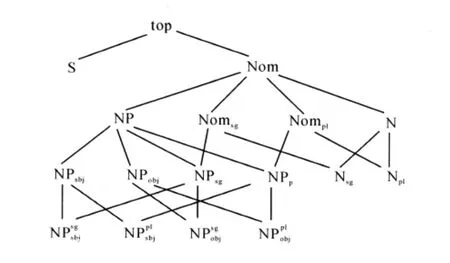
圖6 英語的范疇等級關系

直線條表示管轄關系?。top是該類型等級中的最小類型，它管轄該等級中所有的類型。是該類型等級中的極大類型，它們只管轄自身。T在這里作為飽和(原子)范疇的集合A有top，S，Nom等17個成員。

上述類型等級中只有飽和的原子范疇，這對刻畫自然語言的生成推演是不夠的。我們還需要大量的函子范疇，所以CCG就有函子范疇的構造(category structure)、函子范疇的描述(category description)以及前者對應后者的滿足等概念。

前面談到，指派給詞條的范疇，尤其是函子范疇的構造凝聚了有關的句法生成過程。

對范疇構造進行形式化定義就構成了CCG證明論的語義基礎。基于飽和(原子)范疇字母表A上的范疇構造是一個六元組〈Q，Res，Arg，Vs，VM，VA〉，其中:1)Q是點的集合;2)Res和Arg分別是Q上的結果關系和論元關系;3)Vs和VM對每一非終結點分別指派斜線和斜線的模態下標; 4)VA對每一終結點指派A中的一個飽和范疇。例如，基于字母表{S，NP}的函子范疇(S×(NP)/*(NP◇S)的構造樹為(見圖7):

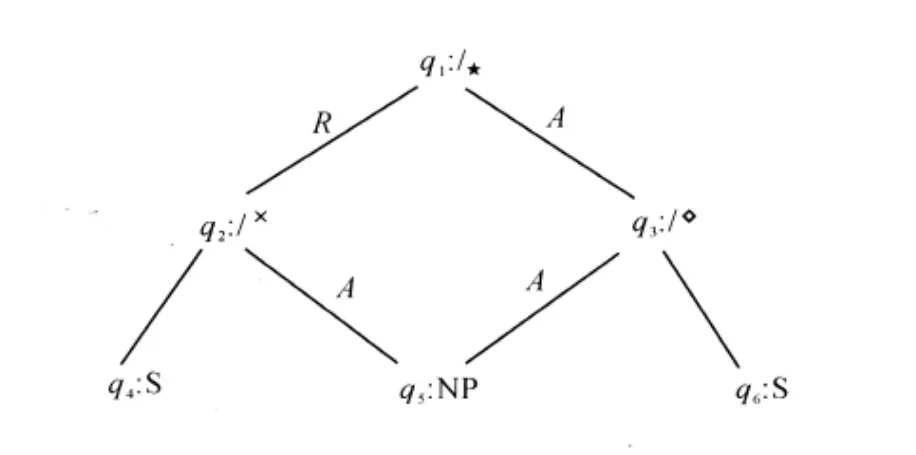
圖7 范疇構造樹

范疇構造是語義概念，相關的句法概念是范疇描述。范疇描述的集合是這樣一個最小的集合，滿足:

1)每一飽和范疇符號自身是范疇描述，即A?Φ;

2)對所有φ，ψ∈Φ，所有μ∈{＊，◇，×，■}，φ/μψ∈Φ;

3)對所有φ，ψ∈Φ，所有μ∈{＊，◇，×，■}，φ/μψ∈Φ;

4)對所有φ，ψ∈Φ，所有μ∈{＊，◇，×，■}，φ/μψ∈Φ。①這里出現的豎線雙方向算子在通常文獻中不常見，參見參考文獻［2］。

然后，令基于類型等級〈A，?〉的范疇構造S=〈Q，Res，Arg，Vs，VM，VA〉，q∈Q。S與q局部滿足A上的范疇描述φ，即S，q╞φ當且僅當

1)φ∈A:存在某個滿足 φ?α的 α使得VA(q)=α

2)φ=(ψ1δμψ2)，δ∈{/，}，μ∈{＊，◇，×}，Vs(q)=δ，VM(q)=μ，S，Res(q)╞ψ1并且S，Arg(q)╞ψ2

3)φ=(ψ1|μψ2)，μ∈{＊，◇，×}，VM(q)=μ，S，Res(q)╞ψ1并且S，Arg(q)╞ψ2

4)φ=(ψ1δ■μψ2)，δ∈{/，}，Vs(q)=δ，S，Res(q)╞ψ1并且S，Arg(q)╞ψ2

5)φ=(ψ1|■ψ2)，S，Res(q)╞ψ1，S，Arg(q)╞ψ2

基于上述英語范疇的等級，CCG給出英語片段，也叫英語部分語句系統的形式定義。令∑是英語詞條的集合，我們有∑基礎上的四元組〈A，?，S，L〉滿足:

1)〈A，?〉是飽和范疇的等級。

2)S是A中的特異元素。

3)L是從∑中非空符號串到A上生成的范疇描述的映射，即英語詞庫。

這樣的〈A，?，S，L〉就稱作CCG的英語片段。

最后，CCG給出任意兩個范疇描述φ和ψ的?－相容概念，在英語片段基礎上定義各種有效推理模式的概念:把詞庫中對詞條的范疇指派定義成前提詞條結論為范疇的推理模式;范疇的提升、不同模態下標的函子范疇的各種組合和置換規則自然就是CCG證明論中帶有各種不同限制條件的推理模式［2］。

所以，組合范疇語法CCG比較類型邏輯語法TLG而言，能更加深入揭示自然語言的語言學特點，全面服務于自然語言的計算機處理需求。其特征是:1)為刻畫自然語言詞類的豐富句法特征對原子范疇進行加標多樣化的設置;2)為描述自然語言句法生成的細微之處對斜線算子實行模態化分類，據此確立不同斜線算子范疇的多樣組合規則;(3)基于范疇等級和范疇構造的思想構造CCG的證明論系統。

［1］Steedman M，Baldridge J.Combinatory Categorial Grammar［C］//Kirsti B?rjars.Non－transformational syntax:a guide to current models.［S.l.］:Blackwell，2005.

［2］McConville，Mark.Type－hierarchical CCG［M］.Edinburgh:University of Edinburgh，2005.

Combinatory Categorial Grammar CCG

ZOU Chong－li1，2
(1.School of Humanities and Law，Yanshan University，Qinghuangdao 066004，China; 2.Institute of Philosophy，Chinese Academy of Social Sciences，Beijing 100732，China)

Combinatory Categorial Grammar(CCG)and Type Logical Grammar(TLG)are the modern version of the categorial grammar.The former approach is concerned with the application of the linguistics and the information processing of the natural language;and the later one tended to scrutinize the nature of the theory of categorial grammar from the perspective of logic.The features of CCG are: the various way of labeling the basic category and the complete lexicalism;the modalization to the index of the slash operator and the multiple combinations of functor categories;the proof to CCG which based on the class of category and the construction of category.

CCG;TLG;combination of functor categories

B81

A

1674－8425(2011)08－0001－05

2011－06－06

國家社科基金項目“面向自然語言信息處理的范疇類型邏輯研究”(09BZX046)研究成果。

鄒崇理(1953—)，男，四川成都人，研究員，博士生導師，研究方向:自然語言邏輯。

(責任編輯 魏艷君)