灰色線性回歸組合模型在湖北省老齡人口預測中的應用
胡 芬
(長江職業(yè)學院公共課部,湖北 武漢 430074)
胡 芬
(長江職業(yè)學院公共課部,湖北 武漢 430074)
人口老齡化是我國目前面臨的一個重大挑戰(zhàn)。老齡人口數(shù)是人口老齡化的一個重要參數(shù),研究老齡人口數(shù)的發(fā)展趨勢對分析人口老齡化過程十分重要。利用灰色-線性回歸組合模型對湖北省老齡人口進行了模擬,預測精度較高,說明用該組合模型對人口老齡化問題進行預測較合理。
人口老齡化;灰色預測;灰色關聯(lián)度;線性回歸模型
人口老齡化是人口年齡結(jié)構(gòu)變化、社會經(jīng)濟發(fā)展影響人口發(fā)展過程的必然產(chǎn)物,同時將對社會經(jīng)濟發(fā)展和未來人口變化產(chǎn)生深刻的影響。老齡化逐漸成為世界普遍關注的問題,預計21世紀人類將全面進入老齡社會,人口老齡化將是人類發(fā)展的主要特征。我國不僅是世界人口大國,老齡人口數(shù)也居全球老齡人口數(shù)之首,人口老齡化將成為21世紀困擾我國社會經(jīng)濟持續(xù)發(fā)展的突出問題。老齡人口數(shù)是人口老齡化的一個重要參數(shù)。因此,準確預測老齡人口數(shù)量及其增長,為中國經(jīng)濟和社會發(fā)展決策提供科學依據(jù),對于加速推進我國現(xiàn)代化建設的宏偉大業(yè)有著極為重要的現(xiàn)實意義。
然而,人口是極其復雜的系統(tǒng)。人口系統(tǒng)受到很多因素的影響,既有社會經(jīng)濟因素,自然環(huán)境因素,也有傳統(tǒng)習俗和思維方式方面的因素。這些因素之間的結(jié)構(gòu)關系相當復雜,且處于動態(tài)變化之中,其運行機制和變化規(guī)律以及它對人口變化的作用無法精確表達,這使得很難對老齡人口數(shù)做出較精確的預測。因此,構(gòu)建合適的預測方法對老齡人口數(shù)進行分析、模擬和預測具有特別重要的理論意義和實用價值。下面,筆者利用灰色-線性回歸組合預測模型進行預測。
1 灰色-線性回歸組合模型
我國學者鄧聚龍教授于1982年創(chuàng)立的灰色系統(tǒng)理論是以“部分信息已知,部分信息未知”的“小樣本”、“貧信息”為研究對象的不確定性系統(tǒng),它通過對“部分”已知信息的開發(fā)和生成去了解、認識現(xiàn)實世界,實現(xiàn)對系統(tǒng)運行行為和演化規(guī)律的正確把握和描述。灰色系統(tǒng)理論具有要求樣本數(shù)據(jù)少、原理簡單、運算方便、短期預測精度高、可檢驗等優(yōu)點,因此得到了廣泛的應用,并取得了令人滿意的效果。但是,它和其他預測方法一樣,也存在一定的局限性。所以近年來,許多學者都在深入研究灰色系統(tǒng)的特點,以充分發(fā)揮其模型優(yōu)勢。組合模型可以實現(xiàn)不同模型之間的功能和優(yōu)勢互補,避免單一模型在預測中的局限性,增強預測能力,改善預測精度。
1.1灰色關聯(lián)度模型
設X0={x0(tk),k=1,2,…,n}為參考序列,Xi={xi(tk),k=1,2,…,n}(i=1,2,…,m)為被比較序列。關聯(lián)度分析實質(zhì)上是分析曲線間幾何形狀的差別,因此將以曲線間的差值的大小作為關聯(lián)程度的衡量尺度。Xi與X0在tk時刻的關聯(lián)系數(shù)r0i(tk)定義為:
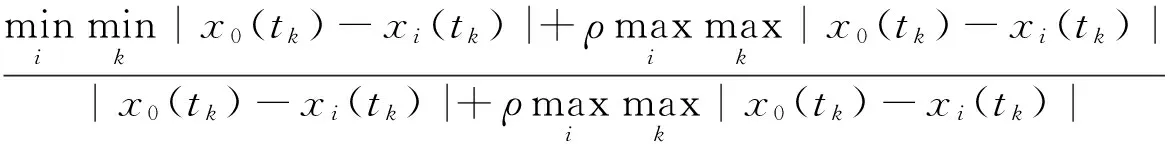
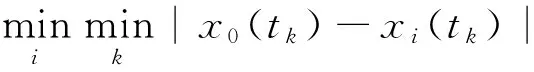
Xi與X0在tk時刻的關聯(lián)r0i定義為:
一般選取r0i>0.7的Xi作為進入多元線性回歸模型中的變量。
1.2多元線性回歸模型
在一般多元線性回歸模型中,因變量Y={Y1,Y2,…,Yq}(q為因變量個數(shù))和自變量X={X1,X2,…,Xm)(m為自變量個數(shù)),當數(shù)據(jù)總體滿足高斯-馬爾科夫定理時,由最小二乘法有:
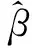
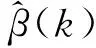
2 應 用
2.1數(shù)據(jù)選取
由于人口是一個較復雜的系統(tǒng),影響老齡人口數(shù)的因素也是錯綜復雜的。筆者根據(jù)老齡人口的特點結(jié)合中國統(tǒng)計年鑒,最終給出了以下8大因素:①國內(nèi)人口總數(shù)—X1(萬人);②湖北人口總數(shù)—X2(萬人);③GDP—X3(億元);④湖北省0~14歲人口數(shù)—X4(萬人);⑤湖北省15~64歲人口數(shù)—X5(萬人);⑥湖北省人口出生率—X6(%);⑦湖北省人口死亡率—X7(%);⑧湖北省人口自然增長率—X8(%)。
根據(jù)中國統(tǒng)計年鑒選取1996-2005年數(shù)據(jù)為參考數(shù)據(jù)序列,各因素原始數(shù)如表1所示。
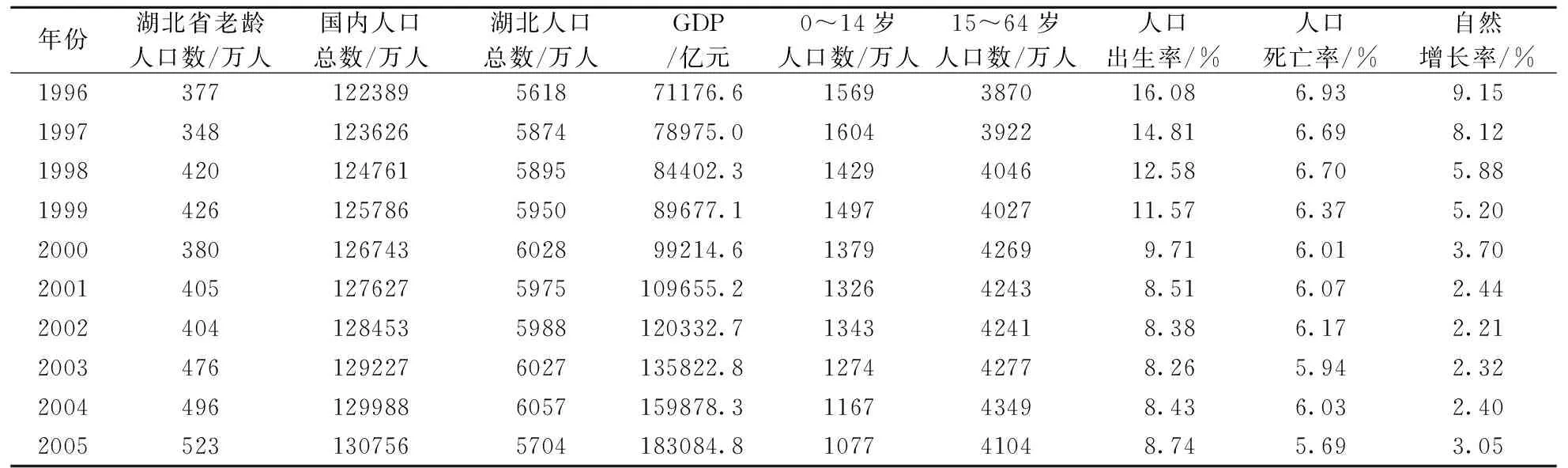
表1 湖北省老齡人口及其相關數(shù)據(jù)(1996~2005)
2.2模型的建立及預測
根據(jù)灰色關聯(lián)度的計算,求得湖北省老齡人口數(shù)與各因素之間的灰色關聯(lián)度如下:r01=0.85,r02=0.84,r03=0.65,r04=0.72,r05=0.86,r06=0.61,r07=0.75,r08=0.54 。則由關聯(lián)度的大小排序有:
r05>r01>r02>r07>r04>r03>r06>r08
關聯(lián)度的大小直接的反映了自變量與因變量之間關系緊密程度,關聯(lián)度大的說明其對因變量的影響較大,關聯(lián)度小的說明其對因變量的影響較小。通過上面的關聯(lián)度排序可以看出湖北省15~64歲人口數(shù)對老齡人口數(shù)的影響最大,而自然增長率對老齡人口數(shù)的影響最小。
筆者選取關聯(lián)度大于0.7為主要影響因素,小于0.7為次要影響因素。由此可知,影響老齡人口數(shù)的主要因素為湖北省15~64歲人口數(shù)、國內(nèi)人口總數(shù)、湖北人口總數(shù)、湖北省人口死亡率和湖北省0~14歲人口數(shù)。而次要因素為GDP、湖北省人口出生率和湖北省人口自然增長率。下面以老齡人口數(shù)為因變量、5個影響因素為自變量建立多元線性回歸模型。
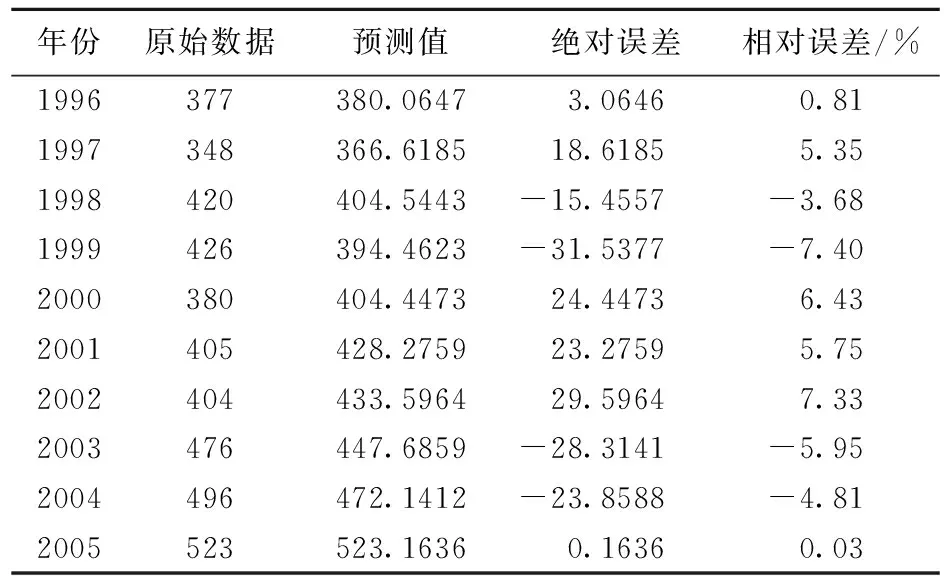
表2 模型的預測值及模型誤差
由嶺估計的簡易計算公式可得到模型的參數(shù)值,通過對不同的嶺參數(shù)k值所對應的參數(shù)及方差擴大因子的比較,筆者選取了k=0.1時的嶺估計作為最終的回歸模型參數(shù)的估計方法。當k=0.1時,回歸模型如下:
根據(jù)原始變量的回歸模型,表2給出了模型的預測值及模型誤差。通過表2可以看到,預測值與原始數(shù)據(jù)較接近,模型誤差僅為4.75%,說明模型的預測精度較高,而且2005年的相對誤差只有0.03%,結(jié)果十分滿意。
[1]鄧聚龍.灰色控制系統(tǒng) [M]. 第2版.武漢:華中科技大學出版社,1993.
[2] 杜鵬.人口老齡化與老齡問題:高級公務員讀本[M].北京:中國人民大學,2006.
[3] 陳玉光,張澤厚.中國人口結(jié)構(gòu)研究[M].北京:中國社會科學出版社,1984.
[編輯] 洪云飛
10.3969/j.issn.1673-1409.2011.05.004
O212.1
A
1673-1409(2011)05-0011-03

