高職院校《計算機數學基礎》改革探討

蔡俊娟 (廈門海洋職業技術學院，福建 廈門 361005)

高職院校《計算機數學基礎》改革探討

蔡俊娟 (廈門海洋職業技術學院，福建 廈門 361005)

《計算機數學基礎》是廈門海洋職業技術學院計算機科學與技術專業的必修課，是該專業一門核心基礎課，也是學習專業理論課不可缺少的數學工具。結合具體情況，從多方面闡述了該門課程重要性及改革的必要性，并提出了改革的具體措施。

高職教育；計算機數學；Mathematica

1 改革目標

《計算機數學基礎》[1]是廈門海洋職業技術學院計算機專業必不可少的專業基礎課程，是學習后續課程尤其是計算機專業課程不可或缺的數學工具。根據教育部《關于全面提高高等職業教育教學質量的若干意見》的精神和要求，學校在專業調研的基礎上，以計算機專業發展需要為依據，整合教學內容，從新的視角對計算機數學原有體系結構進行了優化，確立服務學生專業學習，面向學生就業的課程定位，在內容廣度上，遵循“以應用為目的，以必需夠用為度”，在內容體系的構架上，按專業需求設立模塊，模塊間相互獨立，形成理論與應用、知識與技能相融合的課程體系。這個設計理念既符合不同智能結構個體的學習，又符合高技能人才基本發展能力的培養要求。

理工科所通用的《高等數學》側重數學理論的分析，微積分等基礎知識，但是計算機主要處理的是離散問題，因此用《高等數學》中的教學內容來要求計算機系的學生，已經不再適應社會的進步。對高職院校的學生來說，計算機專業應該要把離散數學作為一個前期的基礎課程，它所提供的訓練，有利于學生抽象思維能力、邏輯推理能力、歸納構造能力的提高，有利于學生嚴謹、完整、規范的科學態度的培養。《計算機數學基礎》這門課程簡單介紹一元微積分的基本知識，借助數學軟件Mathematica弱化繁鎖的計算過程。同《高等數學》最大的不同，就是加入離散數學的部分知識，比如樹、圖、二叉樹等數據結構所需要處理到的知識點。當然，作為一名高職生，微積分知識也是相當重要的，所以必須微積分知識與離散數學知識并重。

2 改革措施

2.1增強教學中的互動性

傳統教學是以老師“講”為主的填鴨式教學，學生大多不感興趣，學習積極性與主動性不夠。在教學過程中，如果能夠增強師生之間的互動性，會提高學生的學習熱情，達到意想不到的教學效果。如在學習逆矩陣的時候，學生對于枯燥的計算過程表現出十分厭煩的情緒，可以“利用矩陣來設置密碼”這個案例來吸引學生的興趣。首先，將一個3階的可逆矩陣作為密碼；其次將上課班級中一個學生名字的拼音字母對應字母表轉化成數字(表1，如莊毅林:ZHUANG Yi-lin轉化為數字分別為26，8，21，1，14，7，25，9，12，9，14，0)。

表1 字母與數字轉換表

2.2引入數學建模的思想

數學建模是一種數學的思考方法，是運用數學的語言和方法，通過抽象、簡化建立能近似刻畫并“解決”實際問題的一種強有力的數學手段[2]。高職學生大部分數學基礎較差，因此數學選題盡量貼近現實生活，使學生不斷感受到數學在現實中的應用途徑和方法，借助計算機成功解決實際問題，以提高學生的成就感，增加對該門課程的學習熱忱。

2.3教學方法改革

1)強化“翻譯”功能 在學生第1次接觸該課程的時候，筆者問學生覺得該門課程應該學習哪些內容，學生答案五花八門，但是大部分人認為計算機數學應該是繁鎖的計算過程和深奧的數學理論，普遍存在畏難心理。但是筆者告訴學生這門課程其實就是一個“翻譯”的學科，是將現實生活中發生的一些現象“翻譯”成數學語言，再將數學公式“翻譯”成計算機語言，交給計算機處理得到實際問題的解決方案，學生覺得很有意思，不再對“數學”課程感到排斥。

2)淡化系統性 針對大部分學生基礎的普遍薄弱性，在介紹概念的時候，不再要求學生掌握嚴格的數學定義，而是通過案例的引入，要求學生對概念的理解，盡可能減少學生對定義的抽象感。在講解運算法則和規律時，用精簡有趣的語句幫助學生記憶，避免符號復雜，加強對數學公式的理解。

3)加強上機操作 在該課程的學習中，要求學生安排一定課時的上機操作，學習Mathematica軟件[3-4]。通過計算機數學實驗進行數值、圖形、動畫演示，使概念更清楚，原理更明白。如用Mathematica演示微積分第一基本定理的過程如下：

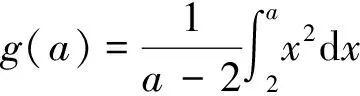
g[a_]=1/(a-2)Integrate[x2,{x,2,a}] able[g[a],{a,2.3,2.001,-0.001}]

(II)圖形演示。畫出函數g[a]的圖形，從圖形上觀察a趨向于2時函數g[a]的變化趨向，即趨向于f(2)。輸入命令：Plot[g[a],{a,-1,3}]，執行即可得到結果。通過上述例子，可以加深學生對微積分基本公式的理解與記憶，并增強學生的實際動手能力。

2.4考核方式改革

把考核貫穿于《計算機數學基礎》學習的全過程，隨時隨地記錄學生的成長，口頭與書面相結合，課內與課外相結合，過程與結果相結合。總評分數由以下幾部分組成：期考的閉卷考試占40%，著重計算機數學理論部分知識的考核；上機操作考核占20%，這部分強調學生的動手能力；論文占10%，這部分是考核學生的數學建模思想以及團隊協作的能力；平時表現占10%，綜合學生作業、考勤及課堂表現進行綜合測評。這種方式取得了較好的效果。

[1]劉樹利，王家玉.計算機數學基礎[M].第2版.北京：高等教育出版社，2004.

[2]葉其孝，姜啟源.數學建模[M].北京：機械工業出版社，2010.

[3]李亞杰，黃根隆.數學實驗[M].北京：高等教育出版社，2004.

[4]鄧建松，彭冉冉.Mathematica使用指南[M].北京：科學出版社，2002.

[編輯] 洪云飛

10.3969/j.issn.1673-1409.2011.07.042

N4

A

1673-1409(2011)07-0120-02

2011-05-28

蔡俊娟，女，碩士，講師，現主要從事概率論與數理統計方面的教學與研究工作。