關于定積分微元法的一點補充

佘智君

（貴州大學理學院基礎教學部，貴州貴陽 550003）

關于定積分微元法的一點補充

佘智君

（貴州大學理學院基礎教學部，貴州貴陽 550003）

通過一個實例提出問題，進而給出微元法中推導微元及檢驗微元表達式的簡便方法.［關鍵詞］定積分；微元法；微分

1 引 言

《數學分析》和《高等數學》教材都介紹了微元法，應用微元法可將一些幾何、物理等實際問題轉化為定積分來求，而微元又是微元法的關鍵，能否合理選擇所求量的微元，關系到所求量的正確性，那么究竟如何選擇微元才能保證所取微元是合理的呢？學生經常感到困惑，以致于他們只能模仿例題“機械地套用”微元法.在“微元法”中，我們經常用直線段代替曲線段，以不變量代替變量，以均勻代替不均勻，那么是否直觀上近似的量都可以作為所求量的微元呢？我們先看下面的例子.

設曲線y＝f（x）＞0是［a，b］上的光滑曲線，求該曲線繞x軸旋轉一周所得旋轉曲面的面積.

在直觀上看，當d x→0時，在［x，x＋d x］上切線段AB≈弧，直線段≈弧，那么切線段及直線段分別繞x軸旋轉一周所得小扁圓臺的側面積是否都可以作為所求旋轉曲面面積的微元d A呢？現記切線段＝d s，直線段＝d x.

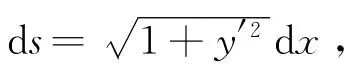
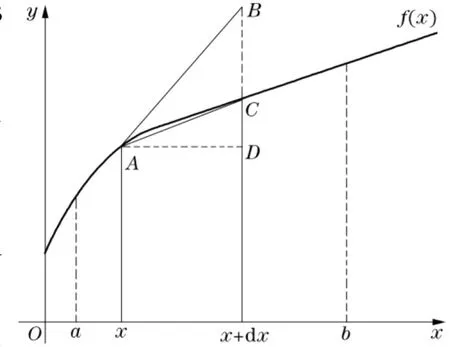
圖1

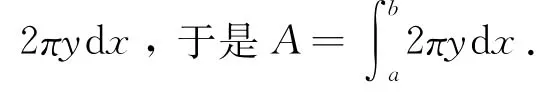
同一旋轉曲面的面積，怎么會出現兩個不同結果呢？這其中之一一定有誤，問題又出在哪呢？

2 微元法的條件及證明

2.1 一般地，若所求量U滿足下列條件：

（i）U是與某個變量x的變化區間［a，b］有關的量；

（ii）U對區間［a，b］具有可加性；

（iii）將區間［a，b］分成若干小區間，取其中任一小區間［x，x＋d x］，如果對應于區間［x，x＋d x］的部分量ΔU能近似地表示為［a，b］上的一個連續函數在x處的函數值f（x）與d x的乘積，且ΔU＝f（x）d x＋o（d x），稱f（x）d x為量U的微元，記作：d U，即d U＝f（x）d x，則U＝f（x）d x.上述方法稱為定積分的微元法.

這時我們會提出以下問題：

2.2 為什么ΔU＝f（x）d x＋o（d x）就有U＝f（x）d x？

關于該問題，《數學分析》和《高等數學》教材都沒有作理論的論證，對此本文將作如下推導：

記U（x）＝U［a，x］，顯然U（a）＝0，U［a，b］＝U.

因為ΔU＝f（x）d x＋o（d x），所以由微分的定義有d U＝f（x）d x，于是U′（x）＝f（x），再由牛頓-萊布尼茨定理得

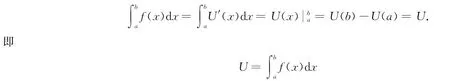
2.3 如何檢驗ΔU＝f（x）d x＋o（d x）？

因為f（x）是要求的連續函數，也就是說U是未知的，所以要嚴格檢驗ΔU＝f（x）d x＋o（d x）是非常困難的，對此給出如下命題：

命題 設f（x）在［a，b］上連續，U是一個與區間［a，b］有關的量，且U對區間［a，b］具有可加性，若對區間［a，b］上的任意小區間［x，x＋d x］有

其中M，m分別是f（x）在區間［x，x＋d x］的最大、最小值，則

該命題的（＊）式在許多實際問題中是可直觀看出的，這樣它不僅給出了如何求微元中的連續函數f（x），而且還克服了ΔU＝f（x）d x＋o（d x）不可直接檢驗的問題.

3 總 結

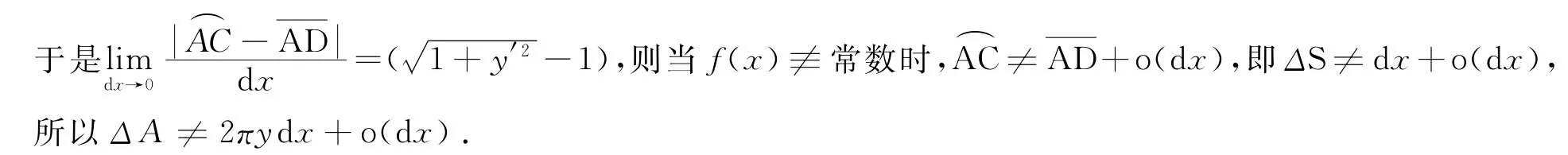
因此第二種解法是錯誤的，錯誤的根源在于忽略了微元的條件ΔU＝f（x）d x＋o（d x），誤認為只要是所求量的近似量就可作為它的微元，所以應用微元法解決實際問題時，要特別注意其條件ΔU＝f（x）d x＋o（d x），在教學中應強調微元法的關鍵是根據實際問題確定被積函數f（x），從而正確的寫出所求量的微元，把教學生如何找所求量的微元作為重點.

［1］ 同濟大學數學教研室.高等數學（上冊）［M］.4版.北京：高等教育出版社，2000.

［2］ 陳傳璋，金福臨，朱學炎，歐陽光中.數學分析（上冊）［M］.2版.北京：高等教育出版社，1995.

［3］ 陳玉，賀秋林.微元法原理探究［J］.工科數學，2001，17（3）：95-96.

A Supplement on Differential Element Method of Definite Integral

SHE Zhi-jun
（Department of Basic Sciences，Guizhou University，Guiyang，550003，China）

A question is proposed by aconcrete example，and we propose simple method for the deriving and detection of the differential expression.

definite integral；method of differential element；differential

O172

C

1672-1454（2011）04-0176-03

2008-09-26