探索以(Fn-k,Fn,Fn)為邊長(zhǎng)的Fibonacci三角形

郝 鋒

(江蘇大學(xué)理學(xué)院,江蘇鎮(zhèn)江 212013)

探索以(Fn-k,Fn,Fn)為邊長(zhǎng)的Fibonacci三角形

郝 鋒

(江蘇大學(xué)理學(xué)院,江蘇鎮(zhèn)江 212013)

Fibonacci三角形是邊長(zhǎng)為Fibonacci數(shù)、面積為整數(shù)的三角形.存在以(Fn-k,Fn,Fn)為邊長(zhǎng)的Fibonacci三角形的情形可以被劃分為三類(k＜n),利用平方剩余的方法可以證明：k=2t+2時(shí),不存在邊長(zhǎng)為(Fn-k,Fn,Fn)的Fibonacci三角形.

Fibonacci數(shù);Lucas數(shù);Fibonacci三角形

Fibonacci數(shù)列{Fn}為F0=0,F1=1,Fn+2=Fn+1+Fn.與之關(guān)系密切的Lucas數(shù)列{Ln}為L(zhǎng)0= 2,L1=1,Ln+2=Ln+1+Ln.可以利用其通項(xiàng)公式引入負(fù)指標(biāo)F-n=(-1)n-1Fn,L-n=(-1)nLn,仍滿足上述遞推關(guān)系[6].

邊長(zhǎng)為Fibonacci數(shù)、面積為整數(shù)的三角形,稱之為Fibonacci三角形.目前已知[1-7]：當(dāng)k≤7, k=2t·3或n≤11117時(shí)不存在邊長(zhǎng)為(Fn-k,Fn,Fn)的Fibonacci三角形.本文將存在以(Fn-k,Fn,Fn)為邊長(zhǎng)的Fibonacci三角形的情形劃分為三類(k＜n),并證明：k=2t+2時(shí),不存在邊長(zhǎng)為(Fn-k,Fn,Fn)的Fibonacci三角形.本文中字母未特別說(shuō)明的都為正整數(shù),X2表示某一完全平方數(shù).

1 預(yù)備知識(shí)

引理1 2Fm+n=FmLn+FnLm, L2n-5F2n=4(-1)n,L2n=L2n+2(-1)n-1;

特別地,

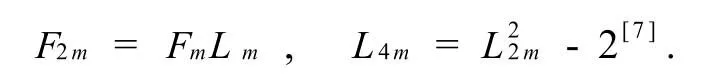
引理2 Fm+n=FmFn+1+Fm-1Fn,(Fm,Fn)=F(m,n).

引理3 L2t≡-1(mod4),-1是L2t的平方非剩余;

L2t+1≡-1(mod8),-2是L2t+1的平方非剩余[7].

引理4 當(dāng)q≡1(mod6)時(shí),Lq≡1(mod4);當(dāng)q≡-1,±2(mod6)時(shí),Lq≡-1(mod4);當(dāng)q≡0(mod6)時(shí),Lq≡2(mod4);當(dāng)q≡3(mod6)時(shí),Lq≡0(mod4).

證容易驗(yàn)證：Lq≡Lq+6(mod4).

引理5 當(dāng)3q時(shí),Fm+2pq≡(-1)p(q-1)Fm(modLq).特別地,當(dāng)3q時(shí),

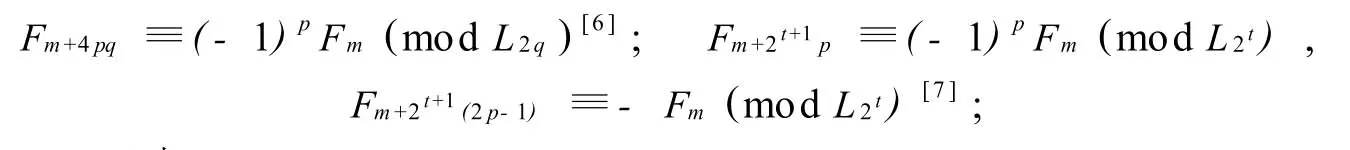
當(dāng)q≡-1(mod6)時(shí),Fm+2pq≡Fm(modLq).

當(dāng)p=4時(shí),T=6;當(dāng)p=8時(shí),T=12;當(dāng)p=3時(shí),T=8,p的平方非剩余2(modp);當(dāng)p=9時(shí), T=24,p的平方非剩余2,3,5,6,8(modp);當(dāng)p=7時(shí),T=16,p的平方非剩余3,5,6(modp);當(dāng)p=23時(shí),T=48,p的平方非剩余5,7,10,11,14,15,17,19,20,21,22(modp);當(dāng)p=11時(shí),T=10 ,p的平方非剩余2,6,7,8,10(modp);當(dāng)p=5時(shí),T=20,p的平方非剩余2,3(modp);…;當(dāng)p= L2t(t≥2),T=2t+2,-1和-2(modp)是平方非剩余;當(dāng)p=ft時(shí),T=2t+3·3,-1和-2(modp)是平方非剩余.

2 主要結(jié)果

如果存在以(Fn-k,Fn,Fn)為邊長(zhǎng)的Fibonacci三角形(k＜n),容易得到Fn-k為偶數(shù)(3|n-k),底邊上的高h(yuǎn)為整數(shù);記

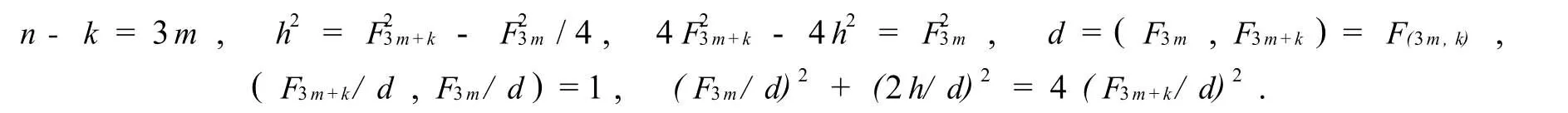
考慮(mod4),F3m/d必為偶數(shù).于是F3m/(2d)為整數(shù),(F3m+k/d,F3m/(2d))=1.對(duì)(F3m+k/d)2= (F3m/(2d))2+(h/d)2應(yīng)用商高定理,存在一奇一偶的正整數(shù)a和b,(a,b)=1,F3m+k/d=a2+b2,于是F3m+k/d≡1(mod4),F3m+k≡d(mod4)[7].

若m為奇數(shù),記m=4i±1,F3m=F12i±3≡2(mod4),F3m/2為奇數(shù);F3m/(2d)為整數(shù),d =F(12i±3,k)必為奇數(shù),3(12i±3,k),3k;F3m/(2d)為奇數(shù),于是存在一奇一偶的a和b使得F3m+k/d=a2+b2,F3m/(2d)=a2-b2,即F3m+k/d±F3m/(2d)=2a2和2b2;d為奇數(shù),F3m+k± F3m/2=2da2和2db2,正好是2的倍數(shù)和8的倍數(shù),F3m+k-F3m/2≡4(mod8)是不成立的.

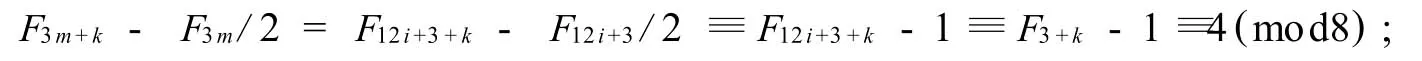
當(dāng)k≡8,10,11(mod12),3m=12i-3時(shí),

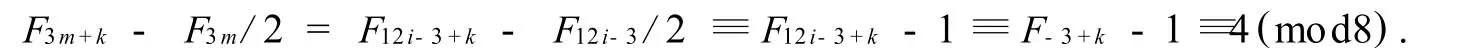
故可能的情形為k≡2,4,5(mod12),3m=12i-3,或k≡8,10,11(mod12),3m=12i+3.

①當(dāng)k≡2,4,5(mod12)時(shí),2F12i-3+k/d±F12i-3/d=X2,其中d=F(12i-3,k);當(dāng)k≡8,10,11 (mod12)時(shí),2F12i+3+k/d±F12i+3/d=X2,其中d=F(12i+3,k);

②F6i+k≡d(mod4),F6i+k/d±F6i/(2d)=X2,其中d=F(6i,k),3k;若m為偶數(shù),3|k,但6k.

i)記m=4i-2,F3m+k=F12i-6+k≡2(mod4),d=F(12i-6,k),d/2為奇數(shù);F3m/8=F12i-6/8為奇數(shù),F3m/(4d)為奇數(shù).于是存在一奇一偶的a和b,使得F3m/(2d)=2ab,F3m/(4d)=ab為偶數(shù),矛盾;

ii)記m=4i,F3m+k=F12i+k≡2(mod4),d=F(6i,k),d/2為奇數(shù);F3m=F12i≡0(mod16), F3m/(4d)為偶數(shù).于是F3m+k/d=a2+b2,F3m/(2d)=2ab,即F12i+k/d±F12i/(2d)=(a+b)2和(a-b)2.于是,當(dāng)3|k,6k時(shí),存在以(F3m,F3m+k,F3m+k)為邊長(zhǎng)的Fibonacci三角形必為如下情形：

③F12i+k/d±F12i/(2d)=X2,其中d=F(12i,k),3|k、6k.

若m為偶數(shù),6|k,記k=2t·3p,m=2sq,3m=2s·3q,其中p和q是奇數(shù).

i)若s≤t,d=F(3m,k)=F2s·3(q,p),F3m/2s+2為奇數(shù),d/2s+2為奇數(shù),故F3m/d為奇數(shù),與F3m/d為偶數(shù)矛盾;

ii)若s=t+1,則d=F(3m,k)=F2t·3(q,p),F3m/2s+2=F3m/2t+3為奇數(shù),d/2t+2為奇數(shù),故F3m/(2d)為奇數(shù).于是F3m+k/d=a2+b2,F3m/(2d)=a2-b2,即2F3m+k/d±F3m/d=4a2和4b2;

iii)若s=t+2,則d=F(3m,k)=F2t·3(q,p),F3m/2s+2=F3m/2t+4為奇數(shù),d/2t+2為奇數(shù),故F3m/(4d)為奇數(shù).于是存在一奇一偶的a和b,使得F3m/(2d)=2ab,F3m/(4d)=ab為偶數(shù),矛盾;

iv)若s＞t+2,則d=F(3m,k)=F2t·3(q,p),F3m/2s+2為奇數(shù),d/2t+2為奇數(shù),故F3m/(2s-td)為奇數(shù),F3m/(4d)為偶數(shù).于是F3m+k/d=a2+b2,F3m/(2d)=2ab,即F3m+k/d±F3m/(2d)=(a+b)2和(a-b)2.從而當(dāng)6|k時(shí),存在以(F3m,F3m+k,F3m+k)為邊長(zhǎng)的Fibonacci三角形必為如下情形：

④s-t=1時(shí),2F2s·3q+2t·3p/d±F2s·3q/d=X2,其中p和q是奇數(shù),d=F2t·3(p,q);

⑤s-t＞2時(shí),F2s·3q+2t·3p/d±F2s·3q/(2d)=X2,其中p和q是奇數(shù),d=F2t·3(p,q).

是否存在以(F3m,F3m+k,F3m+k)為邊長(zhǎng)的Fibonacci三角形需要排除上述三種情況(5種情形)的可能性,可以考慮不斷地選取合適的p用平方非剩余(modp)來(lái)排除,合適的選取次序?yàn)閜=4;3,9;7, 23;5,11;….特別要注意p=L2t+1或ft.

定理當(dāng)k=2t+2時(shí),不存在以(F3m,F3m+k,F3m+k)為邊長(zhǎng)的Fibonacci三角形.

證k=2t+2時(shí),

情形① d=F(12i±3,k)=F1=1,當(dāng)t為奇數(shù)時(shí),k≡8(mod24),2F12i+3+k±F12i+3=X2;當(dāng)t為偶數(shù)時(shí),k≡-8(mod24),2F12i-3+k±F12i-3=X2;

情形② F6i+k/d±F6i/(2d)=X2,其中d=F(6i,k)=F2(i,k/2)=F2,F4,…,Fk.

①i)當(dāng)t為奇數(shù)時(shí),8|k,2F12i+3+k±F12i+3不全是平方剩余,2F24j+3+k-F24j+3≡2F3-F3≡2(mod3);k=8(t=1)時(shí),

②記i=2u-1j(j為奇數(shù)),6i=2u3j,則4dF6i+k±2dF6i=4d2X2,其中d=F(6i,k)=F(2u,2t+2);

i)當(dāng)t為奇數(shù)時(shí),k≡8(mod24).若d=F22s,d≡F4≡3(mod4),但F6i+k≡Fk≡F2≡1(mod4),與F6i+k≡d(mod4)矛盾;若d=F2=1,u=1,i=j,4F6j+k±2F6j=4X2,但4F6j+k±2F6j不全是平方剩余,

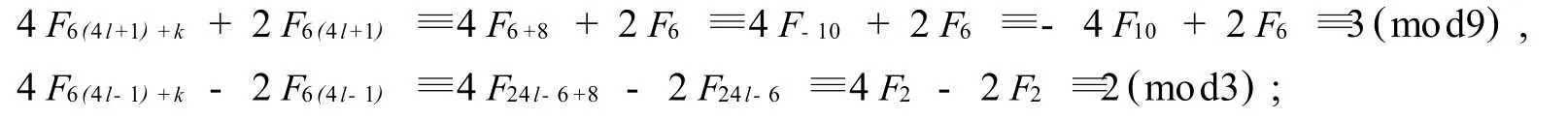
ii)當(dāng)t為偶數(shù)時(shí),k≡-8(mod24).若d=F22s-1,d≡F2≡1(mod4),但F6i+k≡Fk≡F4≡3(mod4),與F6i+k≡d(mod4)矛盾;綜上所述,u≥2.

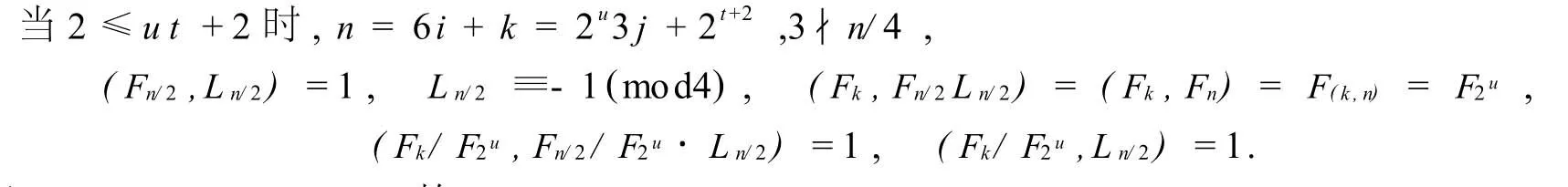
由于u≤t+1,F2u|Fn/2,故

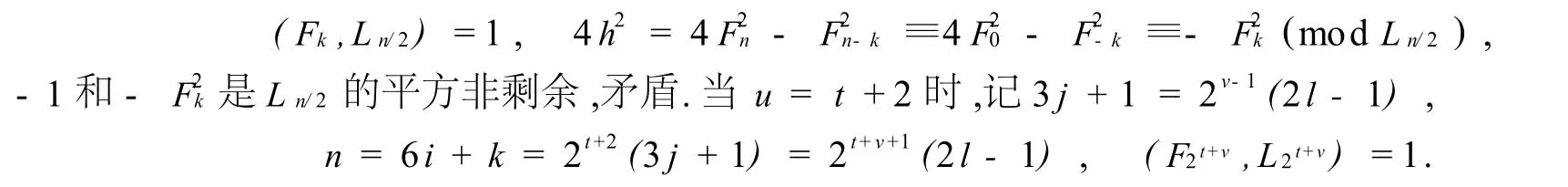
由于Fk|F2t+v,故(Fk,L2t+v)=1,4h2=4F2n-F2n-k≡4F20-F2-k≡-F2k(modL2t+v).-1和-F2k是L2t+v的平方非剩余,矛盾;當(dāng)t+2＜u時(shí),t+2≤u-1,Fk|F2u-1.由于(F2u-1,L2u-1)=1,故(Fk,L2u-1)=1,

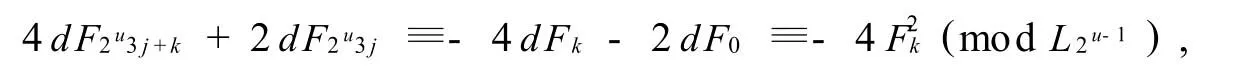
-1和-4F2k是L2u-1的平方非剩余,矛盾.

3 后 記

目前已解決了k=2t·3或2t+2時(shí)的情形,對(duì)于k＜24的其它情形可以按照k的三種情形分別解決,有關(guān)結(jié)果另文發(fā)表;對(duì)于k較大的其它情形有待于繼續(xù)研究.

[1] Harborth H,Kemnitz A.Fibonacci triangles[M].Kluwer Acad.Publ.,1990：129-132.

[3] Harborth H,Kemnitz A,Robbins N.Non-existence of Fibonacci triangles[J].Congr.Numer.,1995,114,29-31.

[3] 牟善志,劉華.Fibonacci三角形[J].數(shù)學(xué)的實(shí)踐與認(rèn)識(shí),2005(2)：149-151.

[4] 何波,吳文權(quán).關(guān)于Fibonacci三角形猜想k=6的證明[J].大學(xué)數(shù)學(xué),2007,23(5)：160-162.

[5] 林麗娟.關(guān)于Fibonacci三角形猜想k=7的證明[J].重慶工商大學(xué)學(xué)報(bào)(自然科學(xué)版),2007,24(5)：439-441.

[6] 柯召,孫琦.談?wù)劜欢ǚ匠蘙M].上海：上海教育出版社,1980：73-79.

[7] 郝鋒.k=2t·3時(shí)不存在邊長(zhǎng)為(Fn-k,Fn,Fn)的Fibonacci三角形[J].大學(xué)數(shù)學(xué),2011,27(1)：45-47.

Research Fibonacci Triangles with Side Lengths(Fn-k,Fn,Fn)

HAO Feng
(Faculty of science,Jiangsu University,Zhenjiang,Jiangsu 212013,China)

A triangles with side lengths of Fibonacci numbers and integral area are called Fibonacci Triangles.The existence of Fibonacci triangles with side lengths(Fn-k,Fn,Fn)can be partitioned three cases and non-existence of Fibonacci triangles(Fn-k,Fn,Fn)ofk=2t+2is proved with the method of quadrate residue(k＜n).

Fibonacci numbers;Lucas numbers;Fibonacci triangles

O156.1

A

1672-1454(2011)03-0106-04

2008-04-30