貨幣時間價值中插值圖示法的運用

內蒙古財經學院 郭巧莉 王彥東

貨幣時間價值中插值圖示法的運用

內蒙古財經學院 郭巧莉 王彥東

一、貨幣時間價值的本質

貨幣時間價值是指貨幣經過一定時間的投資和再投資所增加的價值，也稱為資金的時間價值。貨幣之所以有時間價值，其核心思想主要反映了貨幣作為一種特殊商品的稀缺性特點，它體現了是否使用貨幣的機會成本。西方財務理論認為，貨幣時間價值是對讓渡貨幣使用權而對貨幣擁有方的一種補償，它是天然的，是貨幣擁有者推遲現時消費而取得的一種價值補償。貨幣時間價值的表現形式主要有終值和現值，時間價值原理揭示了在不同時點上現金流量之間的等值換算關系即運用現值和終值公式計算現金流量在其收付時點與任何另一時點之間的等值價值轉換。

二、插值圖示法的引入

財務管理中貨幣時間價值的計算主要涉及現值、終值、年金、利率及期數等形式，一般現值、終值系數可通過對應整數形式的利率及期數查出來，然而系數表的使用范圍有限，教學中通常引入插值法。數學上插值法原理：假設“利率”或“期數”與相關的系數是在較小的范圍內呈直線關系，因此所求的利率i、期數n或系數，可根據兩組臨界值i1和i2、n1和n2或系數的關系通過構造相似三角形計算出來。插值法只能用在內插，插值函數都是在臨界點范圍內建立的，超出這個范圍，就很難保證有準確的結果，所以插值法通常又叫內插法。在財務管理的計算中使用插值法，如果僅用函數式來求解，對學生而言有點抽象，但是如果配以圖示法，學生會很直觀而輕松地化解疑問，本文對貨幣時間價值中的相關計算稱為插值圖示法。

三、貨幣時間價值計算中插值圖示法的運用

以下對貨幣時間價值計算的運用做一盤點，并舉例說明插值圖示法的運用。

其一，已知年金、終值、現值和期數，求利率。

［例1］現在向銀行存入5000元，在利率為多少時，才能保證在今后10年中每年得到750元？

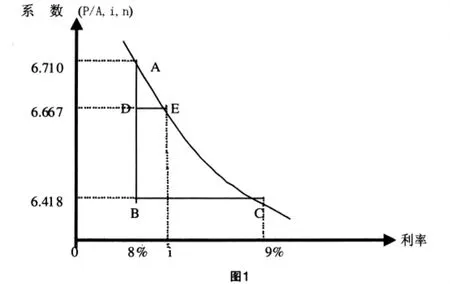
［例2］假設某公司決定從今年留存收益中提取20000元進行投資，希望5年后能得到2.5倍的錢用來對原生產設備進行技術改造。那么該公司在選擇這一方案時，所要求的投資報酬率必須達到多少？

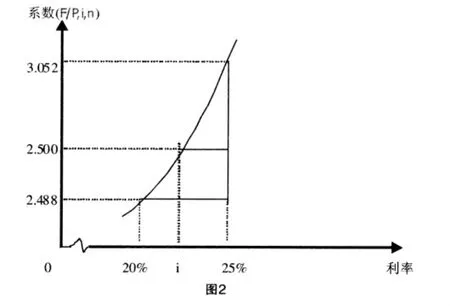
解析：20000×（F/P，i，5）＝2.5×20000，（F/P，i，5）＝2.500。查復利終值系數表找臨界值，（F/P，20%，5）＝2.488，（F/P，25%，5）＝3.052，用插值圖示法求解如圖2所示：

函 數 F/P，i，n＝（1+i）n是 增 函 數 ， 其 余 原 理 同 例 1，由

其二，已知期數、利率，求系數。

［例3］B公司計劃發行一種兩年期帶息債券，面值為100元，票面利率為6%，每半年付息一次，到期一次償還本金，債券的市場利率為7%。求該債券的公平價格。

解析：該債券半年付息一次，利息為3元（100×6%÷2），半年期的市場利率為3.5%（即7%÷2）。債券價格P＝100×3%×（P/A，3.5%，4）＋100×（P/F，3.5%，4），式中年金現值系數（P/A，3.5%，4）、復利現值系數（P/F，3.5%，4）無法通過查表取得結果，借助臨界值（P/A，3%，4）＝3.717（P/A，4%，4）＝3.630，（P/F，3%，4）＝0.888、（P/F，4%，4）＝0.855，用插值圖示法求解（P/A，3.5%，4）、（P/F，3.5%，4）如圖3所示：

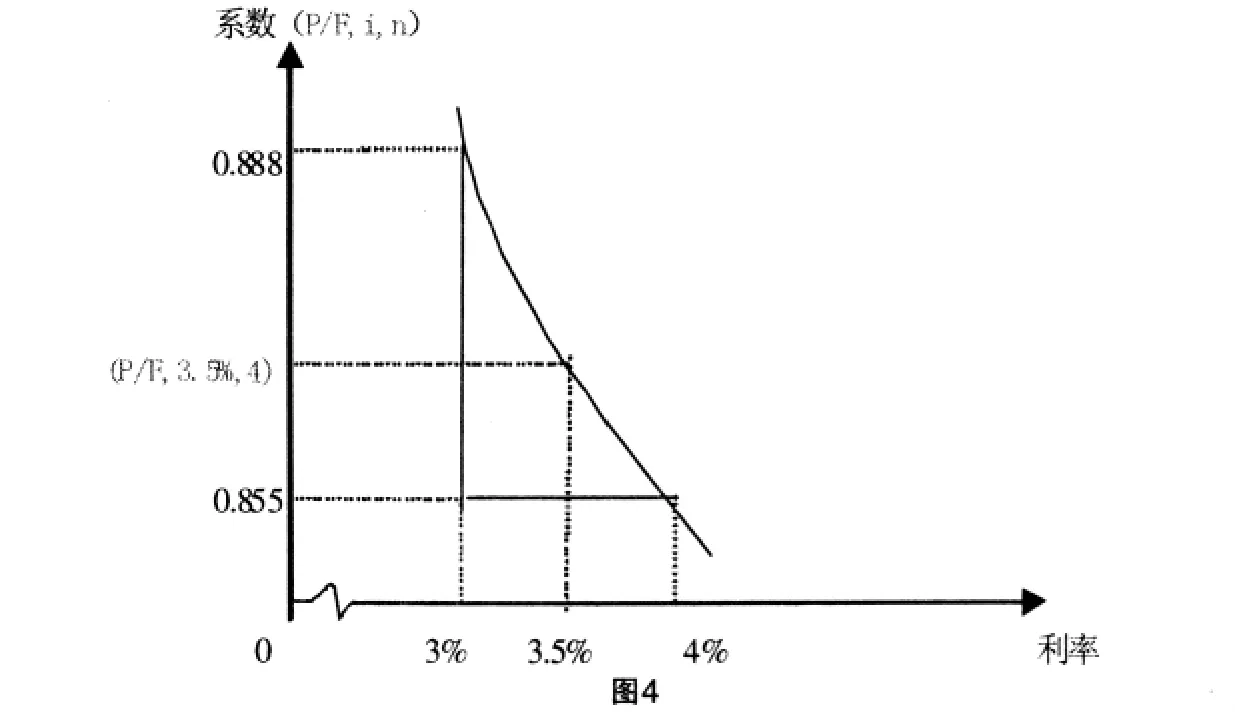
其三，已知利率、系數，求期數。

［例4］假設某公司決定提取140000元準備興建一棟倉庫。根據施工單位按圖紙估算，預算整個工程需要300000元。如銀行存款利率為8%，每年復利一次。那么需要存多少年才能獲得建倉庫所需要的資金？

解析：由140000×（F/P，8%，n）＝300000，（F/P，8%，n）＝當i＝8%、（F/P，8%，n）＝2.143時，復利終值系數表中沒有對應的整數n，所以需要用插值圖示法來求解n。找i＝8%時2.143的臨界值（F/P，8%，9）＝1.999，（F/P，8%，10）＝2.159，用插值圖示法求解如圖5所示：

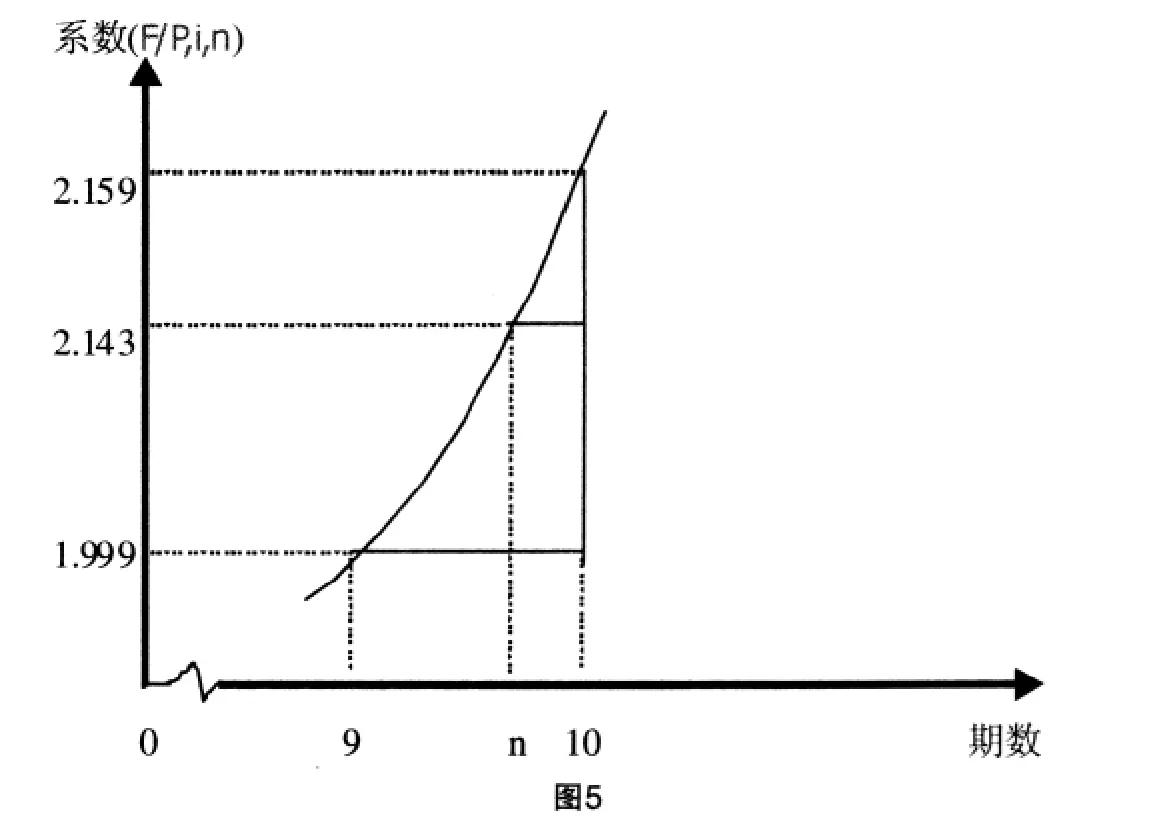
總之，每門課程都有其學習技巧與理解角度，只要善于歸納總結，棘手的問題也容易化解。

［1］王斌：《財務管理》，中央廣播電視大學出版社2002年版。

［2］徐焱軍：《相似三角形原理在<財務管理>課程中的應用》，《財會通訊》2005年第5期。

（編輯 杜昌）