雙障礙問(wèn)題的弱解的高階可積性

胡振華，周樹(shù)清，彭冬云

（1.湖南城市學(xué)院數(shù)學(xué)與計(jì)算機(jī)學(xué)院，中國(guó)益陽(yáng) 413000;2.湖南師范大學(xué)數(shù)學(xué)與計(jì)算機(jī)科學(xué)學(xué)院，中國(guó)長(zhǎng)沙 410081）

雙障礙問(wèn)題的弱解的高階可積性

胡振華1，2，周樹(shù)清2*，彭冬云2

（1.湖南城市學(xué)院數(shù)學(xué)與計(jì)算機(jī)學(xué)院，中國(guó)益陽(yáng) 413000;2.湖南師范大學(xué)數(shù)學(xué)與計(jì)算機(jī)科學(xué)學(xué)院，中國(guó)長(zhǎng)沙 410081）

通過(guò)構(gòu)造特殊的檢驗(yàn)函數(shù)，并利用逆H?lder不等式，得到了由二階擬線性橢圓型偏微分方程div（A （x，▽u））=div f（x）所描述的系統(tǒng)的雙障礙問(wèn)題的弱解的局部和全局高階可積性.雙障礙問(wèn)題的研究在控制論、優(yōu)化控制、金融問(wèn)題等方面有著廣泛的應(yīng)用.

雙障礙問(wèn)題;局部高階可積性;全局高階可積性;優(yōu)化控制;逆H?lder不等式

設(shè)區(qū)域Ω?Rn有界，是通常的Sobolev空間．設(shè)θ（x）∈e.}．稱(chēng)φ（x），ψ（x）為障礙，θ為邊界值．

考慮區(qū)域Ω上的二階擬線性橢圓型偏微分方程

定義稱(chēng)函數(shù)-雙障礙問(wèn)題（1）的弱解，是指

障礙問(wèn)題出現(xiàn)在非線性位勢(shì)理論、變分極值以及變分不等式理論中［1-2］．它廣泛地應(yīng)用于材料的相變理論、燃燒理論、優(yōu)化控制理論以及金融問(wèn)題中［3-4］．在f（x）=0，A滿(mǎn)足齊次性條件下，文獻(xiàn)［5］得到了（A）-雙障礙問(wèn)題（1）的弱解的高階可積性與穩(wěn)定性結(jié)果．本文討論（A）-雙障礙問(wèn)題（1）的弱解的局部和全局高階可積性．對(duì)單個(gè)障礙的情形，文［6］得到了單障礙問(wèn)題的弱解的高階可積性．

1 主要結(jié)果

設(shè)Ω?Rn是一個(gè)有界區(qū)域，n

n－1＜p＜+∞且s＞p．假設(shè)映射A:Rn×R→Rn是Caratheodory函數(shù)且滿(mǎn)足下列條件:

（A1）存在0＜α＜β＜∞，對(duì)所有h∈Rn以及a.e.x∈Ω，A（x，h）h≥α|h|p，|A（x，h）|≤β|h|p－1;

（A2）對(duì)a.e.x∈Ω和h1≠h2，（A（x，h1）－A（x，h2））（h1－h(huán)2）＞0．

先給出一些記號(hào)．給定x0∈Ω，設(shè)Qr是一個(gè)中心在x0邊長(zhǎng)為r的方體，Qλr（λ＞0）是與Qr中心相同，邊平行且邊長(zhǎng)為λr的方體．記f（x）在Qr中的平均值為

2 主要結(jié)果的證明

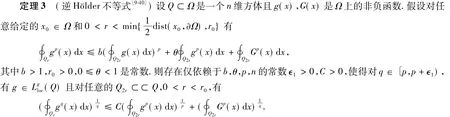
首先，給出一個(gè)定理，其證明請(qǐng)參見(jiàn)Giaquinta和Modica［9］．在上述計(jì)算中，多次使用了H?lder不等式、Young不等式．若取，則由（22）式可得

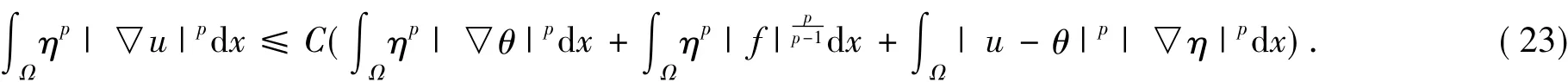
為估計(jì)（23）式中的最后一項(xiàng)，我們利用邊界?Ω是p-Poincaré厚的條件．事實(shí)上，函數(shù)u－θ能連續(xù)零延拓到CΩ，因而

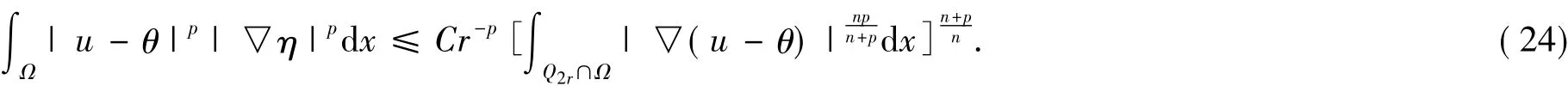
利用Minikowski不等式和H?lder不等式可得

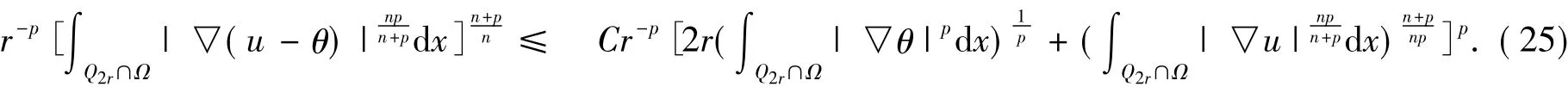
因此由式（23）、（24）和（25）可得

其中C=C（diamΩ，n，p）．

因?yàn)棣取蔐s（Ω），由式（30）可得u∈Lδ（Ω）．記q=min{t，δ}＞p，若p＜n，則u∈W1，q（Ω）．如果p≥n，則上述推理過(guò)程對(duì)任何p*＜∞都成立，再利用Minkowski不等式和H?lder不等式可得u∈Ls（Ω），因而u∈W1，q（Ω）．只要取∈0=q－p，即知定理成立．

［1］HEINONEN J，KILPELAINEN T，MARTIO O.Nonlinear potential theory of degenerate elliptic equations［M］.Oxford:Clarendon Press，1993.

［2］KUBO M，YAMAZAKI N.Periodic solutions of elliptic－parabolic variational inequalities with time－dependent constraints［J］.J Evol Eqns，2006，6（1）:71－93.

［3］BARRON E N，JENSEN R.Minimizing the L∞norm of the gradient with an energy constraint［J］.Comm in PDE，2005，30 （12）:1741－1772.

［4］CAHN J W，HANDWERKER C A，TAYLOR J E.Geometric models of crystal growth［J］.Acta Met，1992，40（7）:1443－1474.

［5］LI G，MARTIO O.Stability and higher integrability of derivatives of solutions in double obstacle problems［J］.J Math Anal Appl，2002，272（1）:19－29.

［6］LI G，MARTIO O.Stability of solutions of varying degenerate elliptic equations［J］.Indiana Math J，1998，47（3）:873－891.

［7］GRANLUND S.An Lp－estimate for the gradient of extremals［J］.Math Scand，1982，50（1）:66－72.

［8］LI G，MARTIO O.Local and global integrability of gradients in obstacle problems［J］.Ann Acad Sci Fenn Ser A I Math，1994，19:25－34.

［9］GIAQUINTA M，MODICA G.Regularity results for some classes of higher order nonlinear elliptic systems［J］.J Fur Reine U Angew Math，1979，311/312:145－169.

［10］IWANIEC T.The Gehring lemma:proceedings of the International Symposium，Ann Arbor，August 1995［C］//P.L.Duren. Quasiconformal mappings and analysis.New York:Springer－Verlag，1998.

［11］GILBARG D，TRUDINGER N S.Elliptic partial equations of second order［M］.2nd ed.New York:Springer－Verlag，1983.

Higer Integrability for Weak Solutions to a Class of Double Obstacle Problems

HU Zhen-hua1，2，ZHOU Shu-qing2*，PENG Dong-yun2
（1.College of Mathematics and Computer Science，Hunan City University，Yiyang 413000，China; 2.College of Mathematics and Computer Science，Hunan Normal University，Changsha 410081，China）

By constructing special test functions and using inverse H?lder′s inequality，local and global higher integrability results to the weak solutions to a class of double problems described by quasilinear elliptic partial differential equations div（A（x，▽u））=div f（x），are obtained.The research of double obstacle can widely be used in control problems，optimal control problems and financial problems.

double obstacle;local higher integrability;global higher integrability;optimal control;inverse H?lder′s inequality

O175.25

A

1000－2537（2011）05－0007－05

2011－03－13

國(guó)家自然科學(xué)基金資助項(xiàng)目（10971061）;湖南省自然科學(xué)基金（11JJ6005）和湖南師范大學(xué)優(yōu)秀青年培養(yǎng)計(jì)劃資助項(xiàng)目（080640）

*通訊作者，E－mail:zhoushuqing87@163.com

（編輯沈小玲）