利用AUTO軟件分析揚聲器薄殼的分岔特性*

李小菊， 張志良

(浙江師范大學數理與信息工程學院，浙江金華 321004)

0 引言

作為音響設備中保真性最薄弱的器件，揚聲器的性能優劣對音質的影響很大．揚聲器的非線性失真分為諧波失真和分諧波失真，人耳對中頻的分諧波失真更為敏感．1935年，Pedersen［1］第一次實驗發現了揚聲器的1/2分諧波，并分析了分諧波產生的2種途徑——參數激勵振動和系統含有平方非線性．Cunningham［2］將揚聲器薄殼振動類比為受軸向簡諧力的彈性直桿的橫向振動，以解釋揚聲器產生分諧波失真的原因．國內，魏榮爵等［3］1986年首次實驗觀測到了揚聲器的分諧波和混沌現象;Zhang Zhilang等［4］實驗觀測到了揚聲器的幅度調制振動和非周期運動，其頻率均在中頻范圍．以上研究沒有采用薄殼模型分析揚聲器非線性現象的產生機制，基本為實驗研究．

本文采用文獻［5］中閉合旋轉薄殼的幾何非線性模態方程，利用分岔分析軟件AUTO［6］分析了揚聲器非線性振動系統處于2∶1內共振情形下的分岔特性，所得分岔集與已有實驗結果基本吻合．

1 非線性方程

假設揚聲器薄殼的幾何參數和材料參數沿周向完全均勻，在小端受到沿周向均勻分布的軸向驅動力．為研究1/2分諧波，選擇受驅動力直接共振激勵的軸對稱模態和1個固有頻率約為軸對稱模態固有頻率一半的非軸對稱模態，即軸對稱模態和非軸對稱模態2∶1內共振．由文獻［5］的結果可寫出這2個模態的非線性振動方程

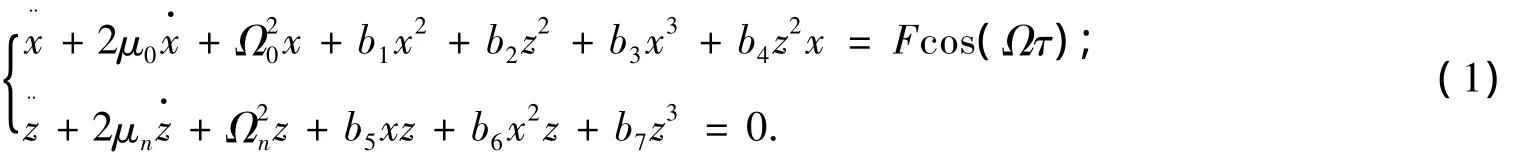
式(1)中:x和z分別表示軸對稱模態和非軸對稱模態的無量綱位移，無量綱因子為揚聲器薄殼厚度;Ω0，Ωn和Ω分別為無量綱的軸對稱模態、非軸對稱模態的固有角頻率和驅動角頻率，無量綱因子為揚聲器的特征頻率ωtb，ωtb可認為是揚聲器作分割振動的起始頻率［7］，其值略小于軸對稱模態的最低固有頻率;無量綱時間τ=ωtbt，故無量綱量組合Ωτ等于有量綱量組合ωt;下標n為非軸對稱模態的周向波數;無量綱驅動力幅F與驅動電壓U成正比，其比例因子設為K．式(1)表明，在周向均勻假設下，僅有軸對稱模態受到驅動力的直接激勵，而非軸對稱模態僅受軸對稱模態的耦合激勵．

為比較本文結果與實驗結果，筆者采用文獻［4］的揚聲器，利用文獻［5］中由有限元法定得的方程(1)的系數進行分析，結果見表1．揚聲器振膜阻尼表現為結構阻尼，考慮到2個模態的振動頻率均在各自的固有頻率附近，取μ0=δΩ0/2，μn=δΩn/2，其中δ為揚聲器紙盆材料阻尼因子，取其標準值為0．04．

表1 方程(1)的系數

本文分析軸對稱模態處于共振激勵，而非軸對稱模態的固有頻率近似為軸對稱模態固有頻率的一半的情形，因此引入如下外失諧因子σ0和內失諧因子σn:

方程(1)的線性解容易求得

由方程(1)中非軸對稱模態的方程可以看出，上述軸對稱模態的線性解對非軸對稱模態相當于參數激勵，且非軸對稱模態在本文研究情形下處于參數激勵主共振情形，因此，可以預計非軸對稱模態將產生1/2分諧波振動．下文采用AUTO軟件分析方程(1)的分岔．

2 分岔特性及穩定性

AUTO軟件是由加拿大康考迪亞大學的Doedel等于1980年開發的分岔分析軟件包，此軟件采用擬弧長延拓算法跟蹤非線性系統的分岔分支，并能判斷解的穩定性，穩定解和非穩定解分別用實線和虛線標出．軟件同時計算系統的弗洛凱乘子，并用不同的符號標注出不同的分岔點．

圖1為2個模態的頻率響應曲線，xm，zm分別為軸對稱模態解和非軸對稱模態解的幅值，實線代表穩定解，虛線代表不穩定解，TR，PD和LP分別代表內衣馬克-沙克分岔點(Neimark-Sacker bifurcation)、倍周期分岔點和切分岔點．曲線上方和下方的箭頭表示解曲線隨頻率增加和減小的路徑，箭頭1，2，3所指頻率處的驅動力響應和時間歷程見下文．圖1中，有共振峰的曲線為軸對稱模態的線性解，零解為非軸對稱模態的線性解．圖1表明:當頻率由低到高增加時，在倍周期分岔點PD1，即σ0=－0．191處，2個模態的線性解變成不穩定解，非線性解變成穩定解，倍周期分岔表明1/2分諧波振動出現，并發生跳變現象;當頻率變化到2個內衣馬克-沙克分岔點之間，即－0．053 4＜σ0＜－0．005 1時，系統不存在穩定解，表明非周期振動出現;然后，經過σ0=0．071處的切分岔點LP2，2模態又跳變到線性解穩定區域．頻率由大減小時，在倍周期分岔點PD2處，即σ0=0．036 9時，兩模態進入非線性解穩定區;而后同樣經歷2個TR分岔點之間的無穩定解區域;當頻率減小到LP1，即σ0=－0．397時，2模態又跳變到線性解穩定區．

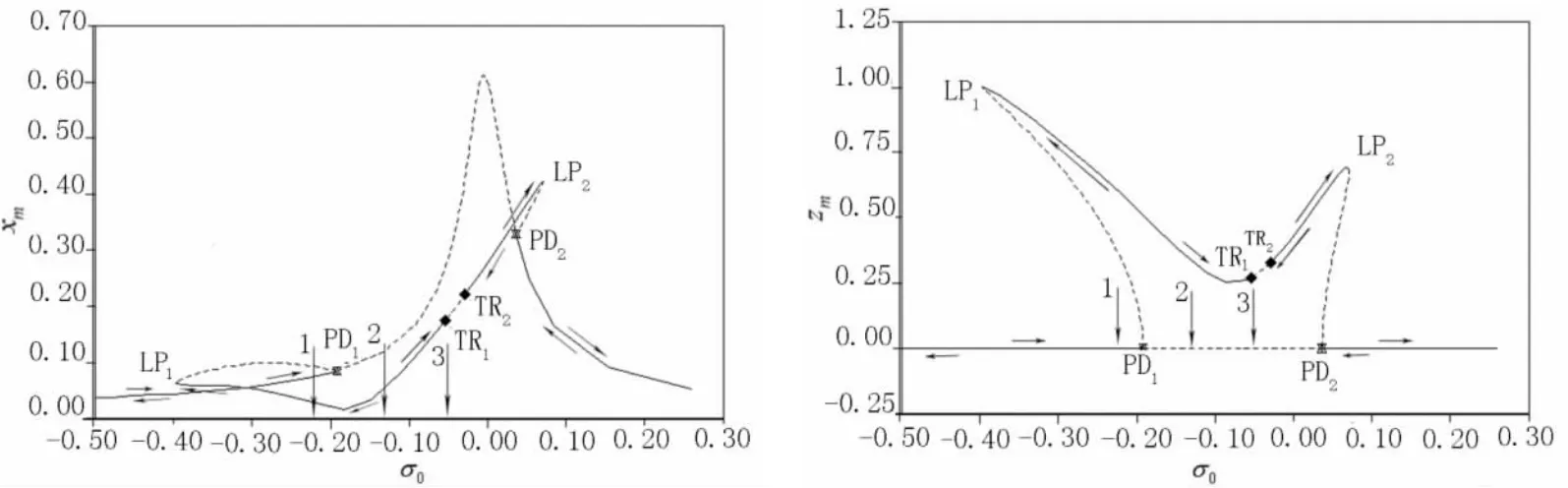
圖1 驅動電壓3 V時的頻率響應曲線

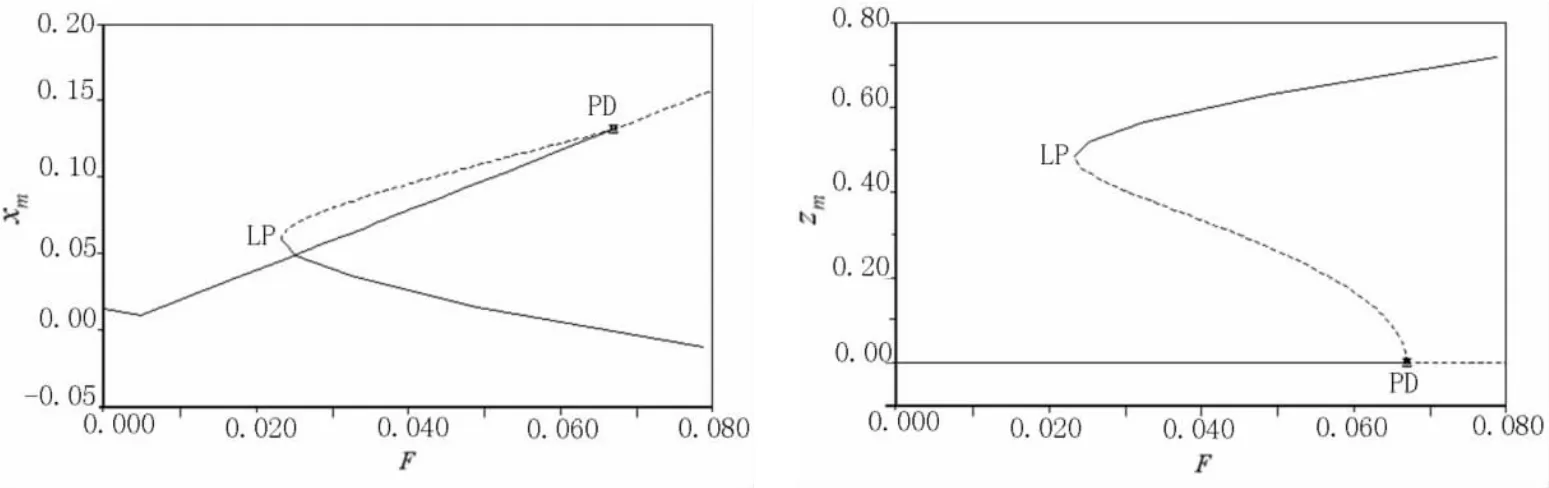
圖2 σ0=－0．22時的驅動力響應曲線

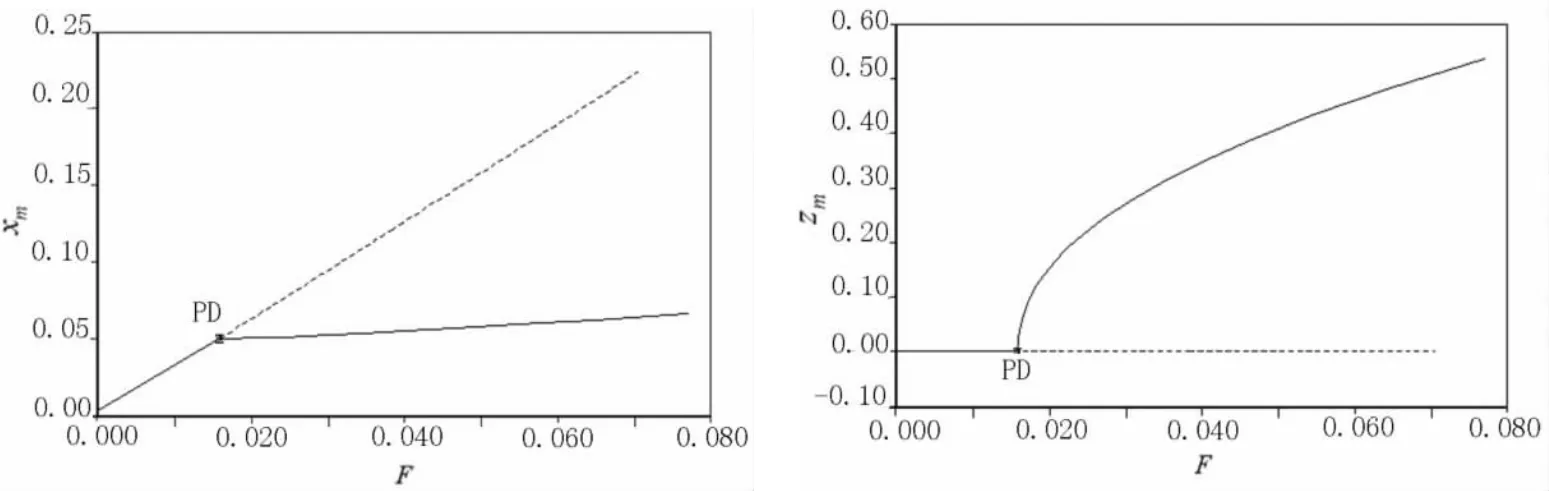
圖3 σ0=－0．13時的驅動力響應曲線

圖1 中，箭頭1，2和3所表示的幾個典型頻率下的驅動力響應見圖2～圖4．同樣，xm，zm分別為軸對稱模態和非軸對稱模態的幅值，實線代表穩定解，虛線代表不穩定解，LP和PD分別為切分岔點和倍周期分岔點．由式(3)可以看出，軸對稱模態線性解的幅值與驅動力成正比關系．因此，圖2～圖4中軸對稱模態解的直線部分對應線性解，非直線部分對應著非線性解;對非軸對稱模態，零解為線性解，非零解對應其非線性解．圖2中，當驅動電壓增大和減小時將分別在分岔點PD和LP點發生跳變現象．圖3中無跳變現象，系統經倍周期分岔點(F=0．023)，進入非線性解穩定區域，此后直接激勵的軸對稱模態的幅值基本不變，出現飽和現象，能量傳遞給了非軸對稱模態，非軸對稱模態的幅值漸漸遠大于軸對稱模態的幅值．圖4中開始情形類似于圖3，但到分岔點TR處后，系統進入無穩定解區作非周期振動．

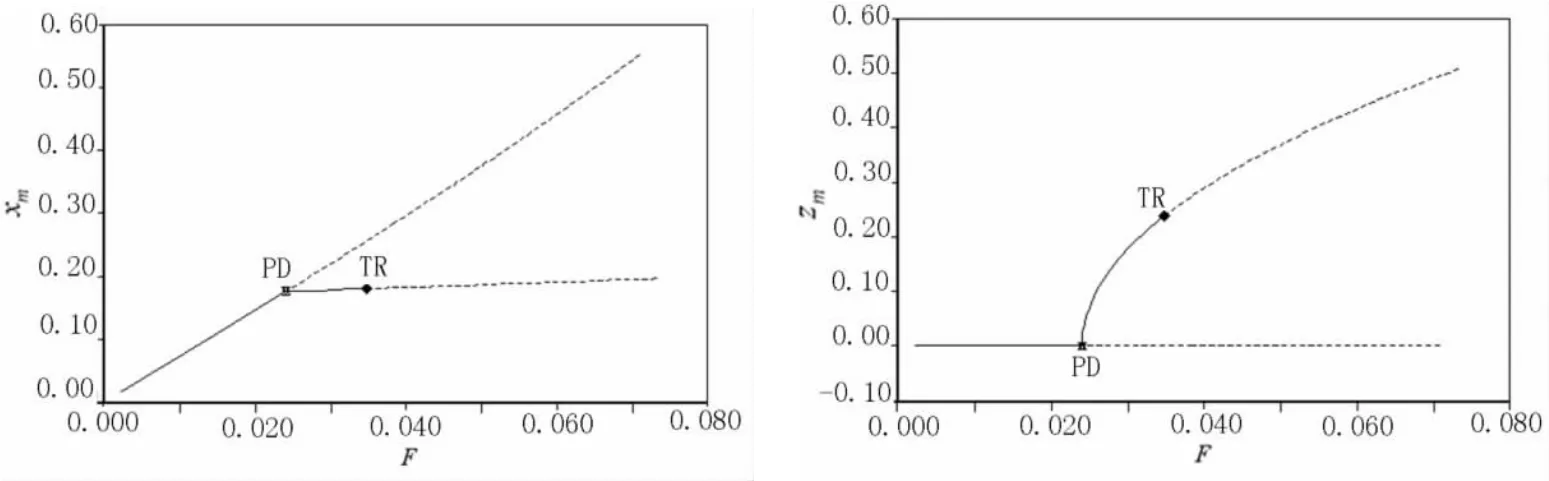
圖4 σ0=－0．05時的驅動力響應曲線

3 時間歷程

對圖1中箭頭1，2和3所表示的頻率下求系統的時間歷程，結果分別示于圖5、圖6和圖7．圖5的頻率位于多值解區，計算中初始值設為零，因此圖中結果為線性解．圖5表明，此時軸對稱模態作穩定的周期振動，非軸對稱模態沒有被激發．圖6為倍周期分岔后2個模態的時間歷程，清楚表明了軸對稱模態和非軸對稱模態的周期成2倍關系，揚聲器出現1/2分諧波．圖7為系統進入TR分岔后的時間歷程，此時振幅隨時間變化，2個模態作幅度調制振動．

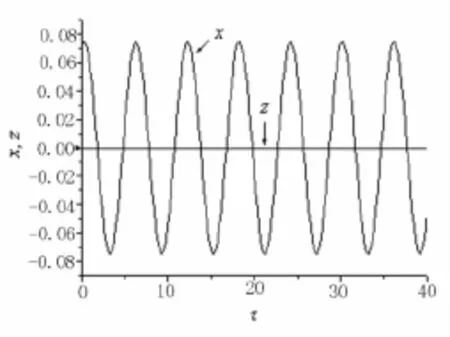
圖5 σ0=－0．22，驅動電壓為3 V時，軸對稱模態和非軸對稱模態的時間歷程

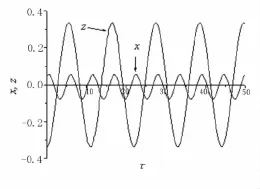
圖6 σ0=－0．13，驅動電壓3 V時，軸對稱模態和非軸對稱模態的時間歷程

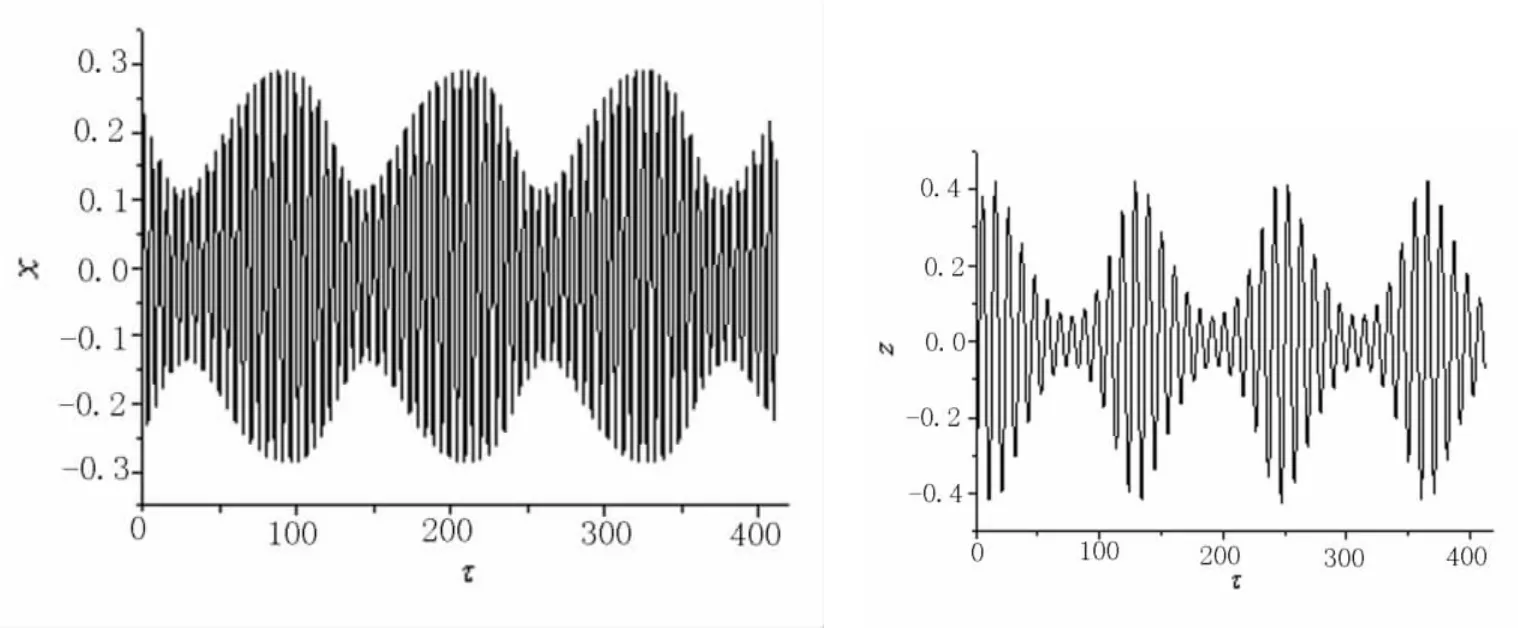
圖7 σ0=－0．05，驅動電壓3 V時，軸對稱模態和非軸對稱模態的時間歷程

4 分岔集和實驗比較

AUTO軟件具有計算分岔集的功能．分別從圖1中的分岔點LP，PD，TR出發計算得到系統σ0-F的平面上的各相應分岔點的分岔集，如圖8中的L1，L2和L3分別為:切分岔集、倍周期分岔集和內衣馬克-沙克分岔集．這3條曲線將σ0-F平面分成3個區域:區域Ⅰ中，線性解不穩定，非線性解穩定且唯一;區域Ⅰ'中含有穩定的線性解、穩定的非線性解和不穩定的非線性解，該區因而為跳變和滯后區;區域Ⅱ中不存在穩定的周期解．文獻［4］中實驗測得結果見圖9，其中Ⅰ區，單值穩定非線性解區;Ⅱ區，無穩定周期解區;Ⅰ'區，多值解區(跳變滯后區)．本文數值模擬結果與其基本吻合，只是實驗中沒有發現明顯的右側跳變滯后區域，在數值分析結果中，此區域也出現了明顯的左右不對稱現象，右側跳變滯后區域明顯小于左側．另外，實驗中發現II區中出現了I區窗口，數值分析中當驅動電壓達到8 V時，II區成為一個閉合的圈，這也和實驗結果相對應，只是此時的電壓已經超出了揚聲器正常工作時的驅動電壓．

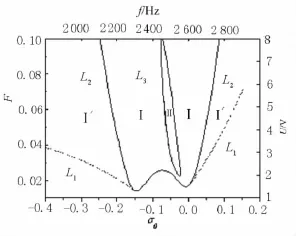
圖8 σ0-F平面的分岔集

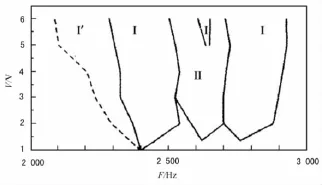
圖9 文獻［4］中實測的解的區域

5 結論

本文結果和已有實驗結果吻合，表明采用的理論模型是正確的，即揚聲器中頻的非線性來自揚聲器薄殼的幾何非線性，揚聲器的分諧波源自軸對稱模態和非軸對稱模態的耦合作用．同時表明分岔分析軟件AUTO是非線性分析的有力工具．

［1］Pedersen P O．Sub harmonics in forced oscillations in dissipative systems part I［J］．Journal of Acoustical Society of American，1935，6(4):227-238．

［2］Cunningham W J．The growth of subharmonic oscillations［J］．Journal of Acoustical Society of American，1951，23(4):418-422．

［3］Wei Rongjue，Tao Qingtian，Ni Wansun．Bifurcation and chaos of direct radiation loudspeaker［J］．Chinese Phys Lett，1986，3(10):469-472．

［4］Zhang Zhiliang，Tao Qingtian．Experimental study of non-linear vibrations in a loudspeaker cone［J］．J Sound and Vibration，2001，248(1):1-8．

［5］孟慶照，李小菊，張志良．閉合旋轉薄殼的非線性模態方程［J］．浙江師范大學學報:自然科學版，2010，33(1):63-69．

［6］Doedel E J，Champneys A R，Dercole F，et al．Auto-07P:Continuation and Bifurcation Software for Ordinary Differential Equations(with Homcont)，User'Guide［EB/OL］．［2008-11-20］．http://indy．cs．concordia．ca/auto．

［7］張志良．揚聲器錐殼的全頻段振動通解［J］．聲學學報，2010，35(5):554-561．