光聲耦合方程組的近似解*
李華星, 林 機
(浙江師范大學數理與信息工程學院,浙江金華 321004)
0 引言
光波在布拉格光柵中傳播時,因其具有較大的群速度色散和非線性效應而可以形成孤立子.Eggleton等[1]和Taverner等[2]分別在實驗中發現了布拉格孤子和帶隙孤子,其中后者是布拉格孤子頻譜在光子帶隙內時的特殊情況;而在理論上,文獻[3]首先提出了帶隙孤子的概念;de-Sterke等[4]給出了光波在布拉格光柵中傳播所遵循的耦合方程組,給出了相應的帶隙孤子解,并分析了其性質.目前,布拉格光柵中帶隙孤子的傳播和穩定性也受到人們的廣泛關注[5-6].此外,由于布拉格光柵的色散效應,帶隙孤子的速度可以遠小于光速,在此基礎上,學者們[7-9]深入分析了帶隙孤子抑制光速的原因.
近幾年來,光聲相互作用引起人們廣泛的關注[10-12].考慮電致伸縮的情況下[13-16],在布拉格光柵中光波帶隙孤子可以與聲波耦合,從而形成一種新的帶隙孤子——光聲孤立子.光聲孤立子的概念最早是由Tasgal等[17]提出的,并給出了光波和聲波在布拉格光柵中傳播所遵循的耦合方程組,在電致伸縮對介質密度的影響下,發現孤子的速度可以減小到接近聲速.可見,光聲孤立子也可以抑制光傳播的速度.然而,Tasgal等只是在特殊情況下給出了單光聲孤立子解析解,并且用數值方法給出了孤子的裂變圖像,并沒有給出更多的解析解.目前對此方程的解析解研究也很少,原因是方程不可積,一般的孤子理論方法難以運用此方程,尋找一般情況解是很困難的.文獻[18]運用多重尺度方法分析了玻色-愛因斯坦凝聚中的暗孤子解及其碰撞,這種方法思路簡單,過程簡潔,而且把復雜的耦合方程組轉化成已經有解或容易求解的簡單方程.因此,本文運用多重尺度方法簡化在布拉格光柵中的光聲耦合方程組,并得到了方程的近似解,如單孤子解、二孤子解,并分析了解的性質.
1 多重尺度約化和非線性薛定諤方程
在布拉格光柵中,光聲耦合方程組有如下形式:
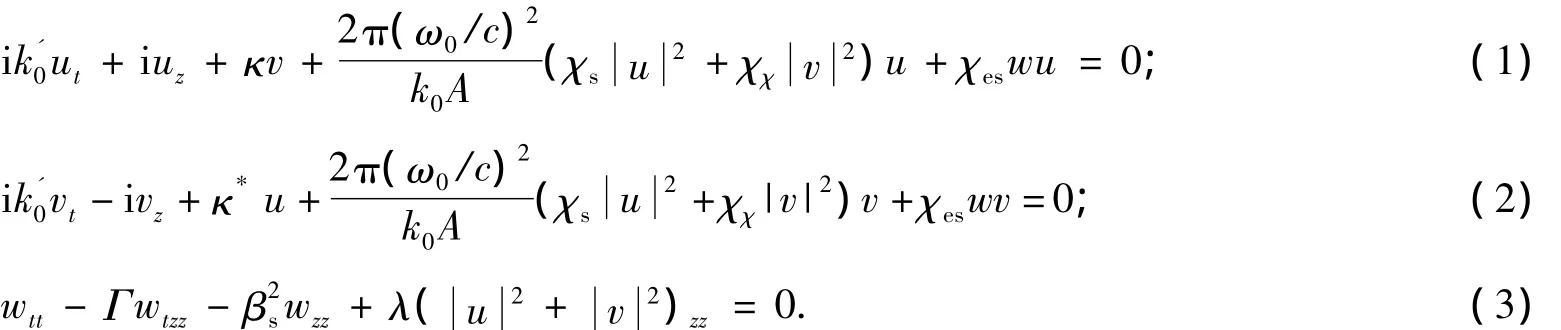
其中:下標表示對時間變量t和空間變量z的求導;k'0=dk/dω(ω=ω0)表示光波的群速度;κ是布拉格反射率;κ*是κ的復共軛;c代表光速;i表示虛數單位;χχ和χs分別表示交叉相位調制和自相位調制系數;A代表波導的有效區域;λ和χes分別表示由能量密度和波矢變化引起的電致伸縮系數;βs是聲速;Γ為聲波的粘滯系數;u=u(z,t)和v=v(z,t)表示反向傳輸的光波包絡函數,w=w(z,t)表示聲波區域介質的密度波動.
首先,運用多重尺度方法對方程組的光場量和聲場量漸近展開為:

其中:u(j),v(j),w(j)是多尺度變量(z,t,ξ= ε(z-cst),τ =ε2t)的函數;ε 為無窮小參量.然后,把這些未知函數代入方程式(1)~式(3),令各階ε的系數為零,在第1階(j=1)時,可得到:

由式(7)和式(8)可以給出:

和線性色散關系

式(10)~式(12)中:F是多尺度變量ξ=ε(z-cst);τ=ε2t的函數;k和ω分別表示光波的波數和載波的中心頻率.并且式(10)、式(11)滿足式(9).在第2階(j=2),有:

由此可以給出:

其代表波包的群速度.而且u(j)和v(j)(j=1,2)滿足方程(15).在第3階(j=3),可給出:

由式(19)、式(20)得出:

式(23)中:B,C,D,F是與方程(1)~(3)中參數有關的常數.

然后,由u(j),v(j)和式(21)可以得到
因此,式(23)可以化簡為
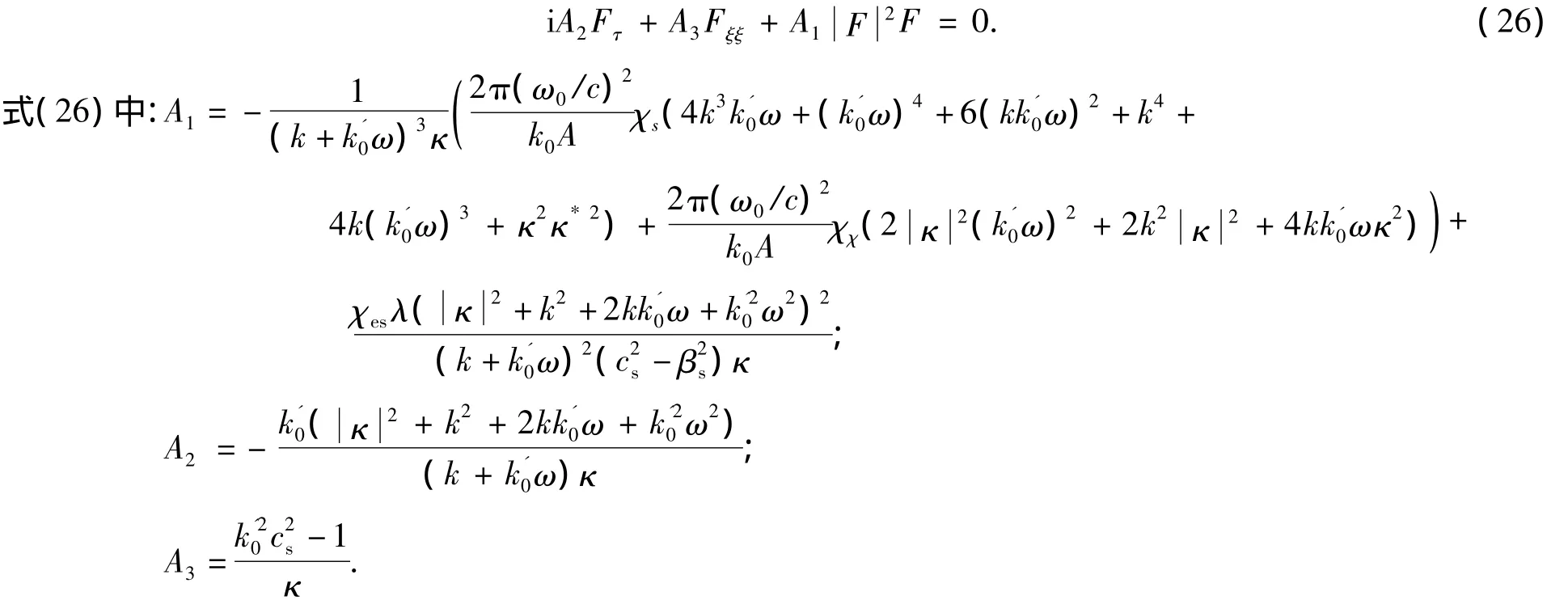
然后,作變換把式(26)還原成關于z,t的方程,設G=εF和作變換
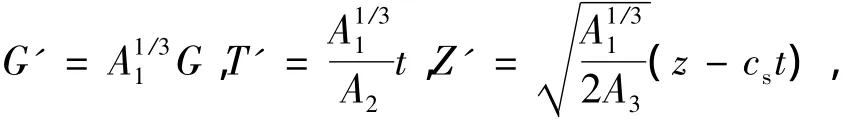
由ξ和τ的定義,式(26)可化為

這就是標準的非線性薛定諤方程,是一個完全可積方程,因此,可以通過這樣的近似簡化,給出光聲耦合方程組的近似解.
2 孤子解
式(27)的單孤子解為[19]

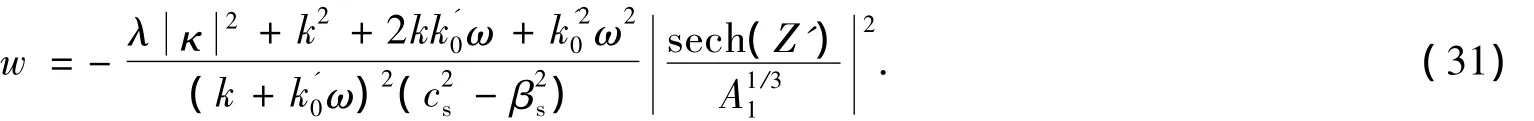
孤子解由如下參數表征:cs代表孤子的速度;A1決定孤子的寬度和振幅;A3與孤子的寬度有關.而且,上文給出了A1和A3的具體表達式.對于單孤子解的圖像,演化比較簡單,這里不予給出.當βs=0.2,且有以下參數取值時:k=0.25,k'0=κ=1,由式(18)得到光孤子的速度cs=0.27,容易看出光波的速度與聲速很接近,可見光聲孤立子的相互作用可以產生抑制光速的效果.
同樣地,可得出光聲耦合方程組的二孤子碰撞的解[20]為:

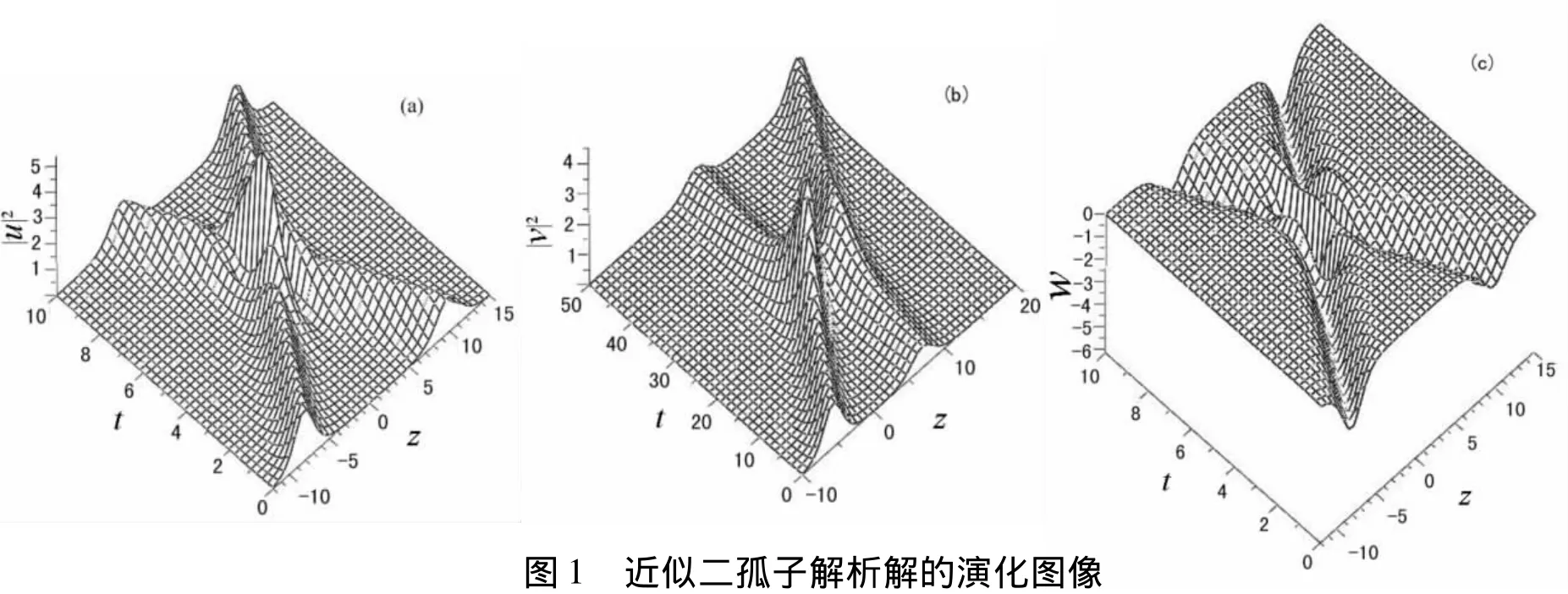
其中:
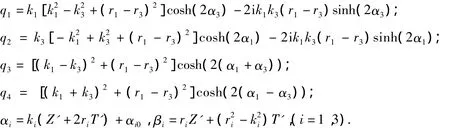
圖1給出了光聲耦合方程組的二孤子碰撞的圖像,具體參數取值如下:

可以看出,二孤子穩定地傳播,碰撞后其形狀和速度不發生變化.
3 結論
運用多重尺度方法研究了光聲耦合方程組,將其約化為標準的非線性薛定諤方程.利用非線性薛定諤方程的解,得到了原方程組的單孤子解、二孤子解,并且借助計算機描述了孤子解的圖像.根據孤子速度的表達式,看到光聲孤立子也可以抑制光傳播的速度.人們普遍認為,由于在頻率等參數上有很大差別,光聲相互作用是非常微弱的,然而,由以上分析可以清楚地看到光波和聲波的相互作用.但是,如果想更深入地理解光聲作用的內在機制,必須更好地理解電致伸縮效應所起的作用.
[1]Eggletn B J,Slusher R E,Sterke C M.Bragg Grating Solitons[J].Phys Rev Lett,1996,76:1627-1630.
[2]Taverner D,Broderick N G R,Richardson D J.Nonlinear self-switching and multiple gap-soliton formation in a fiber Bragg grating[J].Opt Lett,1998,23(5):328-330.
[3]Chen Wei,Mills D L.Gap soliton and the nonlinear optical response of superlattices[J].Phys Rev Lett,1987,58(2):160-163.
[4]de-Sterke C M,Sipe J E.Gap Solitons[M].Amsterdam:Elsevier,1994:203.
[5]Kazantseva E V,Maimistov E V.Polaritonic gap-soliton propagation through a wide defect in a resonantly absorbing Bragg grating[J].Phys Rev A,2009,79(3):033812.
[6]Kalithasan B,Porsezian K,Senthilnathan K,et al.Generation of self-induced-transparency gap solitons by modulational instability in uniformly doped fiber Bragg gratings[J].Phys Rev A,2010,81(5):053802.
[7]Winful H G,Raman V P.Gap solitons[J].Phys Rev Lett,2000,84(16):3586-3589.
[8]William C K M,Malomed B A,Chu P L.Formation of a standing-light pulse through collision of gap solitons[J].Phys Rev E,2003,68(2):026609.
[9]Mok J T,Sterke C M,Littler I C M,et al.Dispersionless slow light using gap solitons[J].Nature Phys,2006(2):775-780.
[10]Zhao C,Ju L,Fan Y,et al.Observation of three-mode parametric interactions in long optical cavities[J].Phys Rev A,2008,78(2):023807.
[11]Fermann M E,Silva V D,Smith D A,et al.Shaping of ultrashort optical pulses by using an integrated acousto-optic tunable filter[J].Opt Lett,1993,18(18):1505-1507.
[12]Verluise F,Laude V.Amplitude and phase control of ultrashort pulses by use of an acousto-optic programmable dispersive filter:pulse compression and shaping[J].Opt Lett,2000,25(8):575-577.
[13]Buckland E,Boyd R W.Measurement of the frequency response of the electrostrictive nonlinearity in optical fibers[J].Opt Lett,1997,22(10):676-678.
[14]Buckland E,Boyd R W.Electrostrictive contribution to the intensity-dependent refractive index of optical fibers[J].Opt Lett,1996,21(15):1117-1119.
[15]Agrawal G P.Nonlinear Fiber Optics[M].賈東方,余震虹,談斌,等,譯.北京:電子工業出版社,2002:32.
[16]Hardman P J,Townsend P D,Poustie A J,et al.Experimental investigation of resonant enhancement of the acoustic interaction of optical pulses in an optical fiber[J].Opt Lett,1996,21(6):393-395.
[17]Tasgal R S,Band Y B.Optoacoustic solitons in Bragg gratings[J].Phys Rev Lett,1998(24):243902.
[18]Huang Guoxiang,Velarde M G.Dark solitons and their head-on collisions in Bose-Einstein condensates[J].Phys Rev A,2001,64:013617.
[19]He Xugang,Zhao Dun,Li Lin,et al.Engineering integrable nonautonomous nonlinear Schr?dinger equations[J].Phys Rev E,2009,79:056610.
[20]Li Huamei,Li Yishen,Lin Ji.Abundant exact solutions for a strong dispersion-managed system equation[J].Chin Phys B,2009,18:3657.

