量子密碼及BB84協議的分析

翟晨曦 鄭心如 楊建偉

(東南大學吳健雄學院610081班,江蘇南京 211189)

量子密碼及BB84協議的分析

翟晨曦 鄭心如 楊建偉

(東南大學吳健雄學院610081班,江蘇南京 211189)

擁有強大破密功能的量子計算機的出現預示著傳統的RSA密碼算法最終將被淘汰.要對付量子計算機驚人的密碼破譯功能,唯一途徑就是運用量子密碼技術.作為量子密碼術中最基本的協議,BB84協議有其獨特的優勢.盡管我們是一年級學生,但在《雙語物理導論》課程教育理念的鼓勵下,帶著對量子密碼的興趣,我們小組展開了對它的初步研究,闡述了量子密碼學原理及BB84協議,并就此分析了其安全性及制約因素.

量子密碼原理;BB84協議;安全性;制約因素

1 量子密碼學原理

微觀世界的粒子有許多共軛量,如位置和速度、時間和能量,都是一對共軛量,在某一時刻,人們只能對一對共軛量之一進行測量,不能同時測得另一個與之共軛的量,比如對位置進行測量的同時,就失去了對速度進行測量的可能性.

海森堡量子測不準原理:對于任意兩個量子的測量值 A和B,有

式中 ,ΔA=A-〈A〉,ΔB=B-〈B〉,[A,B]=AB-BA.

可見,(ΔA)2和(ΔB)2反映了測量值 A和B的不確定性.由于測量值存在不兼容性,即對于[A,B]≠0,測量值 A的不確定性(ΔA)2的減少將迫使測量值B的不確定性(ΔB)2增加,反之亦然,因此不可能同時準確測量A和B,對其中一個的測量將影響對另一個的測量.

在傳統的物理信道中,當存在竊聽者時,收發雙方不會知道竊聽者的存在,尤其像光盤或無線電波,其中所攜帶的信息在被復制或截收時都難以被發現.但當信息以量子為載體時,根據量子力學的原理,微觀世界的粒子的位置不可能被確定,它總是以不同的概率存在于不同的地方.對未知狀態的量子系統的每一次測量都必將改變系統原來的狀態.反過來說,如果系統狀態沒有改變,也就沒有測量或竊聽行為的發生.也就是說,一個位置的量子狀態不可能被復制或克隆,因此它也被稱為不可克隆原理.量子密碼學利用了量子的不確定性,一旦信道上有竊聽發生,通信本身必然受到影響,從而達到發現竊聽者的目的,保證信道的安全.

但這個密碼系統的缺點是通信者只能在機密消息傳送之后才能發現是否有竊聽的出現,而不能在過程中察覺.因此通常在使用信道傳輸真正的機密消息之前,只用量子密碼方法傳輸一個隨機的密鑰,來判斷該信道是否安全.實際上這是為了保證通信安全的一個基本處理原則.隨機密鑰可以是一個隨機的比特序列.這樣,當消息正在傳輸時,竊聽者通過測量量子系統的狀態來讀取消息時必然改變原有狀態.如果通信雙方發現密鑰在傳輸過程中已受到竊聽,他們就丟棄它.然后他們重新傳輸另一個隨機密鑰,直到沒有竊聽出現為止.

2 BB84量子密碼協議

BB84量子密碼協議是第一個量子密碼通信協議,由Bennett和Brassard于 1984年創立.它基于兩種共軛基的四態方案,用到了單光子量子信道中的測不準原理.BB84也是唯一被商業化實現的量子密鑰分發協議.

BB84密鑰分發協議用光子作為量子系統.光子有一個固有的稱為極化的屬性,一個光子或者被+基極化,或者被×基極化.假設通過一個垂直極化的濾光器發送一串光子流,則它們被垂直極化至“|”方向上.之后通過另一個極化濾光器來測量,這個用于測量的濾光器可以改變它與垂直方向的角度,只有當測量濾光器位于水平位置“—”方向時沒有光子能通過它,其余角度均有光子通過.實際上,每一個光子都以一個確定的概率穿過這個測量濾光器,這個概率連續地從100%(濾光器處于垂直位置時)變化到50%(濾光器處于45°時)再變化到0%(濾光器處于水平位置時).

2.1 無噪聲BB84量子密碼協議

我們用單光子的極化狀態來描述BB84協議,這里選擇×基或+基極化編碼方案(和|表示bet1,/和—表示bet0).Bennett和Brassard指出,如果Alice只用一種特定的極化編碼方案與Bob進行通信,則 Eve的竊聽可能不會被發現.因為Eve能100%準確地截取到Alice傳輸的內容,然后假裝Alice重傳她收到的內容給Bob,Eve所用的這種策略稱為不透明竊聽.

為了確保能夠發現Eve的竊聽行為,Alice和Bob需要進行兩階段的通信.

在第一個階段,Alice通過量子信道單方向每次傳輸單個比特,每個比特對應光子的一個極化狀態,她等概率地使用×基極化或+基極化兩種方式.Bob只要將測量儀的極化方式設置得與發送方一致,接收正確率就是100%,否則正確接收的概率是50%.由于×基極化和+基極化的測量儀不能同時使用,對Alice所傳送的每一位,Bob可以選擇+基極化或×基極化進行測量,有50%的概率猜測正確.因此總體上Bob正確接收Alice傳輸的比特的概率是

對于由Alice傳輸的每一比特,假定Eve竊聽的概率為λ(0≤λ≤1),則不竊聽的概率為1-λ.由于Bob和 Eve都是相互獨立地設置測量的位置,也與Alice的設置沒有聯系,Eve的竊聽將對Bob接收的結果產生影響,這種影響是可發現的.由于Eve的竊聽使得Bob的錯誤接收率從25%變到

這樣如果 Eve對每一位都竊聽,即λ=1,則Bob接收出錯的概率從25%增加到37.5%.

在第二階段,Alice和Bob通過公共信道進行通信公開比對自己濾光器的基矢設置,再通過分析Bob的接收出錯率來檢查是否遭到竊聽.

首先Alice和Bob要去除錯誤的比特.他們通過比較濾光器的基矢設置留下相同的比特部分,對于其他濾光器基矢設置不正確的比特則扔掉.這樣他們分別得到各自的原密鑰.如果沒有入侵行為發生,則Alice和Bob的原密鑰將是一致的.如果 Eve實施了竊聽行為,則Alice和Bob的原密鑰不一致的概率是

之后Alice和Bob通過公共信道啟動一個雙向會話來判斷是否遭到竊聽.在沒有噪聲的環境中,Alice和Bob的原密鑰只要有不同就說明有入侵.因此要發現 Eve的入侵,Alice和Bob從原密鑰中隨機選擇一個比特數為m的子序列進行公開比較.如果完全一致,Eve竊聽但不被發現的概率是

如果 Pfalse足夠小,Alice和Bob可認為沒有竊聽出現,可將余下的原密鑰作為他們最終通信的秘密密鑰.如果取λ=1且 m=200,則

這個概率小到可以忽略.

2.2 有噪聲BB84量子密碼協議

實際的通信環境通常是有噪聲的.這時候Alice和Bob就不能區分傳輸發生的錯誤是由噪聲引起的還是由 Eve的竊聽引起的.為了安全起見,他們必須假設所有錯誤都是由 Eve的竊聽引起的.

和無噪聲情形一樣,整個協議工作分為兩個階段.第一階段是基于量子信道的通信,除了錯誤可能由噪聲引起外,其他和無噪聲情況完全一致.

第二階段Alice和Bob基于公共信道進行四個通信過程.

確定原密鑰這個過程除了Alice和Bob刪除那些Bob已經收到但并未接受的比特外,其余與無噪聲情況完全一致,這里所說的未接受比特可能是由Eve的入侵或Bob的探測器的噪聲引起的,后者稱為“暗計數”,發生的位置由Bob通過公共信道告訴Alice.

原密鑰錯誤估計Alice和Bob通過公共信道來估計原密鑰中的出錯率.他們公開地選定原密鑰的一個隨機取樣并比較這些位以獲得錯誤率的估計值 R.這些位將被從原密鑰中刪除.如果 R超過了一個極限值Rmax,那么Alice和Bob不可能獲得最終的共享密鑰,Alice和Bob只能回到第一階段重新開始.

確定協調密鑰這一步的目的是要從原密鑰中清除所有的錯誤比特以產生一個無錯誤的密鑰,稱為協調密鑰.首先,Alice和Bob協商一個隨機的置換規則作用于他們各自的原密鑰.接下來,Alice和Bob將原密鑰分成長度為1的分組,這里選擇長度1是為了保證該長度的分組不可能包含超過一位的錯誤.對于每一個這樣的分組,Alice和Bob公開地比較整個分組的偶校驗,每次要將被比較分組的最后一位丟棄.如果偶校驗比較出現不一致,Alice和Bob就將這一組再分成兩個子分組,對這兩個子分組的每一個進行偶校驗,丟棄每一個子分組的最后一位.這種操作稱為雙叉誤差搜索.重復進行這一操作直到所有的錯誤比特被發現和刪除,再繼續處理下一個分組.

Alice和Bob隨后公開地隨機選取剩余原密鑰的子集,公開地比較偶校驗結果,每次處理所選定的密鑰取樣中的一位.如果一個偶校驗不一致,就用雙叉誤差搜索來確定和刪除錯誤位.

確定最終密鑰Alice和Bob現在已有一個協調密鑰,這個密鑰對Eve只是部分保密的.他們要確定的最終密鑰,就是從這個部分保密的密鑰中抽取出來的秘密密鑰.

設在誤差估計為 R的情況下,Alice和Bob獲取了一個n位的協調密鑰,該密鑰被 Eve知道的位數的上限為k.他們隨后選擇協調密鑰的n-k-s位的子集,s是一個理想的安全參數,可由 Alice和Bob調整.他們不公布其內容及奇偶校驗結果.這個保密的內容成了共享的最終密鑰.可以證明Eve關于最終密鑰的平均信息低于2-s/ln2位.

2.3 BB84量子密碼協議實例演示

續表

3 量子密碼分析

3.1 量子密碼的安全性分析

量子密碼的安全性分析是指被竊聽但沒有發現的概率.A傳送一個比特,B正確接收的平均概率為3/4,因此,如果A發送 N比特,則B平均可得到3N/4個正確的比特,減去B公布的 x%用于檢驗的比特,實際A、B間可作為密鑰共享的比特只有:3N/4(1-x%).之前說過,沒有竊聽時,A驗證的所有比特都是正確的.當A驗證的比特中出現錯誤時,說明一定有竊聽的出現.但當A驗證的所有比特都沒有出現錯誤時,遭到竊聽但沒有發現的概率是多少呢?按照剛才的假設,如果B公布 x%的比特,則B需要公布3N/4×x%比特用于驗證,因為每個比特被竊聽而不被發現的概率為1-λ/4,而共公布的比特數為3N/4×x%,因此這些公布的比特被竊聽而不被發現的概率為

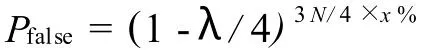
也就是說,C竊聽的概率λ越高,即竊聽的位數越多,A、B間發送的比特數 N越多,B公布的比特比例 x%越大,則竊聽不被發現的概率 Pfalse就越小.

一般來說B公布的比特比例為1/3,即 x%=1/3,如果A、B間發送的比特數為 N,則在無竊聽的情況下,A、B間所發送的比特能用作密鑰共享的比特數為:3N/4(1-x%)=3N/4(1-1/3)=N/2,即實際可作為密鑰共享的比特數只占發送比特的1/2,因此,如果需要得到典型的128位的密鑰,則平均至少要求 N=2×128=256比特,考慮到在極端情況,即 Eve對每一位都進行竊聽,此時λ=1,則竊聽不被發現的概率為

由此可見,當選取的位數足夠多時,C進行竊聽而不被發現的概率幾乎為零.所以量子密碼可以抵抗擁有無窮計算能力的攻擊者,這一點要大大優于現有的其他密碼算法.隨著計算機計算能力的不斷增強,認為量子密碼學是未來唯一安全的密碼技術也未嘗不可.

3.2 量子密碼面臨的制約因素

目前,阻礙量子密碼術走向實用還存在一些技術問題:

首先,由于光纖具有損耗低、穩定性高以及能實現長距離傳輸的優點,所以可以考慮在光纖中建立量子信道,信息載體采用單光子.但問題是制造出高效地單光子源比較困難,這是因為在實際中獲得理想的單光子很困難.而另一個關鍵問題是我們還需要有能在所需波長條件下工作的高效地單光子探測器.

我們還要防止竊聽者假扮合法通信者非法獲取通信信息.因此量子密碼要走向實用必須結合一些經典技術,如保密加強、糾錯及認證技術等.這在一定程度上也減弱了量子密碼術在技術上的優勢.

量子密碼系統即使沒有竊聽者竊聽,由于系統自身的不穩定性也會造成一定的長期誤碼率,使通信的質量受到影響.事實上在實際量子通信系統傳輸過程中,光探測器暗計數誤碼、信道噪聲所產生的誤碼也會導致一定的誤碼率.

阻礙量子密碼術走向實用很重要的非技術問題則是經濟問題.因為量子通信技術必須與傳統的通信技術來競爭以獲得市場,而這些傳統方法在長距離傳輸上以及成本費用上的優勢使量子密碼通信技術處于不利地位.

4 發展前景

量子密碼從理論設想到現在已實現的在常規光纜線路上傳輸達幾十千米的量子密碼系統只用了短短幾年的時間.如此迅速之發展足以證明量子密碼技術的強大生命力.它的前途是不可估量的.在不久的將來,隨著單光子探測等技術的不斷發展,量子密碼技術在全光網絡和衛星通信等領域的應用潛力會不斷成熟.量子密碼已是密碼學領域的一個新的成員,而且必將成為光通信網絡中數據保護的有力工具.在將來要對付擁有量子計算能力的密碼破譯者,量子密碼可能是唯一的選擇.

[1] 陸果.基礎物理學教程[M].北京:高等教育出版社,2008.494～497

[2] 曾貴華.量子密碼學[M].北京:科學出版社,2006.256～270

[3] 馬瑞霖.量子密碼通信[M].北京:科學出版社,2006.42～44,56～57

[4] 胡向東,魏琴芳.應用密碼學[M].北京:電子工業出版社,2006.318～325

2010-04-06;

2010-09-21)