熵增意味著能量的貶值

韓 鋒

(河池學院 物理與電子工程系，廣西 宜州 546300)

熵增意味著能量的貶值

韓 鋒

(河池學院 物理與電子工程系，廣西 宜州 546300)

從熱力學與統計物理學的觀點說明:系統熵的增大就意味著能量可利用程度的減小，或者說伴隨著熵增的是能量的貶值。

熱力學與統計物理學;熵增;玻爾茲曼關系;可利用能;能量的貶值

從物理學中生發出來的“能量”這個概念，使人們感到既重要又困惑。說它重要，是因為它是這個世界的四大基本要素——物質、運動、空間、時間之一。愛因斯坦的引力場方程將這四者聯系在一個方程式中，而被認為是至今物理學理論的最高成就。在社會生產和生活中把耗能降下來，以及使能量重復使用，發展循環經濟，也一直是一個重要課題。

說它令人感到困惑，是因為它作為一個物理量，表現形式多種多樣，僅就機械運動度量中的動能和動量之爭，就使許多物理學家和哲學家們傷透了腦筋。尤其是，在近現代物理學中，力的概念正在逐漸退出歷史舞臺，而被更方便和更普遍的能量概念所取代［1］，就更顯示出能量這一概念的不同尋常。

一般認為，把能量定義為作功的能力或本領，還是比較確切的。因為功在物理學中有明確的定義，因而能量也就獲得了較為明確的含義。說能量是物質運動的量度當然不錯，但把它作為一個物理哲學的定義合適，作為一個物理量的定義則嫌其缺乏操作性。

物質所含的能量既有可作功的部分(這是主要的)，也有不可作功的部分(這是次要的)，但也同樣值得我們關注。

1 從能量守恒到能量貶值

在一切自然過程中，能量的形式盡管可以互相轉化，但它的總量卻總是守恒的，這是一個對過程的很強的限制。由于其普遍性而成為今日科學理解的出發點，而被稱為“自然界的憲法”。

隨著系統熵的增大，能量可利用的程度在逐漸降低，能量的品質在逐漸退化，能量越來越多地不能被用來作功了。學術界把這種能量價值的降低稱為“能量的退降”［4］。這一點非常重要，但卻往往沒有引起人們更多的注意。在不可遞的體系演化過程中，可用的能量總是越來越少，而其相反的量(克勞修斯稱之為熵)則總是越來越大，它最后總是要傾向于達到一個最大值，那就是平衡態。當系統處于平衡態時，系統中各部分的溫度、壓強、密度均勻分布，系統表現出很高的對稱性(均勻性、各向同性)，沒有明顯的集中定向的運動，即系統的無序度(混亂度)最大。這樣的系統，就失去了集中定向作功的本領。總之，一個孤立的物質體系，系統會自發地、不可逆地趨向熵極大的平衡態，除非外界輸入負熵(可以是物質或者能量)，以壓低系統走向平衡態的速度，但這個總的趨勢是不會改變的。對于近平衡的開放系統，由于約束(例如溫度差)，系統不可能達到平衡態，但它可以盡可能地接近平衡態。一旦連續改變外界條件，減小以至消除約束時，系統就又會從非平衡態連續地向平衡態過渡。只有在遠離平衡態的非線性區域，系統才會出現自組織，出現新的穩定的、相對有序的結構。

1.1 在熱力學意義上，熵是不可用能的量度

在熱力學中，熵的增大并不直接表現為能量的貶值。那么，如果說熵是不可用能量的量度，能量的貶值又是如何用熵增原理來描述的呢［5］?

假設有一個盛有質量M，自由度為i的理想氣體的絕熱容器，在它與環境之間裝有一臺卡諾熱機。這時容器就是一個可變溫度的高溫熱源，環境是一個溫度為T0的低溫熱源。當容器中的溫度由T逐漸降低到環境溫度T0時，卡諾熱機作功為:

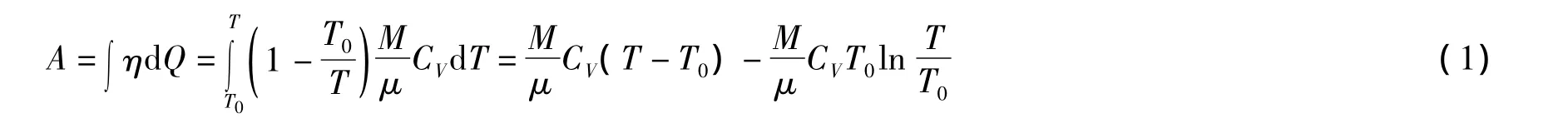
這就是系統在末態所具有的可以轉化為機械能的那部分能量，可以稱之為內能中所含有的可用能。在卡諾熱機中一部分內能轉化為機械能的同時，必有另一部分內能以熱量的形式釋放到環境中去。因為熱機的效率不可能是100%，所以這種耗散是必然的。這部分能量為:

這是末態中不能轉化為機械能的部分，可以稱之為末態內能中的不可用能。

在此過程中，系統熵的增量為:

由此式參照式(2)可知，對于與溫度為T0的環境相接觸的系統，不可用能就是:

由此可見，對于一定環境溫度T0的系統，不可用能與熵的增加成正比。這就是說，熵增可以理解為不可用能的一種量度(確切的說，是能量退化或退降為不可用能的一種量度)［6］。所以，也可把這作為熵的一種宏觀定義。由于熵是系統無序度的一種量度，所以隨著系統無序度的增大，不可用能亦隨之增大。如果把不可能再作功的這部分能量理解為整個內能中的一種“無序”能量，那么熵的增加就意味著能量的可利用度下降，意味著能量的貶值。

某規模化豬場長白、大白和長大二元豬的繁殖性能比較分析…………………………………蘇晶晶，陳德福，隋世燕（75）

1.2 在統計物理學意義上，不可用能的量度

按照熱力學第二定律的統計解釋，一切孤立系統都將由熱力學幾率較小的狀態向熱力學幾率較大的狀態過渡，這一過程將伴隨著系統熵的恒增。這個關系由著名的玻爾茲曼關系式表述。

由于在平衡態系統的熱力學幾率最大，但這時系統的熵也最大，可見系統的熵S與熱力學幾率W之間必定有著某種密切相依的正相關關系，我們把這種正相關的函數關系記作S∝f(W)，或者就記作:這里的常數k就是我們現在所說的玻爾茲曼常數。

考慮把一個系統分成獨立的(或相互作用微弱的)兩個部分1和2，根據熵這種廣延量的可加性［7］，系統的總熵 S總=S1+S2，即

但是從另一方面，從幾率的角度來看，某個分子出現在1，同時另一個分子出現在2，顯然是兩個相互獨立的事件，按照幾率相乘定理，它們同時出現的幾率

若兩個量乘積的函數等于兩個量函數之和，這樣的函數只可能是對數函數，即f(W)=lnW，則有

這就是著名的玻爾茲曼關系。它給出了熵的統計解釋，而且對平衡態和非平衡態都適用［8］。

由式(9)可得:dS=kdlnW

在有限變化的情況下，微分將由差分所代替，成為:

將式(10)代入式(4)，得到:

在一般情況下，以廢熱形式表示的不可用能Q，也可以用更一般的E來表示，即

這就是說，對于環境溫度是T0的孤立系統，不可用能與熱力學幾率對數的變化量成正比。由于△S≥0，所以總有△lnW≥0。除非系統已經達到平衡態，△S=0，△lnW=0，這時不可用能等于零。處于平衡態的系統，已經無能量能夠貶值。當然，這時也無能量能夠通過轉化對外作功了。只要系統在作功，能量的貶值，或者說不可用能的產生就是不可避免的。

2 熵增在物質和生命系統中的表現

仍然以水流為例考察一個物質系統。高處的水流下來變成了低處的水，水流的勢能轉化成為動能，這個動能可以推動水輪機作功，做過功的水就流向了低處，變成了幾乎不能再作功的水。同時，在水的流動過程中，也有一部分勢能轉化成為水流因摩擦而擴散出去的熱能中，這部分轉化為內能的能量不可能再轉化用來作功，成為不可用能［9］。

而這一切，都是在熵增大的過程中發生的。由于攪拌過的水的狀態熱力學幾率增大，導致熵的增大，使能量中的無用能增大，從而導致能量的貶值。

再來考察一個生命系統。生物體從環境中攝取物質和能量，才能使生命活動得以延續。同時，在此過程中，生物體同樣要將增大的熵以散熱等形式排出體外，以保證體內熵的平衡。生物體所排出的熱量，實際上就是無用的能量，就是能量的貶值部分。從統計物理學的角度來看，那就是，生命活動使生物體狀態的熱力學幾率增大，而散熱過程使生物體通過與環境的熱交換，使狀態的熱力學幾率減小，從而使二者達到一種動態的平衡。

這個問題還可以這樣理解:如果把生物體這個開放系統從環境中攝取的物質和能量看作是外界向系統內輸入的負熵流，那么這個負熵流將壓低系統的熵增，從而提高系統能量的“品質”，提高系統可利用能的大小。當然，這也只不過是延緩了系統走向平衡態的進程而已，一旦這種動態的平衡被打破，系統仍然會繼續向平衡態發展。

在國民經濟的發展中，建立一個人與自然和諧共生的環境友好型社會是非常重要的。提倡“低碳經濟”要求減少向環境中碳的排放，就是要提高能量的可利用度，壓低能量的退降。雖然完全能量意義上的“零排放”是不可能的，但是可以盡可能地減小不可利用能在總能量中所占的份額。轉變生產方式和消費方式，發展循環經濟，節約能源，提高熱利用的效率，積極發展和使用干凈的綠色能源，做到低消耗、低污染，這對于應對地球未來的氣候變化，保護人類的生存空間，都有著非常重要的意義。從理論上分析研究如何減小貶值能量，以更有效地利用我們有限的能量資源，使人類在一個生態文明的社會可持續地發展，這是一個有著實際應用價值的重要課題。

［1］關洪.物理學史選講［M］.北京:高等教育出版社，1994:114，225.

［2］菅原正巳.公害和熵增加［C］//熵理論的一場大辯論.成都:四川科學技術出版社，1993:342－344.

［3］菅原正已.水資源和熵［C］//熵理論的一場大辯論.成都:四川科學技術出版社，1993:345－347.

［4］陳熙謀，舒幼生，陳秉乾.能與熵［J］.物理教學，1997，(11).

［5］高德章.熵與不可用能初探［C］//熵與交叉科學.北京:氣象出版社，1988:43.

［6］陳光旨.熱力學統計物理基礎(上冊)［M］.桂林:廣西師范大學出版社，1989:49.

［7］F 瑞夫.統計物理學［M］.北京:科學出版社，1979:280.

［8］倪光炯，王炎森.物理與文化——物理思想與人文精神的融合(第2版)［M］.北京:高等教育出版社，2009:219.

［9］槌田敦.資源物理學［M］.上海:華東化工學院出版社.1991:94－95.

Entropy Increase Being Devaluation of Energy

HAN Feng
(Department of Physics and Electronic Engineering，Hechi University，Yizhou，Guangxi 546300，China)

According to the viewpoint of thermodynamics and statistical physics，an increase in the entropy of a system means the decrease in usable energy or the devaluation of energy.

thermodynamics and statistical physics;entropy increase;Boltzmann relation;usable energy;devaluation of energy

O414.11

A

1672－9021(2011)02－0022－04

韓鋒(1943－)，男，山西文水人，河池學院物理與電子工程系教授，主要研究方向:理論物理學、物理哲學。

2011－03－20

［責任編輯 劉景平］