無損動態檢測技術在映秀灣水電站災后評估中的應用

彭文明，王達會，張 琦，胡永勝

(中國水電顧問集團成都勘測設計研究院，四川 成都 610072)

1 前 言

1.1 問題的提出

“5.12”汶川地震發生后，當地基礎設施受損嚴重。映秀灣水電站處于地震震中映秀鎮，電站所屬的水工結構物在該次強震的作用下受到不同程度損傷。一般的水工建筑物埋設的監測儀器多是靜態儀器，如變位、應力、滲壓、滲流量監測儀等，震后這些儀器基準點可能發生漂移，不能很好地反映水工結構物存在的損傷情況，而對水工結構物的進行動態檢測可以彌補常規靜態監測存在的不足。然而，通常采用的動態監測方法，包括回彈法、超聲波法、地震波法、地質雷達法等，對于水工建筑物(特別是水下部分)損傷的檢測存在許多局限。尋找更有效的無損動態檢測技術手段對震后的映秀灣水電站進行損傷檢測、分析與綜合評價是十分必要的。

1.2 工程簡介

映秀灣水電站位于四川省汶川縣岷江上游干流上, 距映秀鎮上游約5km，為引水式發電水利工程，正常蓄水位以下庫容56萬m3，裝機容量135MW。工程等別為三等工程，工程規模為中型。擋水和泄洪建筑物、引水建筑物、發電廠房按3級建筑物設計，地震設防烈度為Ⅷ度。

2 攔河閘壩振動現場測試測點布置

為了量測映秀灣水電站攔河閘在水流自由泄流情況下的振動動位移，項目課題組于2008年8月24～27日對攔河閘1～5孔的閘墩進行了動位移測試，傳感器布置及信號采集系統連接見圖1、2。

該攔河閘各孔之間的分縫形式為閘墩中間分縫，對每孔閘墩進行測試時，左、右兩側各半個閘墩各同時布置動位移傳感器12個(其中10個水平、2個垂直)，同時在每孔的上、下游導墻上各布置2個水平向動位移傳感器。

圖1 攔河閘閘墩側面動位移傳感器布置示意

圖2 振動響應測試框圖

3 基于環境激勵的攔河閘壩結構振動模態識別

水工結構由于長期使用后老化、疲勞等原因，不少在役泄水結構存在各種病害與隱患，可能導致結構失穩或強度破壞。損傷會使水工結構的質量或剛度損失而引起動力特性發生變化，這都將在模態測量中有所反映。因此水工結構運行狀態健康診斷的核心技術之一就是如何通過各種技術手段獲取結構的模態參數指標。

工程實踐中，大部分水工結構(特別是泄水結構)在工作狀態下只受到環境激勵(如水流脈動激勵)，根據這些激勵源的輸入信號，測試大型水工結構在環境激勵下的工作模態參數，將為水工結構的健康診斷提供極大的便利。

3.1 基于奇異熵定階降噪的水工結構模態參數ERA時域識別法

在結構工作模態時域識別方法中，特征系統實現法(ERA)利用系統脈沖響應函數構造廣義Hankel矩陣，利用奇異值分解技術，得到系統的最小實現，從而得到最小階數的系統矩陣，以此為基礎可進一步識別系統的模態參數。該方法理論嚴密、技術先進且計算量小，是當今乃至目前最完善最先進的方法之一。但該法需事先確定Hankel矩陣的階次，而結構的工作模態階次事先是未知的。現將熵的概念引入系統識別領域[1-2]，利用奇異熵技術對原始信號進行消噪及結構工作模態定階，并結合ERA方法可有效地為水工結構系統工作模態定階并進行模態參數識別。

利用上述方法對結構在線工作模態參數識別的具體步驟如下：

(2) 利用NExT法[3]計算結構測點的脈沖響應函數；

(5) 最后根據已確定的階次確定系統矩陣A、輸入矩陣B和輸出矩陣C；

(6) 求解系統矩陣A的特征值，求得極點與留數，從而確定系統的模態參數。

3.2 基于頻域分解法(FDD)的水工結構模態參數識別頻域法

頻域分解法是僅利用結構輸出響應識別結構模態參數整體頻域識別方法，識別出的模態參數具有一致性，具有其他頻域法不可比擬的優點，可與時域法識別結果相互印證。

3.3 基于SSI算法的水工結構模態參數識別

基于虛假模態對不同參數模型比較敏感易變的原則，通過考察一些不同的參數模型，那些同時出現次數最多的、穩定的模態可以認為是系統的真實模態。

針對SSI具有Hankel矩陣的維數較難確定，可能丟失模態或產生虛假模態的缺點，對穩定圖剔除噪聲模態的方法進行如下改進[4]：

(1) 在利用奇異熵增量譜確定系統的模態階次后，把Hankel矩陣的行空間數據由imin增加到imax時(imax是個相對的較大值，要滿足j/i足夠大)，把計算得到的結果畫到二維坐標圖中(橫坐標為頻率值，縱坐標為Hankel矩陣的行塊數)，從而得到模態參數的穩定圖；

(2) 在穩定圖中若相鄰兩點的頻率和阻尼比在容許誤差范圍內，則認為是相同的；

(3) 可以根據所測試結構的具體情況加入阻尼比的判據準則，例如，結構阻尼比值通常大于10%或小于1%時，可以認為是虛假模態；

(4) 為了得到更為精確的識別結果，利用模態置信因子MAC指標進行虛假模態的判別。

經過以上四步改進，得到更為精確的穩定圖。運用“三步法”對水工結構的模態參數進行精確識別，步驟如下(如圖3所示)：

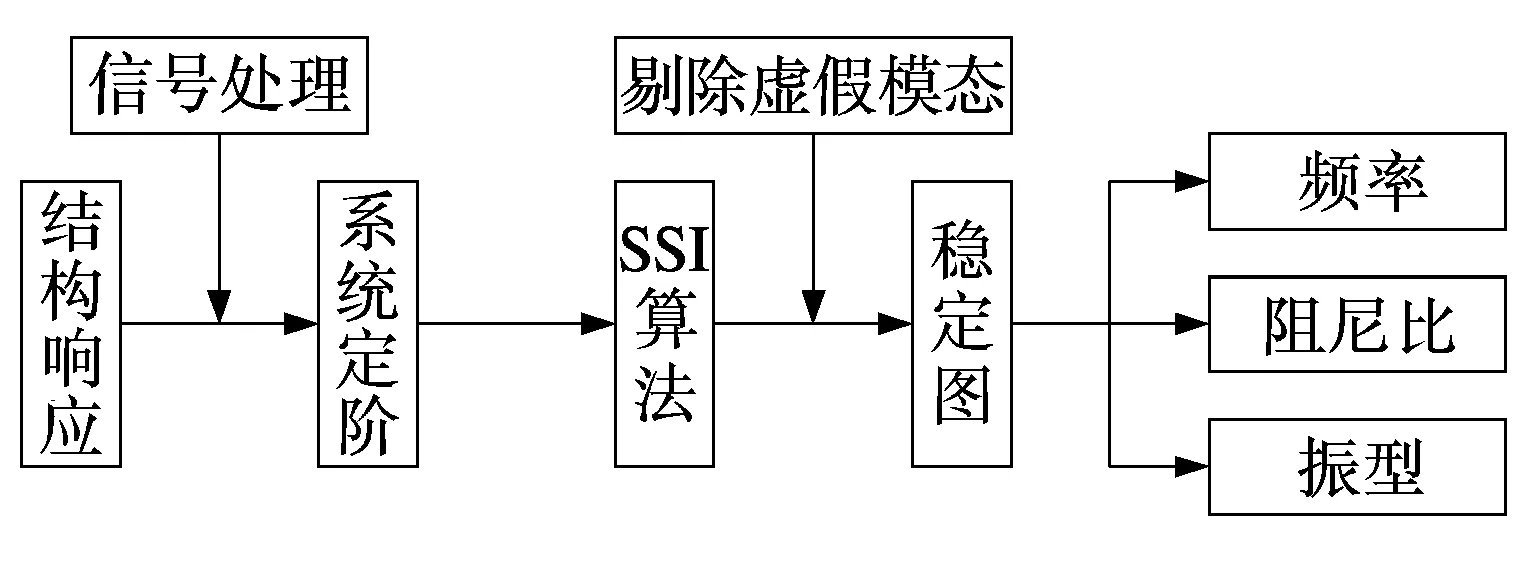
圖3 模態參數識別流程

第一步，用奇異熵增量對系統進行定階，使得定階的界線更加清晰和穩定；第二步，在系統階次明確的前提下，利用改進的穩定圖對虛假模態進行剔除，使得參數識別的結果更為準確可靠；第三步，將各階模態參數識別結果進行平均處理，最終得到更為精確的識別結果。

上述三種水工結構模態參數識別法均有較為嚴密的理論推導，并經過典型水流脈動荷載作用下水工結構數值算例R 驗證以及工程實踐檢驗[5-6]。從識別結果來看，各方法均能夠較精確地識別結構模態參數。

3.4 攔河閘壩模態參數識別

以攔河閘壩自由泄流時所采集到的數據為依據進行模態參數識別。以1號攔河閘為例說明。

3.4.1 測試信號的預處理

由于本次測試是利用結構在環境激勵下的特點采集數據，因此所采集的初始信號受一定的環境背景噪聲干擾，應予以剔除。1號攔河閘閘墩典型測點(1A)及下游導墻典型測點(13A)原始波形如圖4所示。

圖4 1A、13A測點的原始時程線

從原始測試數據波形上可以看出，信號受一定程度的低頻大波干擾，因此應當首先消除閘墩上以及上、下游導墻上所有測點原始信號的低頻大波干擾。由于大波信號主要表現為低頻，故采用高通濾波即可消除。1A及13A測點消除后的信號時程波形如圖5所示。

圖5 1A、13A測點低頻大波消除后的時程線(局部)

3.4.2 攔河閘振動模態參數識別

將干擾信號慮除后，分別利用ERA法、頻域分解法(FDD)、隨機子空間法(SSI)進行攔河閘結構模態參數識別，識別得出的前三階攔河閘結構頻率見表1。

從信號識別結果來看，1號攔河閘兩側閘墩的主要結構工作頻率有3階，兩側閘墩對稱，結構形式相同，因此識別結果相近，第一階工作頻率為3.7～4.2Hz左右，第二階工作頻率為8.3～8.9Hz左右，第三階工作頻率為12.4～13.1Hz左右。

表1 1號攔河閘結構工作模態參數識別結果

4 攔河閘壩結構的有限元模態分析

4.1 基本原理

4.1.1 結構振動的運動方程

結構的自振頻率和振型反映了結構的固有動力特性，確定它們的值是動力分析最基本的內容。結構用有限單元離散化后的運動方程可表示為：

(1)

式中M、C、K——分別為質量矩陣、阻尼矩陣、剛度矩陣；

δ——結點位移；

P(t)——動力荷載。

4.1.2 流固耦合的數值計算假定

用聲場分析考慮流固耦合作用，在求解結構的運動方程(1)時，需要考慮流體的N-S方程以及流體運動的連續方程。結構的離散化按普通固體結構有限元進行離散，流體結構按流體聲單元進行離散，并采用以下假定：(1)流體是可以壓縮的(即流體的密度隨壓力的變化而變化)；(2)不考慮流體的粘性；(3)不考慮流體的流動；(4)整個流體域的密度和壓力一致。

4.2 閘壩有限元模態分析

采用ANSYS大型有限元軟件進行攔河閘閘室結構模態分析。計算范圍及邊界條件：地基計算深度取1倍水閘高度，上、下游計算長度取1倍導墻高度；底板四周采用橫向支撐約束(即垂直于邊界的單向約束)；地基地面及四周采用全約束，即約束x、y、z方向位移；工作橋及啟閉機重量以附加質量的形式考慮。

攔河閘及地基結構計算材料參數：混凝土材料彈模E=2.55×104MPa,泊松比μ=0.167，材料密度ρ=2 500kg/m3；地基材料動模E=50MPa,泊松比μ=0.32，材料密度ρ=2 250kg/m3。

1號 攔河閘結構的有限元模型見圖6。

1號攔河閘結構模態計算結果見表2。

圖6 1號攔河閘結構有限元模型

表2 1號攔河閘結構模態計算結果 Hz

從計算結果來看，1號攔河閘閘墩一階振動頻率為3.84Hz(第2、3階)左右，閘墩二階振動頻率為8.3Hz(第5、6階)，三、四、五階振動頻率分別為15.9、16.3、16.7(第8、9、10階)；閘室整體豎向振動一階頻率為2.79Hz(也即閘室整體結構基頻)，閘室整體翻轉振動頻率為7.37Hz(第4階)，閘室兩側閘墩連同底板扭振頻率為12.6Hz(第7階)。

4.3 攔河閘結構損傷對自振頻率的影響

假定若干種破壞形式及破壞程度進行有限元計算，結合識別結果綜合分析當前結構的完整性。攔河閘損傷的模擬主要考慮在閘墩水下部分不同位置設置不同深度的裂縫，共分三種情況，即：(1)閘墩內側水下不同部位不同程度損傷(裂縫深0.5m或1m、順水流向長12m或24m、距底板1m或2m的不同組合)；(2)閘墩外側不同部位不同程度損傷(與(1)同樣的組合)；(3)底板不同位置損傷。共模擬28種損傷工況。

對損傷工況進行有限元模態分析，損傷前與損傷后的頻率變化對比發現，不同位置不同程度的損傷對閘室結構頻率的影響規律主要表現在：(1) 裂縫越長、越深，對振動頻率的影響越大；(2)無論裂縫沿水流方向長度如何，相比閘墩前三階振動頻率，裂縫對閘墩一階振動頻率的影響最大，對閘墩第二階振動頻率的影響次之，對閘墩第三階振動頻率影響最小；(3)總體上看，在損傷情況下振動頻率下降約2%～20%，閘墩第二、三階下降在2%～4%左右，第一階下降5%～20%。

5 閘壩結構健康狀態評估

結構損傷對攔河閘高階頻率影響較小，對第一階頻率影響較大。為評估閘壩結構的健康狀況，將各孔攔河閘在泄流激勵下的模態識別結果與基于有限元數值計算前三階模態頻率結果進行對比，結果見表3。

表3 攔河閘結構識別與有限元計算比較

從識別結果與計算結果來看，各孔攔河閘結構有限元計算頻率與識別結果基本相近，各閘平均偏差均小于2%(4號攔河閘平均偏差最大，為1.72%)。根據攔河閘結構損傷對自振頻率的影響分析可知，閘墩最輕微損傷工況(裂縫深0.5m、長12m)時，閘墩振動頻率比完好結構下降也超過2%，因此可以判斷各孔攔河閘原型真實結構狀態與有限元模擬完好結構狀態相似，閘墩與底板整體性較強。值得一提的是，識別結果與有限元計算結果都存在一定的誤差(一般誤差約2%)，但對于水閘這類較為簡單的結構，這些誤差相對要小很多，因此，可以通過識別值與有限元計算結果進行對比分析判斷。

6 結 論

通過對攔河閘原型動力測試、完好結構與有損傷結構有限元模態仿真計算結果分析，震后攔河閘的真實動力特性與完好結構有限元模擬相似，可判斷攔河閘結構整體性較好，未出現影響攔河閘整體結構性的損傷[7]。

[1] 王安麗,史志富,張安.基于熵的空中目標識別模型及應用[J].火力與指揮控制,2005,30(2):110-112.

[2] 練繼建，李火坤，張建偉.基于奇異熵定階降噪的水工結構振動模態ERA識別方法[J].中國科學,E輯,2008(7).

[3] 傅志方.振動模態分析與參數辨識[M].北京:機械工業出版社,1990.

[4] 練繼建，張建偉，李火坤，馬斌.泄洪激勵下高拱壩模態參數識別研究[J].振動與沖擊，2007,26(12):101-105.

[5] 王兆輝,樊可清,李霆.系統辨識在橋梁狀態監測中的應用[J].中南公路工程,2006,31(3):159-163.

[6] 三峽水利樞紐廠壩隔(導)墻泄洪振動水彈性模型試驗研究[R].天津：天津大學水利水電工程系，1997.

[7] 映秀灣水電站攔河閘及廠房災后評估檢測研究報告[R].天津：天津大學建筑工程學院，2008.