工業(yè)生產(chǎn)中一個帶有拒絕費用的工件排序問題研究

馮 琪，楊麗華

（中原工學院，鄭州450007）

工業(yè)生產(chǎn)中一個帶有拒絕費用的工件排序問題研究

馮 琪，楊麗華

（中原工學院，鄭州450007）

在工業(yè)生產(chǎn)中，生產(chǎn)決策者為了獲得最大利潤，可能接收一個工件，也可能拒絕一個工件．為了解決哪些工件應該被接收，哪些工件應該被拒絕問題，本文研究了工業(yè)生產(chǎn)中一個帶有拒絕費用的工件排序問題，對該問題設計了一個動態(tài)規(guī)劃算法．

排序；拒絕；動態(tài)規(guī)劃算法

所謂排序，就是在一定的約束條件下對工件和機器按時間進行分配和安排加工次序，使一個或多個指標達到最優(yōu)．作為運籌學和管理學的一個重要分支，機器排序理論有著深厚的背景和廣闊的應用前景．例如，如果我們把現(xiàn)有的資源（如人力、資金、工具等）當成機器，把所要完成的任務當成工件，那么其他領域的許多問題都可以轉(zhuǎn)化成一個機器排序問題．目前，關于排序理論的研究成果已經(jīng)應用在許多不同的領域，包括計算機科學及工程、供應鏈管理、物流運輸?shù)阮I域．因此，從廣義上來說，機器排序可以理解為最優(yōu)地分配有限資源以完成給定的任務．

在大多數(shù)經(jīng)典的排序文獻中，都是基于以下假設：所有的工件都必須在機器上加工，不允許拒絕任何工件．然而，在現(xiàn)實中這些假設并非總是成立的．由于資源的有限性，在實際中生產(chǎn)決策者經(jīng)常會拒絕一些耗費資源且利潤較低的工件．如果拒絕一個工件，有時候基于信用或其他因素，不得不支付一個確定的拒絕費用．

可拒絕工件的排序問題是一種新的排序模型．關于這方面的研究還比較少．Bartal Y等人首先考慮了帶有拒絕費用的排序問題，他們的目標是把被接收工件的最大完工時間與所有被拒絕工件總的拒絕費用之和最小化．對于在線情形，他們給出了一個在線算法，并且證明了這個在線算法有最好的競爭比2．618；對于離線情形，他們給出了一個近似比為2－的近似算法和一個多項式時間近似方案（這里m是平行機機器數(shù)量）［1］．自此以后，帶有拒絕費用的工件排序問題受到越來越多的關注．對上述的工件在線排序問題，在所有的工件加工允許被中斷的情況下，Seiden S給出了一個競爭比約為2．387 4的在線算法［2］．Hoogeveen H等人考慮了允許加工中斷的工件離線排序問題，他們證明了這個問題是NP－困難的，并給出了一個全多項式時間近似方案［3］．Engles D W等人考慮了工件可拒絕的單機排序問題，目標是把被接收工件總的完工時間與所有被拒絕工件總的拒絕費用之和最小化；他們證明了這個問題是NP－困難的，并給出了一個全多項式時間近似方案［4］．Epstein L等人考慮了具有單位長度的工件的單機在線排序問題，目標是把被接收工件總的完工時間與所有被拒絕工件總的拒絕費用之和最小化，他們給出了一個競爭比約為1．866的在線算法，并且證明了任何確定的在線算法的競爭比至少為1．637 84［5］．Lu L F等人也對帶有拒絕費用的工件排序問題做了大量的研究，對不同的機器環(huán)境進行了分析和探討，并且得出了一系列結(jié)論［6－9］．

對工業(yè)生產(chǎn)中帶有拒絕費用的工件排序問題，還有大量的挑戰(zhàn)性的問題有待解決．本文研究了這一領域中的一個排序問題，探討了它的計算復雜性，并且設計了一個動態(tài)規(guī)劃算法．

1 排序問題的描述

對本文所考慮的帶有拒絕費用的工件排序問題描述如下：

有1臺機器，n個待加工的工件J1，…，Jn．并且每個工件Jj有一個加工時間pj和一個拒絕費用wj．工件Jj或者被拒絕并且支付一個確定的拒絕費用wj，或者被接收并安排在機器上加工．目標是使被接收工件總的完工時間與所有被拒絕工件總的拒絕費用之和達到最小．

2 排序問題的記號與概念

我們定義A和R分別為所有被接收工件的集合和所有被拒絕工件的集合．采用Graham P L等人提出的排序問題的一般記號［10］，把這個問題記為

根據(jù)1979年Graham P L等人提出的工件排序問題的三參數(shù)表示法［10］，我們使用α｜β｜γ來表示一個排序問題．在這里，α域表示機器的數(shù)量、類型和環(huán)境；β域表示工件的特征和約束；γ域表示要優(yōu)化的目標．在本文中，α域、β域和γ域中的參數(shù)分別表示如下：

（1）α域：1表示單機，并且一次只能加工一個工件．

（2）β域：J1，…，Jn表示n個需要加工的工件；pj表示工件Jj的加工時間；wj表示工件Jj的拒絕費用；reject表示工件允許被拒絕且每個被拒絕的工件要支付一個拒絕費用wj．

（3）γ域：Cj表示工件Jj的完工時間，表示

j被接收工件總的完工時間；wj表示被拒絕工件Jj的拒絕費用，表示被拒絕工作總的拒絕用費；表示被接收工件總的完工時間與被拒絕工件總的拒絕費用之和．

3 排序問題的求解

針對所研究的排序問題，我們將設計一個動態(tài)規(guī)劃算法來解決．

3．1 動態(tài)規(guī)劃算法的思想

（1）動態(tài)規(guī)劃方法的關鍵在于正確地寫出基本的遞推關系式和恰當?shù)倪吔鐥l件．要做到這一點，必須先將問題的過程分成幾個相互聯(lián)系的階段，恰當?shù)剡x取狀態(tài)變量和決策變量及定義最優(yōu)值函數(shù)，從而把一個大問題轉(zhuǎn)化成一組同類型的子問題，然后逐個求解．即從邊界條件開始，逐段遞推尋優(yōu)．在對每一個子問題的求解中，均利用了它前面的子問題的最優(yōu)化結(jié)果，依次進行，對最后一個子問題求解所得到的最優(yōu)解就是整個問題的最優(yōu)解．

（2）在多階段決策過程中，動態(tài)規(guī)劃方法是既把當前一階段和未來各階段分開，又把當前效益和未來效益結(jié)合起來考慮的一種最優(yōu)化方法．因此，每階段的決策是從全局來考慮的，與單獨考慮本階段狀態(tài)得出的決策一般是不同的．

（3）在求整個問題的最優(yōu)策略時，由于初始狀態(tài)是已知的，而每階段的決策都是該階段狀態(tài)的函數(shù)，故最優(yōu)策略所經(jīng)過的各階段狀態(tài)便可逐次變換得到，從而確定最優(yōu)路線．

3．2 動態(tài)規(guī)劃算法

根據(jù)引理1，對工件重新標號，使得p1≤…≤pn．下面給出一個定理，在這個定理中，工件的最優(yōu)加工次序與引理①中的工件的最優(yōu)加工次序有密切的關系

定理1：在O（n2）時間內(nèi)能得到問題的最優(yōu)解．

對定理1證明如下：

設f（j，m）是所考慮工件為Jj，…，Jn且被拒絕工件的個數(shù)為m時所對應的最優(yōu)目標函數(shù)值．

現(xiàn)在，考慮工件為Jj，…，Jn且被拒絕工件的個數(shù)為m時的一個最優(yōu)排序．在這個排序中，僅僅有下面兩種可能的情形：

情形1：工件Jj被拒絕并且支付一個確定的拒絕費用wj．

由于工件Jj被拒絕，則對于工件集Jj－1，…，Jn，所有被拒絕工件的個數(shù)為m－1，工件Jj對目標函數(shù)的貢獻是wj，因此，有f（j，m）＝f（j－1，m－1）＋wj．

情形2：工件Jj被接收并安排在機器上加工．

由于工件Jj被接收，則對于工件集Jj－1，…，Jn，所有被拒絕工件的個數(shù)為m，工件Jj對目標函數(shù)的貢獻是pj，因此，有f（j，m）＝f（j－1，m）＋pj．

綜合上述兩種情形，給出下面的動態(tài)規(guī)劃算法DP．這種算法為：

（1）邊界條件：

f（1，0）＝pj，f（1，1）＝wj；且在m≠0，1時，f（1，m）＝∞．

（2）遞推函數(shù)：

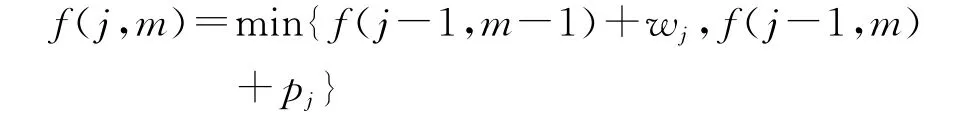
（3）最優(yōu)值：

min｛f（n，m），1≤m≤n｝

由于1≤j≤n，且1≤m≤n，至多有O（n2）個不同的狀態(tài)變量．并且每次迭代均花費一個常數(shù)時間．因此，動態(tài)規(guī)劃算法DP的時間復雜性為O（n2），即可以在O（n2）時間內(nèi)得出問題的最優(yōu)解．

4 結(jié) 語

本文研究了工業(yè)生產(chǎn)中一個帶有拒絕費用的排序問題，對該問題設計了一個動態(tài)規(guī)劃算法，探討了它的計算復雜性．這對于幫助決策者在加工產(chǎn)品時取舍工件提供了理論依據(jù)．

［1］Bartal Y，Leonardi S，Spaccamela A M，eta l．Multiprocessor Scheduling with Rejection［J］．SIAM Journal on Discrete Mathematics，2000，13：64－78．

［2］Seiden S．Preemptive Multiprocessor Scheduling with Rejection［J］．Theoretical Computer Science，2001，262：437－458．

［3］Hoogeveen H，Skutella M，Woeginger G J．Preemptive Scheduling with Rejection［J］．Mathematics Programming，2003，94：361－374．

［4］Engels D W，Karger D R，Kolliopoulos S G，eta l．Techniques for Scheduling with Rejection［J］．Journal of Algorithms，2003，49：175－191．

［5］Epstein L，Noga J，Woeginger G J．On－line Scheduling of Unit Time Jobs with Rejection：Minimizing the Total Completion Time［J］．Operations Research Letters，2002，30：415－420．

［6］Lu L F，Zhang L Q，Yuan J J．The Unbounded Parallel Batch Machine Scheduling with Release Dates and Rejection to Minimize Makespan［J］．Theoretical Computer Science，2008，396：283－289．

［7］Lu L F，Cheng T C E，Yuan J J，eta l．Bounded Single－machine Parallel－batch Scheduling with Release Dates and Rejection［J］．Computers and Operation Research，2009，36：2748－2751．

［8］Zhang L Q，Lu L F，Yuan J J．Single Machine Scheduling with Release Dates and Rejection［J］．European Journal of Operational Research，2009，198：975－978．

［9］Zhang L Q，Lu L F，Yuan J J．Single－machine Scheduling under the Job Rejection Constraint［J］．Theoretical Computer Science，2010，411：1877－1882．

［10］Graham P L，Lawler E L，Lenstra J K，eta l．Optimization and Approximation in Deterministic Machine Scheduling：A survey［J］．Annals of Discrete Mathematics，1979，5：287－326．

［11］Baker K R．Introduction to Sequencing and Scheduling［M］．New York：John Wiley ＆Sons，1979．

Study on the Scheudling Problem with Rejiction Cost in Industrial Production

FENG Qi，YANG Li－h(huán)ua
（Zhongyuan University of Technology，Zhengzhou 450007，China）

In industrial production，decision－makers either accept a job or reject a job to obtain the maximum profit．In order to solve the problem which jobs should be accepted and which jobs should be rejected，a scheduling problem with rejection cost in industrial production in this paper is researched．A dynamic programming algorithm for the problem is designed．

scheduling；rejection；dynamic programming algoriathm

O223

A

10．3969／j．issn．1671－6906．2011．05．001

1671－6906（2011）05－0001－03

2011－09－15

國家自然科學基金項目（10971201；61070229）

馮 琪（1975－），女，河南周口人，講師，博士生．