格上基于身份的代理環簽名方案
張利利,馬艷琴
(黃河科技學院信息工程學院,河南鄭州 450063)
0 引 言
1984年,Shamir[1]提出基于身份的公鑰密碼體制,其簡化了基于證書的公鑰體制負擔最重的密鑰管理過程.1996年,Mambo等[2]提出代理簽名,利用代理簽名,原始簽名人可以將他(她)的簽名權委托給代理簽名者,對任何消息代理人都可以進行簽名,任何人只要知道原始簽名人的公鑰就可以對代理簽名進行驗證.2001年,Rivest等[3]提出環簽名,其實際上是一種簡化的群簽名,它僅包括環成員而沒有管理者,不需要群建立過程,也無法撤銷真實簽名者的匿名性,簽名驗證者可以確定簽名來自某個環成員,但無法確定簽名者的具體身份,因而可以有效地保護實際簽名者的隱私權.根據對代理人保持匿名的應用,2003年,Zhang[4]提出了代理環簽名的方案,并給出第一個基于身份的代理環簽名方案:當授權人將簽名權利授予很多代理人時,這些代理人組成了一個代理人集合,每個代理人都可以代替授權人執行簽名操作,并且可不被任何人(包括授權人)揭開他的身份.2006年,楊少春[5]提出了一種更加高效的代理環簽名方案,計算量得到很大的改善.但是,這些代理環簽名方案大部分都是基于大整數分解和離散對數問題的,在量子計算機得到應用的前提下,大整數分解問題和離散對數問題都可以利用多項式時間算法解決.因此,設計能抵抗量子攻擊的代理環簽名方案成為該領域需解決的問題.近年來,基于格構造的新型密碼系統因具有運算簡單(通常只需要線性運算)、能抵抗量子攻擊和存在最壞情況下的隨機實例等特點,成為公鑰密碼領域的研究熱點,并取得了一系列的研究成果[6-9].本研究基于格上的SIS和 ISIS問題的困難性,利用原像抽樣函數[6]和格基代理算法[9]構造了一個格上基于身份的無可信中心的代理環簽名方案.
1 基礎知識
1.1 格
設 b1,b2,…,bn是Rm上一組的量,令B=[b1, b2,…,bn]? Rm×n,則由 B生成的n為格定義為,
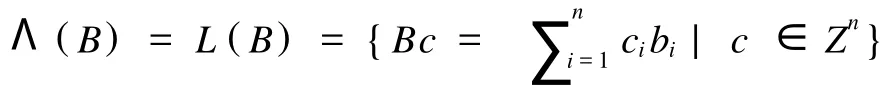
Λ(B)的正交格定義為,
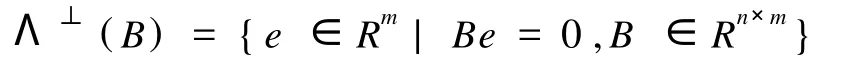
設ω是一個向量,ω的lp-范數定義為,

當p=2時,稱作歐幾里得范數,簡記為‖ω‖.
1.2 格上的困難問題
(1)SVP問題(最短向量問題).設A是格的一組基,SVP問題就是在格上尋找一個非零向量u,滿足任意格上的向量v,有 ‖u‖≤‖v‖成立.其中 ‖·‖為給定的范數.
(2)SIS問題(小整數解問題).給定整數 q,實數β,矩陣A∈Zn×mq,尋找一個非零向量 e,滿足Ae= 0modq,且 ‖e‖≤β.
(3)ISIS問題(非齊次小整數解問題).給定整數q,實數β,向量y∈Zmq,矩陣A∈Zn×mq,尋找一個非零向量e,滿足Ae=ymodq,且 ‖e‖≤β.
1.3 格上的多項式時間算法
由于SISq,m,rm是困難的,若 A∈Zn×mq,可得格上的陷門函數[6],
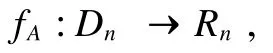
其中,fA(e)=Aemodq,Dn={z∈Zn|‖e‖≤r m},Rn= Zqn,輸入分布為 DZm,s.
基于原像抽樣函數,文獻[6]給出格上基于原像抽樣的多項式時間算法:
(1)TrapGen(1n).算法 TrapGen(1n)輸出(A, B),其中,矩陣 A在Znq×m接近均勻分布,矩陣B是Λ⊥(A)的小基.
(2)Sample D(A;r).從分布DZm,r中選取向量e,且fA(e)=Aemodq接近于Rn上均勻分布.
(3)Sample ISIS(A;B;y;r).輸入矩陣 A ∈Zn×m,Λ⊥(A)的小基B,向量y∈Zm和r>0,qqSample ISIS(A;B;y;r)輸出非零向量e,e為接近分布 DΛ⊥(A),r.
1.4 格基代理算法
格基代理算法[10]是一種由較小維數的格和基向量構造更大維數的格和基向量的算法.令 n,q, m,k為正整數,并且 q≥2,m≥5nlogq,格基代理算法ExtBasis和RandBasis描述如下:
(1)ExtBasis(S,A=A1‖A2).輸入矩陣 A1∈Zqn×m,任意矩陣A2∈Znq×m1,Λ⊥(A1)的基S1,算法⊥~ExtBasis輸出 Λ(A)的基 S,其中,‖S1‖=~‖S‖.
(2)RandBasis(A,S,r).輸入矩陣 A ∈ Znq×m, Λ⊥(A)的基S和參數r≥‖S‖ω( nlogq),算法RandBasis輸出的Λ⊥(A)的S′,其中,‖~S′‖≤r m,由S′得不到S的任何信息.
2 格上基于身份的代理環簽名方案
下面主要描述利用格上的難題和格基代理技術構造基于身份的代理環簽名方案.方案中的參數設置如下:令 n,q,m,k為正整數,并且 q≥2,m≥flogn,L~≥O( nlogq),r≥L~ω( logn).設 B1, B2,…,Bl為l個代理人,H1:{0,1}*→{0,1}n,H2: {0,1}*→{0,1}n×m為兩個安全的Hash函數,m′= (l+1)m.
2.1 系統建立
原始簽名人利用算法 TrapGen(1n)輸出(A0, S0),其中,A0在Znq×m接近均勻分布,S0是Λ⊥(A0)的小基.類似的,代理人Bi利用算法TrapGen(1λ)輸出(Ai,Si),Ai在Znq×m接近均勻分布,Si是Λ⊥(Ai)的小基,A0,S0分別為原始簽名人公鑰和私鑰,Ai, Si分別代理簽名人Bi的公鑰和私鑰.
2.2 代理密鑰的生成與驗證
2.2.1 代理密鑰的生成.
原始簽名人利用代理簽名人Bi的身份信息IDi∈{0,1}*為 Bi生成代理密鑰,
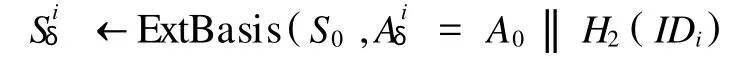
其中,Siδ為Λ⊥(Aiδ)的基.然后,將 Siδ發給Bi,i=1 ,2,…,l.
2.2.2 代理密鑰的驗證.
Bi驗證:①Siδ∈ Z2m×kq,k=2m- rank(Aiδ);②AiδSiδ=0modq是否成立,若成立,Bi接受Siδ為代理密鑰,否則,拒絕.
2.3 代理環簽名的生成
l個代理簽名人構成一個環,任何代理人Bi利用他的私鑰Si和代理密鑰Siδ均可以為原始簽名人生成代理環簽名.假設真正的簽名人為第 k個代理人Bk,待簽消息M ∈{0,1}*,簽名步驟如下:
(1)由私鑰Sk,Bk利用算法ExtBasis(Sk,A′δ= Ak‖A1‖‖A2‖…‖Ak-1‖Ak+1‖…‖Al)生成S′,對矩陣A′做列換,化A′為A=A1‖A2‖…‖Ak+1‖‖…‖Al,S′做相應的變換化為S,且 S為Λ⊥(A)的基.
(2)由代理密鑰 Siδ,Bk利用算法 ExtBasis(Siδ, A′δ=A0‖H2(IDk)‖…‖H2(IDk-1‖H2(IDk+1)‖…‖H2(IDl))生成 S′δ,將A′δ化為Aδ=A0‖(H2(ID1)‖…‖H2(IDk-1)‖H2(IDk)‖H2(IDk+1)‖…‖H2(IDl)),S′δ做相應的變換化為 Sδ,Sδ為Λ⊥(Aδ)的基.
(3)計算y= H1(M);
(4)利用SampleISIS(A;S;y;r)生成的向量 e,若 ‖e‖≥s m′或e=0,重新生成e.
(5)利用SampleISIS(Aδ;Sδ;y;r)生成的向量eδ,若 ‖eδ‖≥s m′-1或eδ=0,重新生成eδ.
(6)Bk輸出環簽名(M,eδ,e,L),其中,L = {B1,B2,…,Bl}.
2.4 簽名驗證
驗證者收到代理環簽名(M,eδ,e,L)后,驗證下列條件是否成立:
(1)e≠0,eδ≠0,‖eδ‖≤s m′-1,‖e‖≤s m′,
(2)(A1‖A2‖…‖Al)e=0modq,
(3)A0‖H2‖(ID1)‖H2(ID2)‖…‖H2(IDl)eδ=0modq.
若成立,驗證者接受(M,eδ,e,L)為有效的代理環簽名,否則,拒絕.
3 方案分析
3.1 安全性分析
3.1.1 匿名性.
簽名(M,eδ,e,L)是代理環中的某個代理人利用格上一個小基和算法SampleISIS得到的向量.其中,簽名過程中一個小基是代理人利用私鑰通過基擴展算法生成的,具有很好的隨機性,故該小基不會泄露簽名人任何信息.另外,算法的構造是利用抽樣算法SampleISIS得的,所得的結果(eδ,e)近似服從高斯分布,并沒有泄露該小基的相關信息.由于簽名結果和簽名過程中小基的這兩個主要信息都不會泄露簽名人的任何信息,所以簽名方案滿足匿名性.
3.1.2 不可偽造性.
定理1 基于格上的SIS難題,本研究的代理環簽名方案滿足存在性不可偽造性

定理的證明分兩部分,一部分是代理環簽名中eδ的不可偽造性,一部分是代理環簽名中 e的不可偽造性.下面僅給出第二部分證明,第一部分證明類似.
對于任意的矩陣,
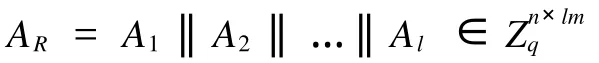
其中,A1,…,Al∈Zqn×m,0 (1)1≤i≤l,令Ai為代理環中第i人的公鑰; (2)l+1≤i≤Q,利用算法TrapGen(1n)輸出(Ai,Si),令Ai為代理環中第i人的公鑰,Si為代理環中第i人的私鑰. 將環成員的公鑰聯立所得矩陣A1‖A2‖…‖AQ發給 F. Hash詢問.對于任意的消息 mi,S隨機選擇ei←Sample D(AR;r),將 yi=AReimodq發送給F,并將(mi,ei,yi)存儲于列表L1. 簽名詢問.收到 F的簽名詢問(j,mi,Ri),(mi, ei,Ri)若Ri=R,S在列表L1查找(mi,ei,yi),將ei返回給 F,并將(mi,ei,Ri)存儲于列表L2;若 Ri≠R且l+1≤j≤Q,則S在列表L1查找(mi,ei,yi),將δi←Sample ISIS(ARi,ExtBasis(Sj,ARi),yj,r)返回給 F,并將(mi,δi,Ri)存儲于列表L2;若 Ri≠R且1≤j≤l,則S在列表L1查找(mi,ei,yi),任選k∈Ri,將δi←Sample ISIS(ARi,ExtBasis(Sk,ARi), yj,r)返回給 F,并將(mi,δi,Ri)存儲于列表L2. 若 F以ε的概率輸出一個偽造代理環簽名(j*, m*,R*,δ*),若R*≠R,S放棄;若R*=R,S在列表L1查找(m*,e*,y*),顯然,y*= ARe*= ARδ*modq,若e*≠δ*,則AR(e*-δ*)=0modq,‖e*-δ*‖≤2r lm,即,e*-δ*為SISAR,lm,2r的一個解.又因為 R*=R的概率為, 所以,算法 S解決SISq,lm,2rlm的難題的概率至少為, 令m=cnlogq,其中,c為常數,l為代理環成員個數,則本研究所提出的代理環簽名方案的公鑰長度、代理成員的私鑰長度、代理環簽名長度如表1所示. 表1 本文代理環簽名方案的效率分析 由表1可見:(1)與一般基于數論的代理環簽名相比,本研究提出的方案設計中僅僅使用到了小整數的模加和模乘運算,所以方案計算效率較高;(2)一般的基于身份的簽名方案,需要有可信中心為簽名人生成簽名私鑰,但在本研究的簽名方案中,任何簽名人均可以利用格上基于原像抽樣函數的算法TrapGen為自己生成簽名密鑰,不需要可信中心;(3)和文獻[10]環簽名相比,本方案的公鑰長度、代理成員的私鑰長度、代理環簽名長度更短,整體運算效率更高. 本文利用格上的格基代理算法和原像抽樣函數,在格上構造了一個基于身份的無可信中心的代理環簽名方案.基于格上SIS問題的困難性,本方案滿足匿名性和不可偽造性,與其他代理環簽名方案相比,本方案具有在量子計算環境下依然安全的優點. [1]Shamir A.Identity Based Cryptosystems and Signature Schemes [C]//Advances in Cryptology-Crypto’84.Santa Barbara,USA: Springer-Verlag,1984:48-54. [2]Mambo M,Usuda K,Okamoto,E.Proxy Signatures for Delegating Signing Operation[C]//Proceedings of the3rd ACM Conference on Computer and Communications Security.New Y ork:ACM Press,1996:48-57. [3]Rivest R,Shamir A,Tauman Y.How to Leak a Secret Advances in Cryptology[M].Heidelberg:Springer-Verlag,2001. [4]Zhang F,Naini R S,Lin C Y.New Proxy Signature,Proxy Blind Signature and Proxy Ring Signature Scheme from Bilinear Pairings[C]//Cryptology ePrint Archive Report2003/117.http:// eprint.iacr.org/2003/104/. [5]楊少春,郎為民.基于身份和雙線性對的代理環簽名方案[J].微計算機信息,2006,14(12):79-81. [6]Gentry C,Peikert C,Vaikuntanathan V.Trapdoors for Hard Lattices and New Cryptographic Constructions[C]//STOC’2008. Victoria,Canada:IEEE Press,2008:197-206. [7]Alwen J,Peikert C.Generating Shorter Bases for Hard Random Lattices[C]//STACS’2009.Freiburg,Germany:IEEE Press, 2009:75-86. [8]Wang Jin,Sun Bo.Ring Signature Cchemes from Lattice Basis Delegation[J].Information and Communications Security,Lecture,2011,7043(1):15-28. [9]Peikert C.Bonsai Trees[EB/OL].[2009-07-19].http:// eprint.iacr.org.2009. [10]王鳳和,胡予濮,王春曉.格上基于盆景樹模型的環簽名[J].電子與信息學報,2010,32(10):2400-2403.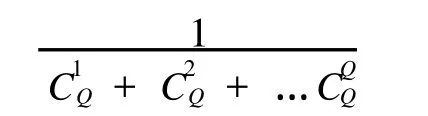

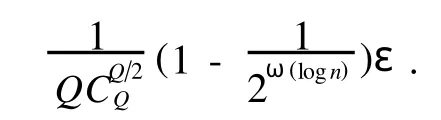
3.2 效率分析

4 結 論

