基于DRP的環形網絡控制系統穩定性分析

阮偉，陳根，劉國安

（浙江中控研究院有限公司，杭州310027）

由浙江大學、浙江中控技術股份有限公司聯合北京東土科技股份有限公司、上海自動化儀表有限公司提出的分布式環形網絡冗余技術（DRP），解決了傳統主從式環形網絡冗余恢復技術存在的故障風險高度集中的問題，實現了網絡化控制系統的高可用性。該技術被國際電工委員會IEC正式接收為國際標準IEC62439。

筆者在分析DRP的基礎上，建立了環網故障切換模型，并結合網絡化控制系統丟包穩定性模型，對基于DRP的環形網絡控制系統穩定性進行了分析，得出環形網絡化控制系統穩定性條件，并提出了構建穩定的、基于DPR的環形網絡控制系統的方法。

1 DRP協議原理

1.1 DRP環形網絡控制系統

基于DRP的環形網絡控制系統中的傳感器、控制器及執行機構，通過支持DRP協議的交換設備實現互聯，如圖1所示。

在環形網絡系統中普遍采用禁用備用路徑的方式，從而避免了由于數據在環網內無休止的回環而形成廣播風暴。圖1中的交換設備1與交換設備8之間存在物理通路。但是，該物理通路不進行數據傳輸，在邏輯上形成斷路。因此，該環形拓撲在邏輯上退化為線性結構，有效避免了廣播風暴的產生。

1.2 DRP的故障探測和恢復機理

在DRP環形網絡控制系統中，通信時間被分成多個宏周期，如圖2所示。

為了實現快速的故障探測和恢復，DRP同時采用環路探測和鏈路探測技術，分別針對交換設備故障和物理鏈路故障進行探測，并根據故障探測的結果實現快速的故障切換。

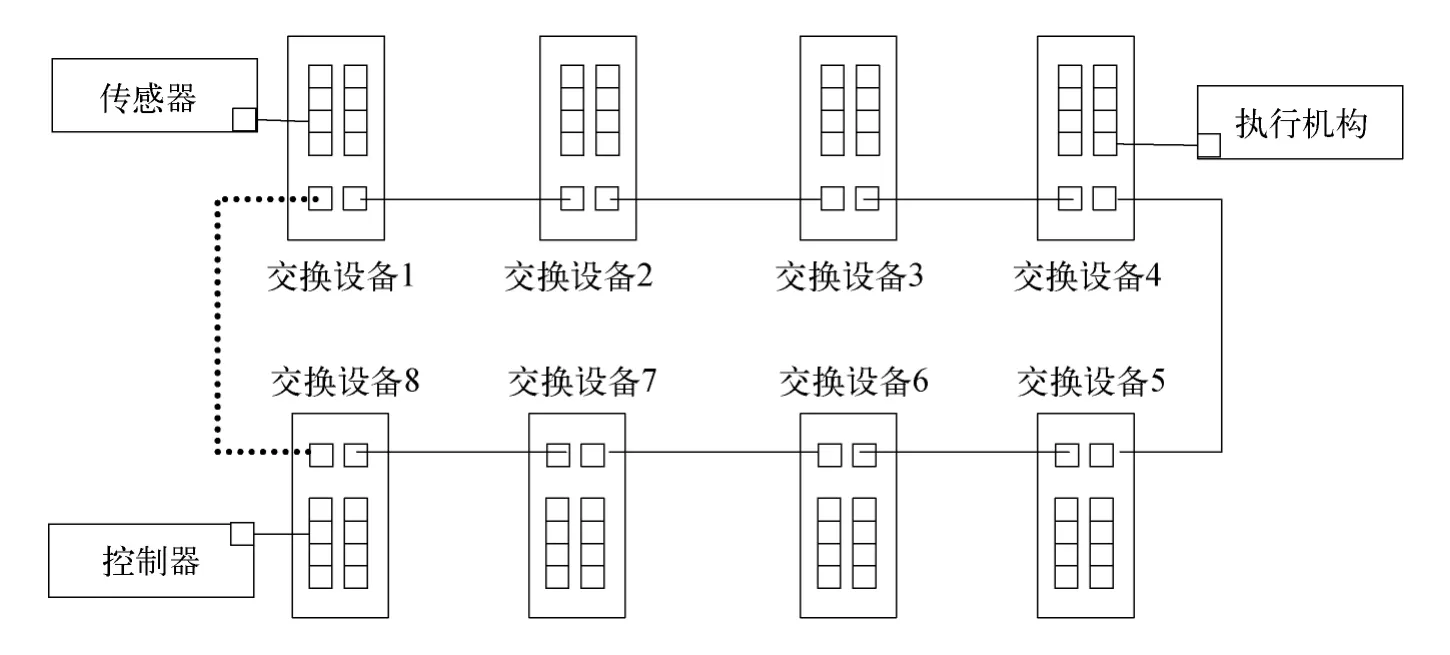
圖1 基于DRP的環形網絡控制系統結構

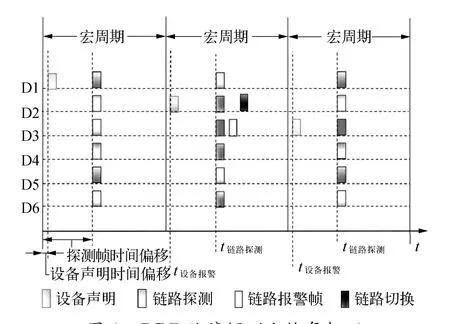
圖2 DRP故障探測和恢復機理

在一個宏周期內，t設備報警只有一個交換設備廣播鏈路報警幀進行環路故障探測。而每個交換設備節點在t鏈路探測發送鏈路探測幀，同時進行一次鏈路故障探測。

2 DRP故障恢復時間模型

在故障情況下，為了保證控制系統的穩定性，需要分析DRP方法的最大故障恢復時間。要求控制系統在故障恢復時間內，仍然能夠保持系統穩定。根據DRP進行故障探測和恢復的原理，建立DRP系統故障恢復時間模型。

DRP環形網絡控制系統的故障恢復時間：

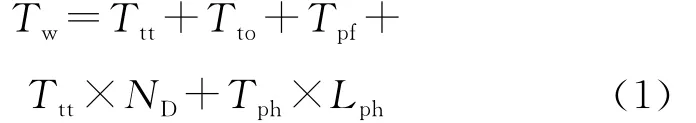
式中：Tw——最大故障自恢復時間；Tti——兩個Linkcheck幀發送之間的時間，也就是一個Macrocycle；Tto——接收Linkcheck的延時，代表從一個設備發送出這個數據幀，經過最大邏輯鏈路路程以后的收到時間；Tpf——在交換設備節點內部對DRP幀進行處理的延時（包括交換設備的接收相應延時和處理器的處理延時）；Ttt——交換設備節點內部DRP幀發送延時；Tph——1km距離的雙絞線傳送延時；Lph——DRP網絡內雙絞線的長度；ND——DRP網絡內交換節點的數量。

3 DRP故障過程丟包模型

DRP環形網絡控制系統在發生故障后，傳感器、控制器以及執行機構之間的數據通信中斷，出現丟包的現象。只有在DRP環形網絡故障恢復后，傳感器、控制器與執行機構之間的數據通信才恢復正常。因此，故障恢復時間的長短直接決定著控制系統丟包的數量，進而影響控制系統穩定性。

如果在冗余切換過程中，即備用鏈路尚未轉換為工作鏈路的情況下，需要進行采樣和控制數據的傳輸，那么將出現丟包現象。假設控制系統采樣周期為T，故障恢復時間為Tw，任意一個交換設備故障的概率為u，傳感器與控制器之間的交換設備數量為n。

進一步假設：q1為上一次和下一次采樣均發生丟包的概率，而q2為上一次和本次采樣均沒有發生丟包的概率。其中q2完全取決于系統采用的交換設備和通信線纜的可靠性。交換設備和通信線纜可靠性高，發生故障的概率小，采樣數據丟失的概率也相應減小。根據T和Tw的關系，分以下兩種情況討論。

3.1 故障時間小于采樣周期

在Tw＜T的情況下，發生故障后，故障在一個T2內恢復。因此不一定會出現丟包。其丟包概率q1＝Tw／T·n·u。進一步得到的上一次和本次采樣均沒有發生丟包的概率為q2＝1－Tw／T·n·u。

3.2 故障時間大于采樣周期

在Tw＞T的情況下，分三種可能，可能出現連續丟包狀態：故障已經恢復，但再次發生故障，必然丟包，其概率為n·u。后兩種情況按照下一個周期不丟包的情況進行分析。如果在下一個宏周期的開始時間（即發包時間）故障仍沒有恢復，則繼續丟包。如果故障已經恢復，則不丟包。故障恢復時間為Tw，可能發生的丟包次數有兩種可能：

故障發生的時間在一個宏周期的區間［0，T－（Tw－T×floor（Tw／T））］內，該次故障一共將導致發生mod（Tw／T）次丟包。因此，綜合考慮上述情況，得到Tw＞T的情況下：

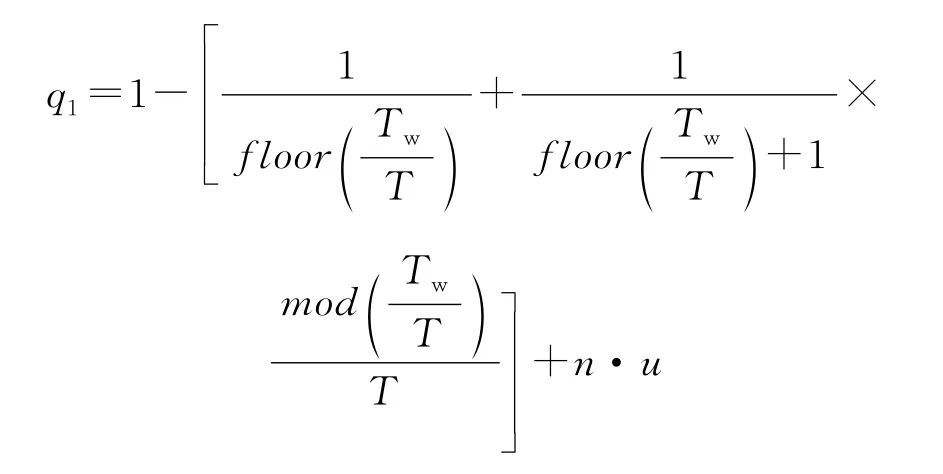
上一次和本次采樣數據均沒有發生丟包的概率為q2＝1－n·u。

4 控制系統穩定性分析

4.1 網絡化控制系統模型

根據建立的DRP環形網絡化控制系統的丟包模型，分析該控制系統的穩定性。在基于DRP環形化網絡的系統中，構建狀態反饋閉環控制系統。假設傳感器采用時鐘驅動方式，傳感器的采樣周期為Th，一般情況下，控制系統的采樣周期T與傳感器的采樣周期Th一致。控制器和執行機構采用事件驅動，系統的被控對象所有狀態均可測，忽略系統中的測量噪聲。

如圖3所示，系統采用比例控制，其離散模型為u（kTh）＝－K x∧（kTh）。其中，u——系統的狀態輸出變量；x——系統的狀態變量；K——比例控制器參數。

令z（k）＝［xT（kTh），x∧T（kTh），u∧T（kTh）］，可得到：z（（k＋1）Th）＝Φiz（kTh）。其中，

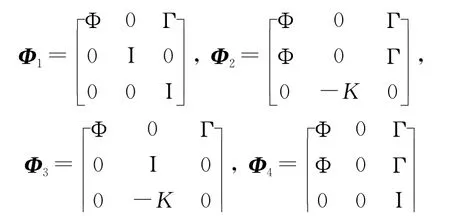
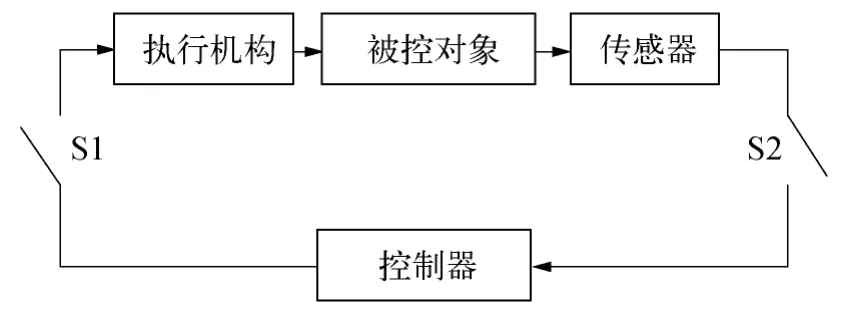
圖3 基于DRP的網絡化控制系統

分別對應4種狀態：i＝1時，S1斷、S2斷；i＝2時，S1通、S2通；i＝3時，S1斷、S2通；i＝4時，S1通、S2斷。

4.2 系統丟包模型下轉移矩陣

任意一個通路的通斷狀態轉移概率矩陣有：傳感器與控制器之間通路的轉移矩陣：

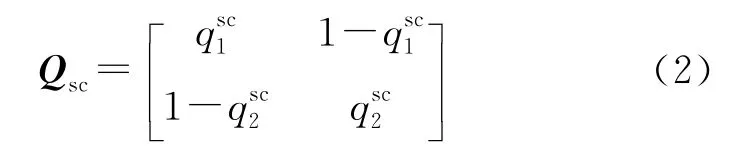
式中：qsc1——傳感器與控制器之間，上一次與下一次采樣均發生丟包的概率；qsc2——上一次和本次采樣數據均沒有發生丟包的概率。

控制器與執行機構之間通路的轉移矩陣：

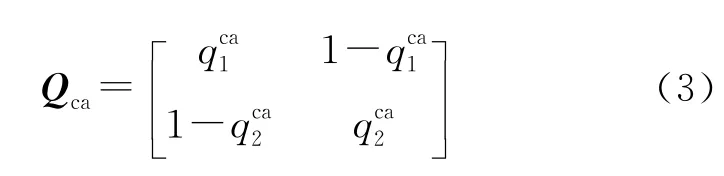
整個控制系統的狀態轉移矩陣：

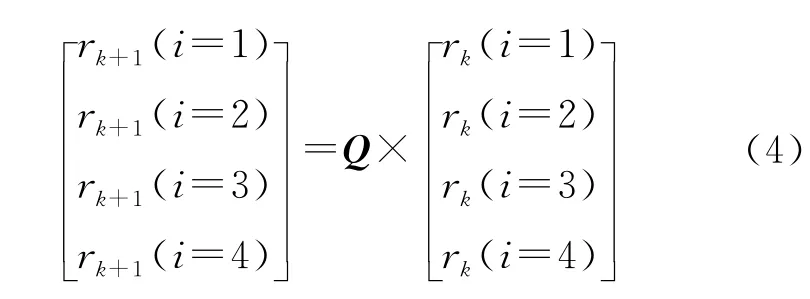
其中i＝1時，S1斷、S2斷；i＝2時，S1通、S2通；i＝3時，S1斷、S2通；i＝4時，S1通、S2斷。

目前，常用的現場總線儀表通常將控制功能集成在現場儀表中。因此，不可能出現CA通路上的“斷”，即。i只可能為2，4，則Q簡化為

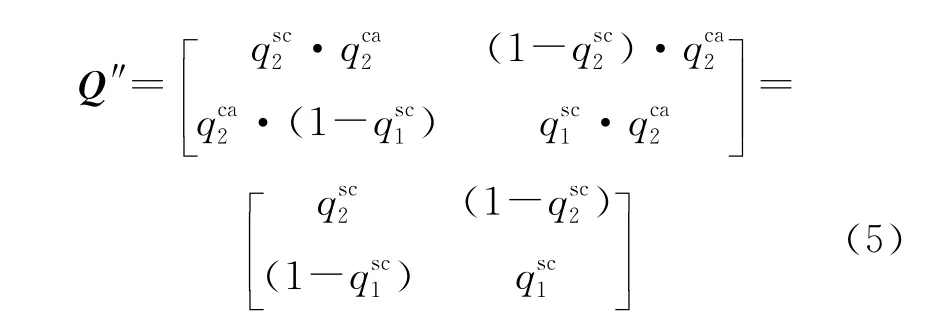
4.3 穩定性分析

根據上述狀態轉移矩陣，分析控制系統穩定性，穩定性判斷矩陣E為

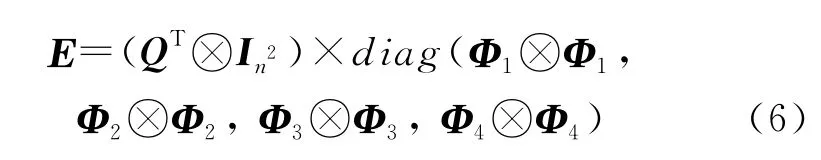
系統的穩定性由E的譜半徑決定。若E的譜半徑小于1，則控制系統穩定。若譜半徑大于1，則被控參數將產生振蕩。

DRP故障丟包模型分為Tw＞T和Tw＜T兩種情況討論。因此，基于DRP的環形網絡化控制系統同樣分兩種情況討論，分別將Tw＞T和Tw＜T情況下的q1和q2丟包模型帶入式（6）得：

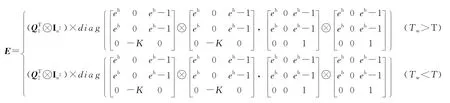
5 仿真驗證

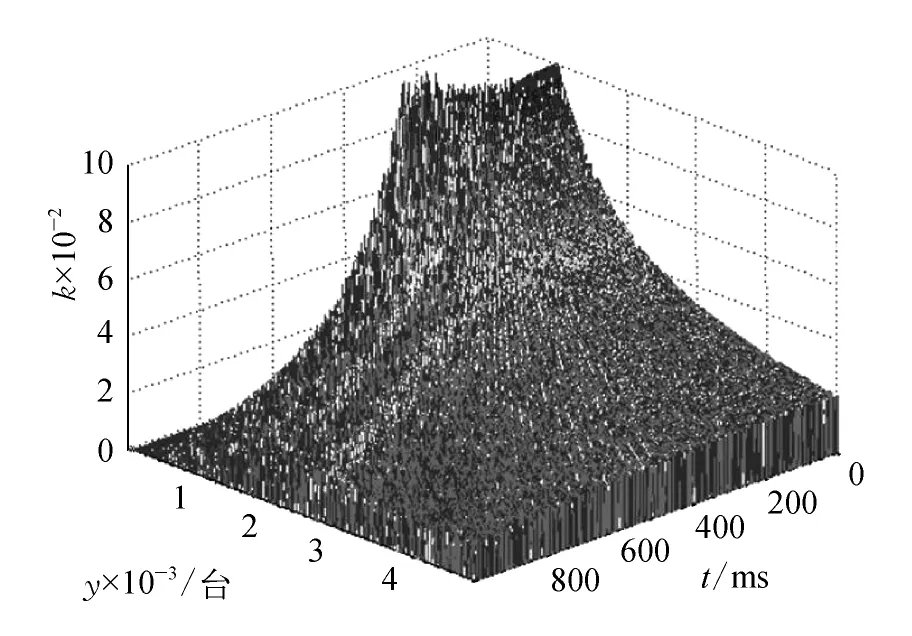
圖4 系統穩定區域

6 結束語

綜上所述，在分析DRP協議的基礎上，得到DRP環形網絡控制系統的穩定性與采樣周期和系統交換設備數量之間的定性關系，為構建環形網絡控制系統提供指導。

另一方面，在環形網絡控制系統中，現有的穩定性條件假設基于故障恢復前后數據傳輸延時不變的情況，存在一部分節點在故障恢復后，由于經過的交換設備數量不同，出現傳輸延時變化的情況，需要在現有模型基礎上經過進一步優化后進行后續研究。

［1］ NILSSON J.Real－time Control Systems with Delays［D］.Lund：Ph.D.Dissertation，Dept.Automatic Control，Lund Institute of Technology，1998.

［2］ ZHANG W，BRANICKY M S，PHILLIPS S M.Stability of Networked Control Systems［J］.Control Systems Magazine，IEEE，2001，21（01）：84－99.

［3］ COSTA L V，FRAGOSO M D，MARQUES R P.Discretetime Markov Jump Linear Systems（Probability and its Applications）［M］.California：Springer，2004.

［4］ HONG S P，KIM Y H，DON S K.A Scheduling Method of Network－based Control Systems［J］.Control Systems Technology，IEEE Transactions on，2002，10（03）：318－330.

［5］ MEIER S，WEIBEL H.IEEE 1588Applied in the Environment of High Availability LANs［C］／／Precision Clock Synchronization for Measurement，Control and Communication.2007：100－104.

［6］ KIM S H.Design and Analysis of High－speed Ring－based Networked Control Systems for Real－time Applications［D］.Berkeley：University of California，2006.

［7］ International Electrotechnical Commission.Industrial Communication Networks High Availability Automation Networks－Part 1：General Concepts and Calculation Methods，IEC 62439－1［M］.Swizerland：International Electrotechnical Commission，2009.

［8］ BYRES E J.Designing Secure Networks for Process Control［C］.Pulp and Paper Industry Technical Conference，1999：63－67.

［9］ International Electrotechnical Commission.Industrial Communication Networks High Availability Automation Networks－Part 6：Distributed Redundancy Protocol（DRP），IEC 62439－1［M］.Swizerland：International Electrotechnical Commission，2009.

［10］ HASSIBI A，BOYD S P.How Control of Asynchronous Dynamical Systems with Rate Constraints on Events［C］.IEEE Conference on Decision and Control，1999.

［11］ SCHEER G W，MOXLEY R E.Digital Communications Improve Contact I／O Reliability［C］.Power Systems Conference：Advanced Metering，Protection，Control，Communication，and Distributed Resources，2006.