倒立擺系統的智能控制算法研究

焦靈俠

（西安工業大學 北方信息工程學院，陜西 西安 710032）

倒立擺系統是一個典型的被控對象，用于檢驗各種控制算法，其本身是一個非線性、強耦合、多變量、自然狀態下不穩定的系統。在控制過程中能有效地反映控制過程中的許多關鍵問題如非線性問題、系統的魯棒性問題、隨動問題、鎮定問題及跟蹤問題等。倒立擺在控制理論研究中是一種較為理想的實驗裝置。倒立擺系統與機器人的站立和行走、通信衛星的實時穩定等有很大的相似性，對倒立擺系統的研究具有重要的理論和實際意義。

1 二級倒立擺系統數學模型的建立

在忽略了空氣阻力和各種摩擦，并認為擺桿為剛體。二級倒立擺[1]示意圖如圖1所示。

圖1 二級倒立擺示意圖Fig.1 Two-stage pendulum schematic diagram

系統的動能：

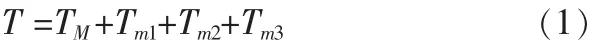
倒立擺參數定義如下：

m1擺桿1的質量 0.05 kg

m2擺桿2的質量 0.13 kg

m3擺桿3的質量 0.236 kg

M小車質量 0.584 kg

g重力加速度 9.8 m/s2

l1擺桿1中心到轉動中心的距離 0.077 5 m

l2擺桿2中心到轉動中心的距離 0.25 m

F作用在系統上的外力 N

θ1擺桿1與豎直方向的夾角 rad

θ2擺桿1與豎直方向的夾角 rad

其中T為系統的動能，V為系統的勢能，L為拉格朗日算子，q為系統的廣義坐標。i=1，2，3…，fi為系統在第i個廣義坐標上的外力。在二級倒立擺系統中，系統的廣義坐標有3個，分別為 x，θ1，θ2。

其中 TM，Tm1，Tm2，Tm3分別為小車的動能， 擺桿 1的動能，擺桿2的動能和質量塊的動能。

擺桿1的動能：Tm1=T′m1+T′m2

其中T′m1，T′m2分別為擺桿1的平動動能和轉動動能。

擺桿2的動能：Tm2=T′m1+T″m2

其中T′m2，T′m2分別為擺桿2的平動動能和轉動動能。

系統的動能為：

系統的勢能為：

由于系統在θ1，θ2廣義坐標下沒有外力作用，所以由拉格朗日方程得：

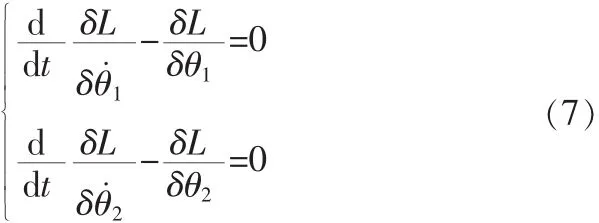
將其在平衡位置附近進行泰勒級數展開，并線性化，代入參數值：

則系統的狀態方程為：

2 倒立擺系統模糊控制器的設計

采用的控制思想是將一個復雜的多輸入/單輸出的模糊控制器，分解成簡單的多輸入/單輸出的模糊控制器[2]。控制器的輸入為控制變量與給定值的偏差和偏差的變化，該方法能夠較嚴格的反映控制系統中輸出變量的動態特性，且控制方法簡單，控制時能及時發現問題，對分別控制小車和擺桿有很大作用。

2.1 模糊控制器的降維

若輸入變量采用常規的控制變量與給定值的偏差和偏差的變化，模糊控制器輸入就有6個，每個變量定義6個模糊子集，模糊控制規則最多有66個，不利于規則的完整制定，將引起“規則爆炸”問題，所以需要對輸入變量進行降維。

本章是用模糊控制和最優控制相結合的方法來實現模糊控制器的降維，使其變成二維模糊控制器[5]。把小車的位移、上擺的擺角、下擺的擺角綜合成一個變量E，將小車的速度、上擺的角速度、下擺的角速度綜合成另一個變量EC，E和EC作為模糊控制器的輸入，電機輸出的控制力u作為輸出，由此可以設計一個二維模糊控制器。

首先利用最優控制中的線性二次型最優調節器控制原理求得最佳狀態反饋控制向量的矩陣，即反饋矩陣K：

系統的狀態向量為：

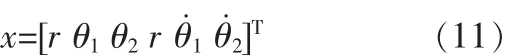
對于二級倒立擺系統，上擺桿即擺桿2的控制難度最大，分別選擇 θ2、θ˙2為控制主元，對應的系數記為：kθ=kθ2，kθ˙=kθ˙2

融合函數的輸出向量記為：

融合函數的輸出方程為：

通過把多個輸入變量降維，得到了綜合誤差E和綜合誤差率EC：

通過信息融合的方法，將二級倒立擺系統的6個輸入變量化為2個輸入變量，減少了模糊控制器的輸入，實現了控制器的降維。

根據二級倒立擺模型的參數，基于MATLAB強大的矩陣運算功能[3]，可以利用命令 K=lqr（A，B，Q，R），得到反饋矩陣K：

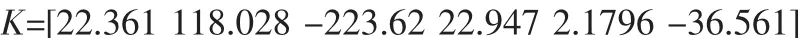
由此得到綜合誤差E和綜合誤差變化率EC。

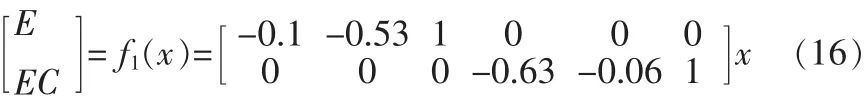
2.2 模糊控制器的設計

1）確定輸入變量和輸出變量

E和EC作為輸入變量，u作為輸出變量

2）E、EC、u 隸屬度函數的設計

圖2 E和EC隸屬度函數曲線Fig.2 Membership function curves of E and EC

圖3 u的隸屬度函數曲線Fig.3 Membership function curves of u

3）模糊推理

采用Mamdani最小運算規則。

4）模糊控制規則

根據輸入/輸出論域上的模糊語言變量劃分NB（負大），NM（負中），NS（負小），ZO（零），PS（正小），PM（正中），PB（正大），設計模糊推理規則如表1所示。

表1 模糊控制規則Tab.1 Rules of fuzzy control

5）解模糊

重心法。

3 仿 真

二級倒立擺系統Simulink仿真模型如圖4所示。

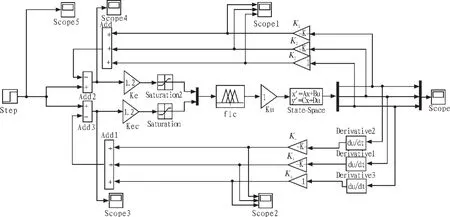
圖4 二級倒立擺系統simulink仿真模型Fig.4 Simulation model of two-stage pendulum

二級倒立擺系統仿真曲線如圖5所示。

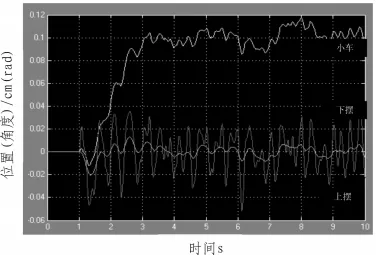
圖5 二級倒立擺系統仿真曲線Fig.5 Simulation curve of two-stage pendulum

4 結 論

通過設計融合函數實現了二級倒立擺模糊控制器的降維，成功解決了模糊“規則爆炸”問題。同時建立了二級倒立擺系統仿真模型，仿真效果較好。

最優控制與模糊控制相結合的方法可以實現二級倒立擺的模糊控制，控制效果良好，結果表明模糊控制能夠使倒立擺系統穩定且具有一定的抗干擾性能。

[1]李洪興，王加銀，苗志宏.模糊控制系統的建模[J].中國科學（A輯）2002，32（9）：772-781.LI Hong-xing，WANG Jia-yin，MIAO Zhi-hong.Modeling of fuzzy control system[J].Science in China （Series A） 2002，32（9）:772-781.

[2]阮治明.二級倒立擺系統的最佳控制[J].兵工自動化，2006，25（1）:60-63.RUAN Zhi-ming.Optimalcontrolofdouble inverted pendulum system[J].Ordnance Industry Automation，2006，25（1）:60-63.

[3]瞿亮.基于MATLAB的控制系統計算機仿真[M].北京:北方交通大學出版社，1998.

[4]席愛民.模糊控制技術[M].西安:西安電子科技大學出版社，2008.

[5]王仲民，孫建軍，岳宏.基于LQR的倒立擺最優控制系統研究[J].工業儀表與自動化裝置，2005（3）:6-9.WANG Zhong-min，SUN Jian-jun，YUE Hong.Based on the LQR optimalcontrolofinverted pendulum system[J].Industrial Instrumentation&Automation，2005（3）:6-9.

[6]唐新宇.倒擺問題的研究及控制器設計[J].天津工業大學，2003，19（4）:65-67.TANG Xin-yu.Stady of the inverted pendulum problem and designing of the controller[J].Tianjin Industrial University，2003，19（4）:65-67.