浮置板軌道系統動力響應分析
耿傳智 宮 寅
(同濟大學鐵道與城市軌道交通研究院,200331,上海∥第一作者,副教授)
城市軌道交通引起的振動噪聲問題已受到廣泛關注,世界各國相繼研究開發了各種減振降噪技術。浮置板軌道結構作為一種特別有效的減振結構,在許多國家和地區已廣泛使用,且在振動隔離、降低噪聲方面取得很大成功。就其長度而言,施工現場澆注的浮置板單塊可以長達數10 m,而工廠預制、現場安裝的浮置板可以短至只有1 m多。在傳統的浮置長板設計中,不同曲線地段的平縱斷面要求是通過調整浮置長板的斷面型式來實現的。但浮置板的斷面、配筋等相關設計都較為復雜,無法進行通用設計,從而影響設計的工作效率。因此,國內外開始采用預制浮置短板、現場拼接的方法。目前,上海、北京、天津、南京等地使用的傳統浮置長板結構的平面尺寸如圖1所示,浮置短板結構的平面尺寸如圖2、3、4所示,浮置板斷面尺寸如圖5所示。本文根據結構動力學原理,運用有限元分析軟件Ansys建立浮置長板-隧道有限元模型、3種長度浮置短板-隧道有限元模型和普通軌道-隧道有限元模型,并運用落軸沖擊法和施加實測輪軌力兩種方法進行計算、分析和對比。所得結果可應用于工程實踐,并可供浮置板軌道的選型和參數優化設計作參考。
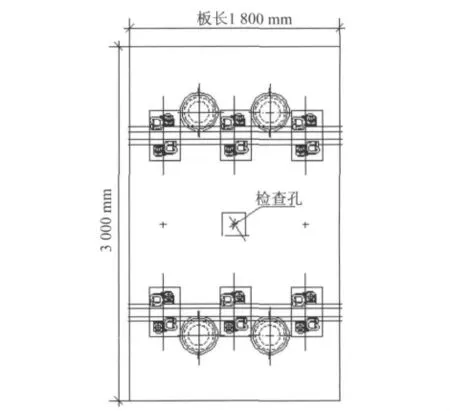
圖2 浮置短板(1.8 m長)平面圖

圖3 浮置短板(3.6 m長)平面圖
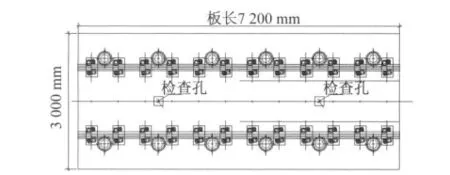
圖4 浮置短板(7.2 m長)平面圖

圖5 浮置板斷面圖
1 浮置板落軸沖擊動力性能有限元分析
當列車車輪通過不平順的軌道時,車輪踏面可能與鋼軌頂面脫離。由于車輛轉向架的一系彈簧處于壓縮狀態,當車輪脫空時,壓縮彈簧將輪對彈向軌面,造成輪軌沖擊。基于該原理,用落軸方法可模擬列車運行時的輪軌間實際沖擊[2]。
1.1 落軸沖擊輪軌接觸單元及有限元控制方程
由于車輪踏面為圓弧面,鋼軌表面為平面,因此落軸沖擊時輪軌間存在瞬時接觸和分開的交錯運動。此計算的重點和難點是如何建立合適的接觸單元,準確模擬輪軌間強烈的瞬態非線性沖擊。因此,需跟蹤接觸面上的點與目標面上的面(或線)的相對位置來確定兩表面間的接觸協調關系。現采用如圖6所示的點面接觸單元模擬輪軌接觸。取踏面表面一節點M 以及鋼軌表面一單元(節點編號為I,J,K,L)組成點面模型[2],其中Q為輪軌接觸點。若節點M侵入鋼軌表面單元,形成一豎直于單元表面的接觸力Fλ,M,作用在M 節點上,相應的反向力Fλ,η被分配到鋼軌單元節點I、J、K、L 上。具體的有限元控制方程見文獻[4]。
1.2 浮置板有限元分析模型及相關參數
傳統的浮置長板的長度l=25m,連續5塊板,每塊板下42個鋼彈簧支座(如圖1);l=1.8m的浮置短板,連續70塊板,每塊板下4個鋼彈簧支座(如圖2);l=3.6m的浮置短板,連續35塊板,每塊板下6個鋼彈簧支座(如圖3);l=7.2m的浮置短板,連續15塊板,每塊板下12個鋼彈簧支座(如圖4);普通軌道長度取125m。鋼軌采用CHN60軌,處理為梁單元;車輪采用塊單元離散,軸重1.2t,根據總重不變原理將車輪處理為等厚度;輪軌間沖擊采用Ansys軟件中Contact點面接觸單元模擬,僅考慮其軸向伸長與壓縮,忽略彎扭剪切與扣件壓力影響;扣件剛度取4×107N/m,阻尼取7.5×104N·s/m;鋼彈簧的剛度取8.5×106N/m,阻尼取1×105N·s/m;浮置板混凝土強度等級為C30,以實體單元模擬。根據總體積不變原理將隧道簡化處理為浮置板板下六面體模型,以實體單元模擬;隧道下均布土彈簧采用彈簧阻尼單元模擬;落軸沖擊發生在相鄰兩扣件間鋼軌中線位置,落軸高度取25mm[4-5]。浮置板-隧道有限元模型如圖7所示,普通軌道-隧道有限元模型如圖8所示,浮置板有限元模擬局部放大見圖9所示。

圖6 輪軌點面接觸單元
2 浮置板落軸沖擊動態響應結果比較
現對不同長度規格的浮置板落軸沖擊動態響應結果比較如下。


2.1 浮置板豎向振動加速度的比較
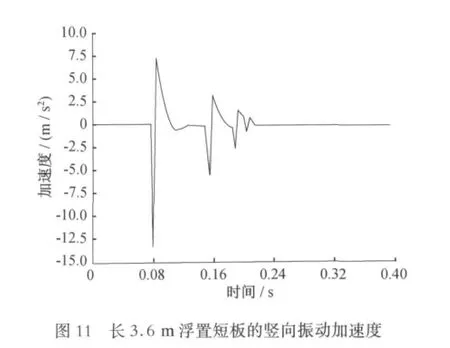
在計算結果中提取落軸位置下方浮置板軌道的豎向加速度,分別在時域內和頻域內對浮置板的豎向加速度進行比較。
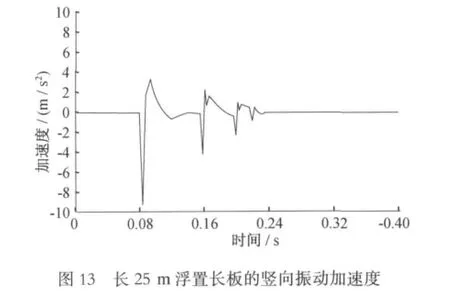
時域內對浮置板豎向加速度的比較見圖10~13所示。
將各模型計算結果的浮置板豎向振動加速度時程曲線進行離散傅里葉變換,得到頻域內對應于各頻率的加速度幅值,再進行1/3倍頻程變換,按規范進行記權。結果如圖14所示。
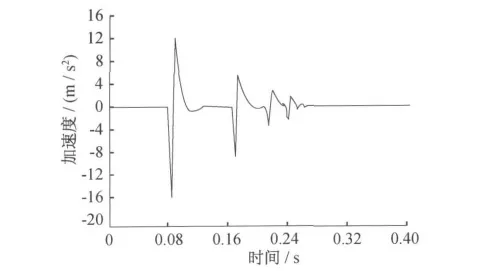
圖10 長1.8m浮置短板的豎向振動加速度
由圖14可知:隨著浮置板長度的增加,浮置板豎向振動加速度幅值減小,但減小幅度較小。


2.2 隧道壁豎向振動加速度的比較
分別在時域內和頻域內對隧道壁的豎向振動加速度進行分析比較。
時域內對隧道壁的豎向加速度分析比較見圖15~19。
將各模型計算結果的隧道壁豎向振動加速度的時程曲線進行離散傅里葉變換,得到頻域內對應于各頻率的加速度幅值,再進行1/3倍頻程變換,按規范進行記權。結果如圖20所示。



由圖20可知:浮置板軌道在20~80Hz內具有良好的隔振效果,可減少振動6~25dB。
3 浮置板在實測輪軌力作用下的動力響應分析
3.1 浮置板分析模型建立與實測輪軌力的施加
浮置板模型參數同上述有限元分析的落軸沖擊模型參數。浮置板-隧道動載荷有限元分析模型如圖21,普通軌道-隧道動載荷有限元分析模型如圖22。將實測輪軌力分別施加在各模型,進行諧響應分析。實測輪軌力時域見圖23,頻域見圖24。




圖21 浮置板-隧道動載荷有限元模型示意圖
3.2 浮置板施加實測輪軌力計算結果分析
對不同長度規格的浮置板施加實測輪軌力的動力響應結果比較如下。

3.2.1 浮置板豎向振動加速度的比較
對時域內浮置板的豎向振動加速度比較見圖25~28所示。
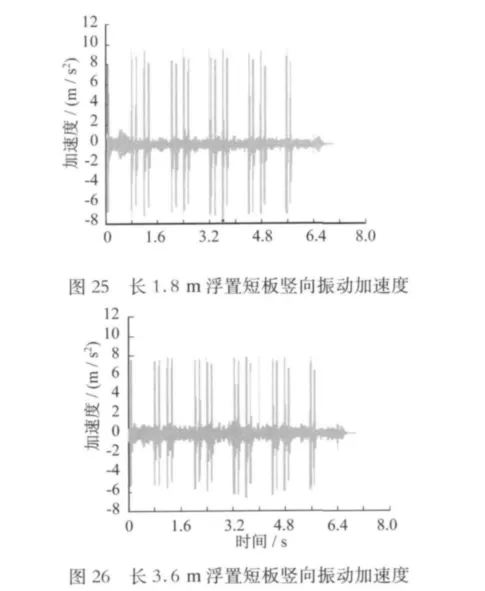

將各模型計算結果的浮置板豎向振動加速度時程曲線進行離散傅里葉變換,得到頻域內對應于各頻率的加速度幅值,再進行1/3倍頻程變換,按規范進行記權。結果如圖29所示。
由圖29可知:隨著浮置板長度的增加,浮置板豎向振動加速度幅值減小,但減小幅度較小。
3.2.2 隧道壁豎向振動加速度的比較
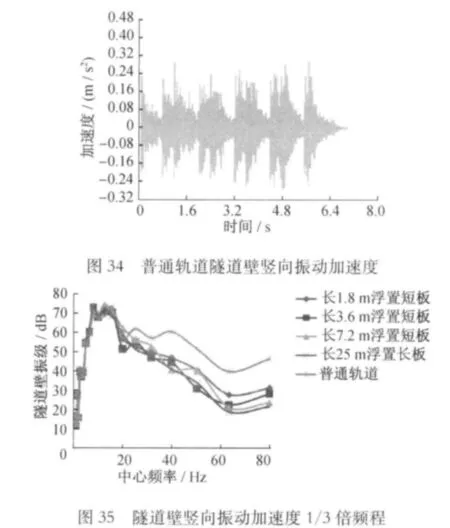
對時域內隧道壁豎向振動加速度的比較見圖30~34所示。

圖29 浮置板豎向振動加速度1/3倍頻程
將各模型計算結果的隧道壁豎向振動加速度的時程曲線進行離散傅里葉變換,得到頻域內對應于各頻率的加速度幅值,再進行1/3倍頻程變換,按規范進行記權。結果見圖35所示。
由圖35分析可知,浮置板軌道在20~80Hz內具有良好的隔振效果,可減少振動6~25dB。

4 結語
對應于現場澆注和預制的浮置板,分別建立浮置長板軌道-隧道、浮置短板軌道-隧道和普通軌道-隧道有限元模型,分析了浮置短板、浮置長板和普通軌道在落軸沖擊作用下和實測輪軌力作用下的動力響應性能,通過分析,兩種方法獲得了一致結論:浮置板軌道在20~80Hz內具有良好的隔振效果,可減少振動6~25dB。浮置板軌道隔振性能主要由其固有頻率決定,并不是由長度決定,只要浮置短板和浮置長板的固有頻率相同,隔振性能基本相同。本文結果可供浮置板軌道的選型和參數優化設計作參考。
[1]王炯,吳天行.浮置板軌道隔振性能研究[J].上海交通大學學報,2007,41(6):1022.
[2]練松良.軌道動力學[M].上海:同濟大學出版社,2003.
[3]Wrigges P,Simo J C,Taylor R L.Penalty and augmented lagrangian formulations for contact problems[C]∥Proceedings of the NUMETA.Swansea:British Technique Press,1985.
[4]朱劍月,耿傳智.高架彈性支撐塊軌道結構落軸沖擊動態響應[J].同濟大學學報:自然科學版,2005,33(12):1621.
[5]耿傳智,王偉鵬.地鐵彈性扣件減振性能的落軸沖擊仿真分析[J].振動與沖擊,2010,29(3):113.
[6]趙錄懷.信號與系統分析[M].北京:高等教育出版社,2003.
[7]耿傳智.地鐵系統振動控制研究[D].上海:同濟大學土木工程學院結構工程與防災研究所,2006.
[8]朱志強.地鐵鋼彈簧浮置板道床存在的缺陷及設計優化[J].城市軌道交通研究,2010(7):50.

