水網航道通過能力的時空消耗計算模型
,,,,
(1.武漢理工大學 航運學院,武漢 430063;2.浙江省港航管理局,杭州 310011 )
關于航道通過能力的計算,國內外在過去的幾十年里曾作過一些研究,并取得了一定的進展[1-2]。我國在航道規劃與建設中,有關航道通過能力的計算方法并無統一的規范公式。大多是借鑒國外有關的經驗公式[3-4],也有研究者提出了考慮船舶交通行為特征的航道通過能力計算模型[5]。綜合國內外已有的研究成果來看,關于航道通過能力的研究主要有兩種學派。一種認為航道通過能力是指單位時間內或特定時段內,能通過航道某區段(或某一地點)的船舶數量[6]。另外一種則認為航道通過能力是指一年內某一區段的航道能通過的最大貨運量,以年通過航道的貨運量(萬t/年)為計算單位[7]。從運力或者運量的角度,用后一種觀點來分析航道的通過能力更能體現實際需求;但從交通組織和交通管理的角度,前一種觀點更能滿足實際工作的需求。目前在計算航道通過能力中更多采用后一種。
由于受到條件和環境的限制,目前我國內河航道的通航標準普遍較低。隨著地區經濟和內河運輸的發展,部分內河航運發達地區的航道阻塞現象己越來越嚴重,特別是在內河航運發達的江蘇、浙江等內河水網地區。因此,從單位時間船舶通過量的角度來研究航道的通過能力,為航道設計、交通管理提供參考具有十分重要的意義。
1 水網航道通過能力計算模型
1.1 水網航道特征分析
我國內河航運發達的江蘇、浙江等內河水網地區,船舶交通流量、相對密度較大,形成了以若干條主干道為中心的網狀航道結構。水網航道干線與支線、干線與干線、支線與支線之間相互交叉連接,而且不同等級的干線航道和不同等級的支線航道之間無論是在船舶的通航尺度還是船舶通航能力等方面都有較大的差異。由于受通航尺度的限制,船舶在航道中航行時基本都是各行其道,保持一種跟馳狀態,與道路交通網中車輛的運行方式有較多的相同之處。但兩者之間也存在一定的差異,例如,對于水網航道來說,船舶只能由主干線駛往支線,不能逆向行駛,而在道路交通網中的車輛行駛相對比較自由。
與道路交通網路類似,對于水網航道,在一定時期內可利用的通航資源是有限的,相對穩定的。船舶交通流中的任何一條船舶都會占用航道設施一定的時間和空間,而其它船舶只能用除此以外的時空資源[8]。船舶在航道中的交通行為,實際上是對水網時空資源的消耗。
鑒于此,可以將路網容量的時空消耗理論應用到水網航道通過能力的計算中。
1.2 理想航道通過能力計算模型
水網航道理想的航道通過能力指航行條件和交通狀況都處于理想的狀態下,單位空間(1 km)或單位時間(1 h)內航道所能服務的最大船舶數,本文簡稱為航道通過能力。
為了簡化研究對象和保證模型的一般性,對計算模型作如下假設:水網航道中行駛的船舶為相同性能、相同技術參數的標準型船舶;并且,當船舶流達到航道最大通過能力時,所有船舶的行駛速度、船頭間距均相同。
1.2.1 一維模型
該模型是以航道有效運營長度與有效運營時間的乘積作為航道的時空總資源,其目標是計算船舶在時空總資源的約束下,單位空間(1 km)內所能服務的最大船舶數。計算模型如下。
(1)
式中:Crd——航道的理想通過能力,艘/km;
C——航道的時空總資源,km·h;
Ciship——船舶在單位時間(1 h)內一次航行的平均時空消耗,(km·h)/艘;
Lr——航道的總長度,km;
T——航道的總有效營運時間,h;
hship——船舶行駛過程中的船頭間距,km;
tship——船舶在1 h內的平均出行時間,h。
1.2.2 二維模型
從水網航道的有效面積的角度出發,提出另一種在時空消耗概念下的航道通過能力——航道所能容納的船舶數。
該模型是以航道的有效運營面積與有效運營時間的乘積作為航道的時空總資源,目的是計算單位時間內整個水網航道所能容納的船舶數,而且它考慮了航道寬度的影響。計算模型如下。
(2)
式中:A——航道的有效面積,m2;
T——航道的總有效營運時間,h;
Ciship——船舶在單位時間內一次航行的平均時空消耗,(m2·h)/艘;
Crd——航道的理想通過能力,艘。
2 計算參數
2.1 一維模型參數
這個模型中需要確定的參數有交通個體行駛過程中的臨界船頭間距hship、航道的總有效營運時間T和交通個體在1 h內的平均出行時間tship。
1)臨界船頭間距的確定。在不考慮船舶追越的情況下,航道理想通過能力狀態是一種穩定的跟馳狀態,跟馳理論是運用動力學方法,研究在無法超船的單向航道上船舶列隊行駛時,后船跟隨前船的行駛狀態的一種理論。船頭間距的基本模型如下:第n+1條船在反應時間tr(后船駕駛員發現狀況到螺旋槳全部停止轉動)內行駛的距離d1,第n+1條船從開始到船舶速度降低到零的停車沖程d2,停車后的最小安全間距d4,第n條船的船長L0以及第n條船從開始到船舶速度降低到零的停車沖程d3,其相對時空關系見圖2。
hship+d3=d1+d2+d4+L0
(3)

圖1 船頭間距模型
假設航道中船舶處于跟馳行駛狀態,第n條船和第n+1條船的停車沖程一樣,即d2=d3。假設反應距離d1=V0tr,代入式(3),可以得到
hship=V0tr+d4+L0
(4)
式中:V0——船舶的臨界速度,km/h;
tr——第n+1條船的反應時間,s;
d4——安全間距,m;
L0——第n條船的船長,m。
船舶在跟馳行駛狀態下,若前船突然停車,則后船需要一定的反應時間才能發現前船的變化從而采取相同的措施。通常情況下,反應時間與船員駕駛水平、駕駛臺水平視距、船舶減速幅度以及航道能見度等有關。根據海員通常做法及良好船藝,此反應時間約為10 s。
最小安全間距d4可參考內河船舶領域三維模型[9]等參考文獻,取單倍船長L0。
2)航道有效營運時間T。在計算時段內,航道有效營運時間T是指航道被有效利用的時間。對于水網航道來說,船舶在特定水域營運過程中,受航道條件限制,有時必須為其它船舶讓路、排隊通過以及限速航行等,這些都影響航道的有效營運時間,將這些綜合因素確定為一個折減系數M1。因此航道的有效營運時間為
T=M1(h)
(5)
3)船舶在單位時間內平均出行時間為t船,這個參數通常希望通過調查得到。
2.2 二維模型參數
1)船舶單位時間內平均時空消耗Ciship,采用變換模型方式計算。
(6)
式中:Ciship——船舶的時空消耗,(h·m2)/艘;
A0——航跡帶寬度,m;
k——船舶交通流密度,艘/km;
t——船舶在單位時間內平均一次出行的時間,h;
lship——船舶在單位時間內平均一次出行的距離,m。
根據《海港總平面設計規范》,航跡帶寬度A0為
A0=n(Lsinγ+B)
(7)
式中:n——船舶漂移倍數;
γ——風、流壓漂角,(°);
B——設計船寬,m。
2)航道的有效運營面積A。保證每一船舶能夠安全航行的航道面積。它是在航道總面積的基礎上,不斷修正的結果。
A=Sc×N1×N2
(8)
式中:Sc——航道的總面積,m2;
N1——航道等級修正系數;
N2——船舶間干擾修正系數。
3)航道的總有效營運時間T。同一維模型。
時空消耗法比較充分考慮了載體與個體的容量平衡關系;概念清晰,形式簡單;易理解,適合較大范圍的水網計算;而且時空消耗法概念下的水網航道通過能力與通行能力的一致性保證了該方法在理論上的正確性;截止目前的研究階段,模型中的大部分變量可以通過調查的方式獲得,無需考慮水網的抽象形式,從而完全回避了網絡的起終點隨機性的難點;而且該方法在處理水網航道的總時空資源和交通個體時空資源時兼顧了動態和靜態兩方面的內容。
3 理想航道通過能力計算實例
3.1 一維模型計算
一維模型計算見表3。

表3 不同等級航道尺度及計算船型
注:數據來源于《京杭運河內河干散貨船標準船型主尺度系列》。
根據實際調查,T=0.8 h,tship=0.8 h,二、三、四、五級航道臨界速度分別為9.13、7.52、7.57、7.61 km/h,計算得到一維模型的航道通過能力,見表4。
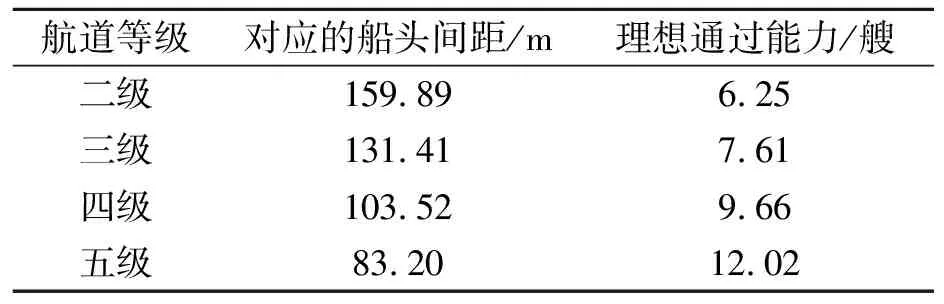
表4 一維模型航道通過能力
由表4可見,本文模型計算出的不同等級的水網航道理想通過能力結果與蘇南運河公式計算結果相近,說明采用本文提出的時空消耗理論一維模型可以計算不同等級航道的理想通過能力。
3.2 二維模型計算
選取京杭運河蘇南段為計算航道,雙向通航,起自鎮江市諫壁口門,止于蘇浙交界的鴨子壩,目前已達到四級航道標準,全長208 km。
A0=1.81×(45sin3°+8.6)=60.72 m
lship=7.57×103×0.8=6 056 m

A=208×1 000×60×0.8=9 984 000 m2

4 實際航道通過能力
通過上述分析,在交通供給與需求處于完全平衡狀態下,當一維模型與二維模型三個參數分別確定以后,水網航道通過能力就確定出來。但是由于各種條件的限制,交通供給與交通需求很難處于平衡狀態,為了更準確地描述水網航道通過能力,還必須考慮外部因素的影響,一般使用修正系數來體現。
1)年通航期系數R1。年通航期系數為全年航行小時數與全年小時數之比,在實際應用中其值[11]按照航道的等級確定,見表5[12]。

表5 天然河流設計最低通航水位保證率
2)水位引起的修正系數R2。通過分析不同水位期的船舶吃水情況,確定枯水期R2取1.0,洪水期和中水期R2應大于 1.0。
3)特殊航道修正系數R3為在其它通航條件不變的情況下,水工建筑修建前后船舶流量的比值。船舶流量的計算通過分析船舶的到達率和船頭間距或船間時距來確定,R3約為0.7~1.0。
4)駕引人員修正系數R4。一般來說R4根據駕引人員的技術熟練程度、遵守交通法規的程度、在本航道或相似條件航道上的駕駛經驗以及駕引人員是否具備正常駕駛行為等來確定,一般為0.9~1.0。對于引航員駕駛的船舶,該值取1.0。
5)船舶航行速度修正系數R5。通過實測船速分析,一般該數值穩定在0.8~0.9 之間。
6)運行船舶不規范修正系數R6。航道中航行的不可能全是標準船舶,需要進行修正,R6 7)船型修正系數R7。大型船舶在航道中占有面積大,當緩速行駛時,將影響航道的通過能力需要進行修正。通過國內多條航道統計分析,該系數一般為0.9~1.0。 通過修正就得出實際航道、交通條件下的通過能力Cr。 Cr=Crd×R1×R2×R3×R4×R5×R6×R7 (9) 但該模型只是計算一段航道的單向船舶通過能力,沒有考慮到雙向通航、交叉航道的情況,也沒有考慮航道等級的差異性、交通分布不均勻等情況;而且模型中的一些參數只能通過調查的方式來獲得,模型中的修正參數太多,參數的確定比較困難,所以從精度上還很難令人滿意。但是時空消耗理論模型是計算航道通過能力最基礎的理論,可以為探索航道通過能力提供參考。 [1] 李 穎.內河航道通過能力研究及其應用[D].南京:河海大學,2006. [2] 長江航道局.航道工程手冊[M].北京:人民交通出版社,2005. [3] 長江航道局.川江航道整治[M].北京:人民交通出版社,1998. [4] 王宏達.內河航道通過量估算[J].水運工程,1998(9):4-6. [5] 文元橋,劉敬賢.港口公共航道船舶通過能力的計算模型研究[J].中國航海,2010,33(2):1-2. [6] 朱 俊,張 瑋. 基于跟馳理論的內河航道通過能力計算模型[J].交通運輸工程學報,2009,9(5):4-5. [7] 卞藝杰.航道通過能力研究[J].水運工程,2000(8):2. [8] 陳春妹,任福田,榮 建.路網容量研究綜述[J].公路交通科技,2002,19(3):2. [9] 徐婷婷.不同安全條件下的航道通過能力研究[D].河海大學,2007. [10] 中華人民共和國交通部.JTJ 211-99海港總平面設 計規范[S].北京:人民交通出版社,1999. [11] 中華人民共和國交通部.GBJ50139-2004內河通航標準[S].北京:人民交通出版社,2004. [12] 劉明俊,萬長征.航道通過能力影響因素的分析[J].船海工程,2008,37(5):6-8.5 結論

