調距槳推進軸系回旋振動計算研究
,,,陳汝
(中國艦船研究設計中心,武漢 430064)
船舶在運行中,由于旋轉質量(主要是螺旋槳)的不平衡力離心力、螺旋槳上的流體激振力以及螺旋槳偏心質量的重力作用,會使軸系產生回旋振動[1-3]。國外一些主要船級社和國內的《鋼質海船入級與建造規范》等都對軸系的回旋振動提出了相應的技術要求。
目前,軸系回旋振動計算的研究主要針對的是定距槳推進軸系[4-6],調距槳軸系具有自身的特點,比如說調距槳質量重造成懸臂效益比定距槳更加明顯,調距槳空心軸內一般充滿槳轂密封油而且布置有油管,調距槳螺轉動慣量隨著螺距的變化發生改變等,因此有必要對調距槳軸系回旋振動計算進行分析。
1 回旋振動計算的傳遞矩陣法
軸系回旋振動頻率的計算采用傳遞矩陣法,計算當量模型采用集總參數元件-分布參數元件混合模型。
軸系回旋振動當量模型,從螺旋槳端起,到柴油機飛輪或傳動齒輪箱中的大齒輪首端或彈性聯軸節從動部分為止[7]。
采用集總參數元件-分布參數元件混合系統,將研究對象的軸系簡化為三類元件:螺旋槳簡化為勻質剛性圓盤元件;中間軸、艉軸和螺旋槳軸簡化為勻質軸段元件;各軸承簡化為支承元件。建立的振動當量模型見圖1。

8-艉軸架軸承;14-艉軸管軸承;20-中間軸承;31、35-齒輪箱支承軸承
圖1回旋振動計算當量模型
軸系基本參數見表1。

表1 軸系基本參數
通過當量模型的建立,將軸系由復雜的彈性系統分解為一系列慣性元件和彈性元件連接而成的簡單模型。按照一般結構靜力學的線性理論,任兩個相鄰端面的狀態矢量通過一個線性變換聯系著, 也就是相鄰兩端面的狀態矢量用一個矩陣相互聯系著,變換矩陣把狀態矢量從此端面遷移或傳遞至彼端面。
傳遞矩陣法就是將這些元件的結合面作為計算端面,列出元件端面處的狀態矢量, 然后, 利用彈性系統各部分之間的傳遞關系, 列出傳遞矩陣, 最后,將各個元件逐個地連接起來,連續相乘得到系統的傳遞矩陣并求解。
2 調距槳軸系回旋振動計算分析
2.1 螺距變化的影響
螺旋槳在水中運轉振動時,有一部分振動能量傳遞給水。在振動計算時,將這部分能量用參與振動的附連水質量及轉動慣量計入,并把它加到螺旋槳的質量和轉動慣量上。
隨著螺距變化,調距槳附連水系數發生變化,螺距越小,附連水系數也越小,調距槳轉動慣量越小,從而導致固有頻率上升。
目前考慮附連水效應時,通常是直接給螺旋槳質量和轉動慣量乘以給定的附連水系數,但是,采用固定的附連水系數沒有考慮到螺旋槳幾何尺寸、結構參數等影響,計算結果往往誤差較大,而且對于調距槳,由于螺距的變化,導致附連水系數并不相同。因此本文采用二維振動翼理論求得的附連水質量Δm、附連水極轉動慣量ΔJp和附連水徑向轉動慣量ΔJd。
該方法將螺旋槳葉片的展開近似看為橢圓,具有一定的精度,而且公式簡單,具有工程應用價值。
(1)
(2)
(3)
式中:ρ——海水密度,kg/m3;
Dp——螺旋槳直徑,m;
Zp——螺旋槳葉片數;


根據上述方法,得到該調距槳螺距變化時調距槳附連水系數見表2。

表2 附連水系數計算表
注:螺距比1.00代表滿螺距;0代表零螺距。
從表2見,隨著螺距的降低,質量附連水系數和轉動極轉動慣量附連水系數都隨之降低,由于附連水徑向轉動慣量與螺距比無關,因此徑向轉動慣量附連水系數基本不變。
根據以上計算結果,得到軸系回旋振動固有頻率隨螺距變化的結果,見圖2。

圖2 頻率隨螺距變化示意
結果表明,隨著螺距的降低,軸系回旋振動固有頻率明顯上升,零螺距時相對滿螺距時頻率變化~5%,因此在調距槳軸系回旋振動計算時,應該對滿螺距和零螺距分別進行校核。
2.2 軸承支承點位置的影響
回旋振動計算分析中,一般將軸承簡化為單點支承。對于中間軸承、艉軸管軸承等,支承反力可以認為是分布均勻的,支承點近似假定在軸承中央位置。但對于艉軸架軸承,由于受懸臂端螺旋槳的作用,軸承支反力沿軸承長度分布很不均勻,支承點偏向船艉。螺旋槳越重,支承點偏離軸承中央位置就越多。有關機構給出了艉軸承支承點選取的近似選取范圍,見表3。

表3 艉軸架軸承支承點位置
注:L-艉軸架軸承襯長度;D-軸徑。
在支點位置取距軸承襯后端(1/7~1/2)L長度范圍時,計算得到的回旋振動固有頻率見圖3。
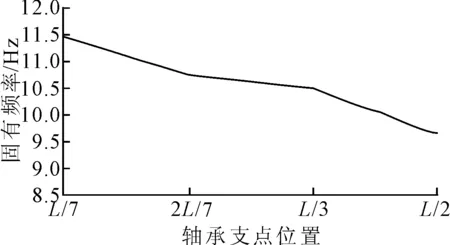
圖3 艉軸架軸承支點位置對頻率的影響曲線
結果表明,艉軸架軸承支點位置對計算頻率影響較大,相差超過15%,因此本文針對艉軸架軸承建立考慮油膜特性的非線性模型,并采用動態校中方法合理確定軸承支點位置[8-10]。
模型主要基于流體潤滑動力學理論,描述徑向滑動軸承油膜運動的雷諾方程為
(4)
對方程進行無量綱化,令

式中:h——油膜厚度;
p——油膜壓力;
x——軸徑向長度;
z——軸向長度;
U——線速度;
ω——角速度;
Rb——軸承半徑;
Rj——軸頸半徑:
L——軸承長度。
得到雷諾方程的無量綱形式如下。
(5)
由于螺旋槳懸臂作用的影響,軸系中心線呈曲線,與軸承中心線有一定的夾角。假設軸承中心截面的偏心距為e0,得到軸承任意位置的偏心距、偏離角和油膜厚度為
(6)
(7)
h=Rbψ[1+εcos (θ-φ)]
(8)
式中:e′——軸頸軸線在軸承中截面的投影長度;
α——投影夾角;
φ0——軸承中截面上的偏位角;
ε——偏心率;
θ——油膜角度。
根據以上方法得到求得支承軸油膜壓力分布,進一步積分可得到垂直方向合力和力矩為
(9)
(10)
軸承支反力位置為
z=M/F
(11)
軸承支反力位置通過迭代方法得出,首先假定軸承支點位置為z0,計算得到軸承油膜壓力分布,進而計算得到軸承支點位置z,若其與初始假定值相差很小,則認為其為軸承支點位置,否則對軸承支點位置進行修正后重新進行計算,如此反復迭代計算得到軸承支點位置距軸承襯后端約0.23L,計算流程見圖4。

圖4 支點位置計算流程
2.3 調距槳軸內油的影響
調距槳推進軸系的中空軸內,一般充滿槳轂密封用的液壓油,會對軸段的彎曲產生影響,進而影響軸系回旋振動特性。
傳遞矩陣法中,中間軸、艉軸和螺旋槳軸簡化為勻質軸段元件,本文將軸內液壓油的單位長度重量加到軸段材料密度中,在不影響算法的情況下,分析軸內液壓油對軸系回旋振動特性的影響。
根據以上方法,該型船軸段密度增加約2%,計算得到軸系回旋振動固有頻率增加不到1%,因此在計算調距槳推進軸系時,可以忽略軸內液壓油對其的影響。
3 結論
1)調距槳螺距變化對回旋振動計算結果有較大影響,隨著螺距的降低,軸系回旋振動固有頻率明顯上升,因此在分析調距槳軸系回旋振動特性時,應該對滿螺距和零螺距分別進行計算;
2)艉軸架軸承支承點的選取,對計算結果影響很大,特別是對于白合金軸承,國內外規范支承點的選取范圍很大,可通過軸系合理校中計算得出支承點位置,以保證計算精度;
3)軸系中空軸段內密封油對軸系回旋振動特性基本沒有影響,在計算中可以不予考慮。
[1] 譚祖盛,陳川艾,郭賢民.高速船推進軸系回旋振動影響因素及特點探析[J].船舶工程,1999(3):32-34.
[2] 梁向東. 軸系的回旋運動對船舶噪聲的影響[J].噪聲與振動控制,2007(2):69-70.
[3] 何靈聰,黃次浩,朱從喬,等.軸系回旋振動的計算機測試系統研究[J].海軍工程學院學報,1997(3):104-109.
[4] 劉 剛,吳 煒,饒春曉,等.基于傳遞矩陣法的船舶軸系回旋振動計算研究[J].中國艦船研究,2010(1):60-63.
[5] 陳錫恩,高 景.船舶軸系回旋振動計算及其參數研究[J].船海工程,2001,30(5):8-11.
[6] 周瑞平.基于VB的船舶軸系回旋振動計算軟件[J].造船技術,1999(3):30-33.
[7] 陳之炎. 船舶推進軸系振動[M].上海:上海交通大學出版社,1987.
[8] CABRERA D L.WOOLLEY N H.Film pressure distribution in water-lubricat I ed rubber journal bearings[J]. Proceedings of the MECH E Part J Journal of Engineering Tribology, 2005(2):125-132.
[9] 耿厚才.饒柱石,崔 升.船舶軸系油膜計算與軸承反力分析[J].船舶力學,2004 (5):120-124.
[10] 周瑞平,李冰融,李增光.船舶推進軸系校中計算中軸承油膜的影響分析[J].船海工程,2005,34(4):64-67.

