Q345B鋼動態再結晶動力學模型研究

楊 靜，徐 光，韓 斌，補叢華，鄒 航

（1.武漢科技大學鋼鐵冶金及資源利用省部共建教育部重點實驗室，湖北武漢，430081；2.武漢鋼鐵（集團）公司研究院，湖北武漢，430080）

Q345B鋼是一種普通的低合金高強度鋼，因其良好的綜合力學性能、低溫性能和焊接性能，在機械制造和工程建設中得到廣泛應用。隨著對Q345B鋼軋制工藝研究的不斷深入，以及數值模擬技術在軋制工藝和軋件質量控制等方面的應用，建立適當的Q345B鋼熱變形動態再結晶動力學模型是一項具有實際意義的工作。

目前關于金屬熱加工過程中動態再結晶的報道很多[1－4]，但針對Q345B鋼動態再結晶的研究較少。文獻[5]研究了CSP工藝條件下Q345B鋼的動態再結晶，該文進行了單道次變形實驗，給出了Zener－Hollomon參數方程，但沒有建立再結晶體積分數模型。文獻[6]研究了Q345B微合金鋼的高溫動態再結晶，但沒有討論動力學模型。動態再結晶動力學模型有Epsilon－S／Epsilon－C模型[7－8]、Epsilon－P模型[9－10]和Epsilon－S模型，但現有文獻都沒有驗證哪種模型是最優模型。本文在Gleeble 1500熱模擬實驗機上進行Q345B鋼單道次壓縮變形實驗，采用應變硬化率方法得到穩態應變，并應用Johnson－Mehl－Avrami（JMA）方程法建立再結晶體積分數模型。根據單道次壓縮實驗結果建立了Zener－Hollomon參數方程，給出動態再結晶狀態圖，回歸出3種再結晶體積分數計算模型，并進行比較分析，得到最優的Q345B鋼再結晶動力學模型，以期為碳錳鋼組織和性能預報軟件的開發提供冶金物理學模型。

1 實驗

試樣取自某熱軋帶鋼廠生產的Q345板坯，其化學成分如表1所示。將試樣加工成φ8 mm×18 mm的圓柱體，按圖1所示工藝流程在Gleeble 1500熱模擬機上進行單道次壓縮試驗，記錄變形過程中的應力－應變數據。

表1 試樣的化學成分（wB／%）Table 1 Chemical compositions of the sample

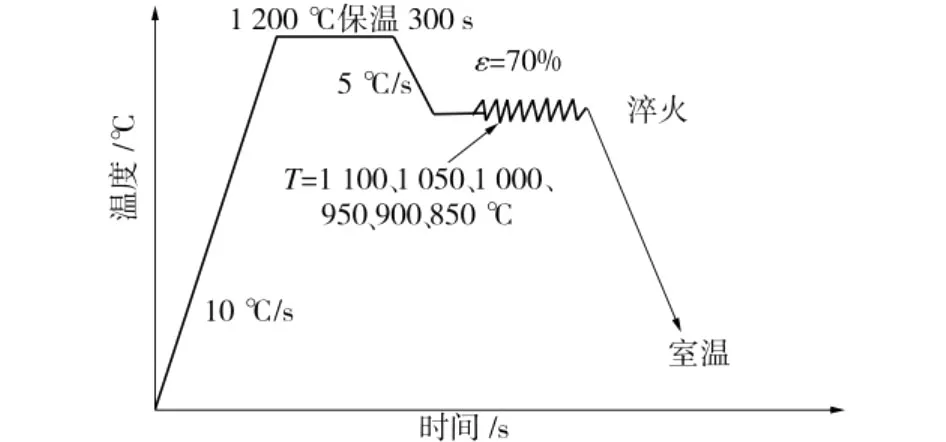
圖1 單道次壓縮試驗工藝圖Fig.1 Schematic illustration of single－pass compression experiment

2 結果與分析

2.1 真應力－真應變曲線

圖2所示為Q345B鋼高溫單道次壓縮變形真應力－真應變的部分曲線。從圖2（a）中可以看出，在相同的變形溫度下，隨著應變速率的減小，應力也隨之減小；在1 100℃、3種不同變形速率下，試樣都發生了明顯的動態再結晶現象。從圖2（b）中可以看出，變形速率為1 s－1時，在不同的變形溫度下，試樣也發生了動態再結晶，而且隨著變形溫度的升高，應力峰值向真應變減小的方向移動，表明動態再結晶更易發生。

金屬的高溫變形是一個熱激活過程，熱激活能隨著變形溫度的升高而增大，使位錯具有足夠的活動能力，克服釘扎作用而運動。同時，在升溫過程中，由加工硬化造成的位錯密度會有所下降，宏觀上表現為應力峰值下降。熱激活決定了動態再結晶的過程，所以隨著溫度的升高，金屬再結晶形核率增加，促進動態再結晶的發生。

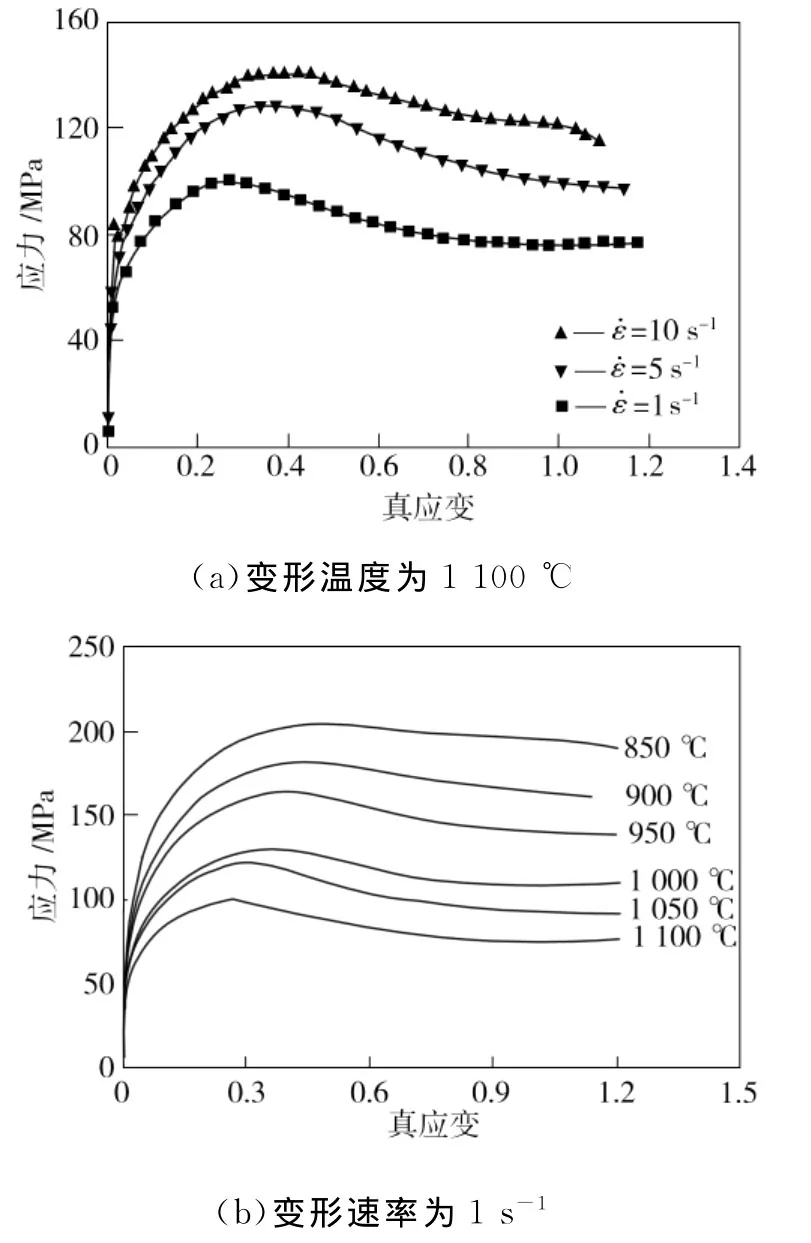
圖2 Q345B鋼的真應力－真應變曲線Fig.2 True stress－true train curves of Q345B steel

2.2 模型特征值確定

建立再結晶動力學模型需要3個變形特征值：臨界應變εc、峰值應變εp和穩態應變εs。峰值應變εp可由應力應變曲線上對應的峰值應力得到。臨界應變本文取εc＝0.8εp。對于穩態應變εs，一般通過應力－應變曲線或加工硬化率θ與應變ε的關系曲線來確定[12]，通過應力－應變曲線上的穩態段來確定穩態應力εs帶有主觀因素，有一定的誤差，本文采用應變硬化率方法來確定εs的值。

應變硬化率定義為

式中：Δσ為真應力增量；Δε為真應變增量。

根據熱模擬實驗數據可作出1 100℃下變形速率為1 s－1時試樣加工硬化率θ與應變ε的關系曲線，如圖3所示。從圖3中可以看出，隨著應變ε的增大，加工硬化率θ先逐漸減小至小于0的一個極小值；ε繼續增大，若θ又增大到0且維持在0值，則表明此時發生的動態再結晶為連續型的，若θ又在0值上下波動，則表明動態再結晶為周期型的。在動態再結晶模型中，把θ第一次恢復到0值時的應變作為穩態應變εs，由此可以得到不同變形條件下的穩態應變εs。

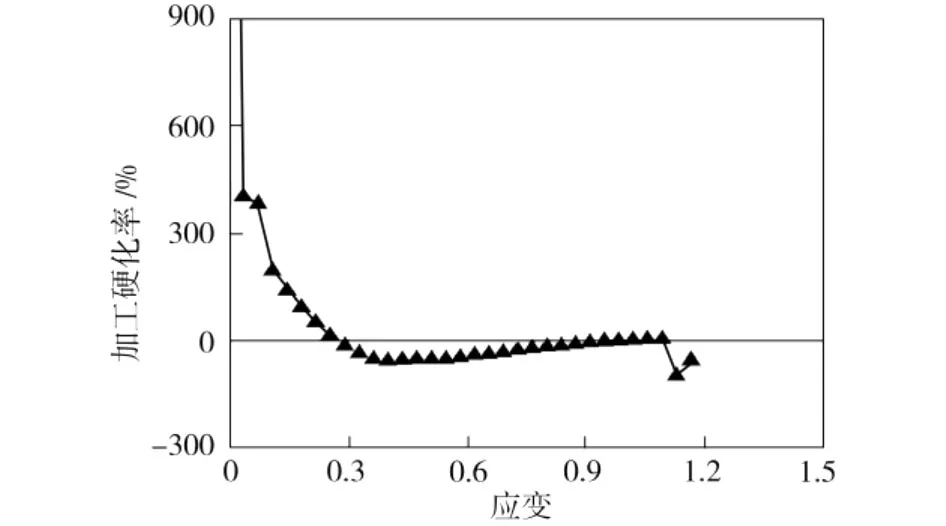
圖3 Q345B鋼的加工硬化率－應變曲線Fig.3 Workhardening rate－strain curve of Q345B steel

3 動態再結晶動力學模型

3.1 Z參數方程和再結晶狀態圖

動態再結晶是一個熱激活過程，熱變形激活能Qdef由下式[13]計算：

式中：R為常數，R＝8.314 4 J／（mol·K）；n、b為根據實驗數據回歸的參數。

根據試驗數據，可以作出1 000／（273＋T）與ln[sinh（ασp）]（α為常數，α＝0.012）的關系曲線（見圖4），回歸所得其平均斜率即為b值；作出不同溫度下ln[sinh（ασp）]與ln關系曲線（見圖5），回歸所得斜率倒數的平均值即為n值。由圖4、圖5回歸可得b＝8.285，n＝4.845，代入式（2）可得Qdef＝Rnb＝333.75 kJ／mol。

Zener－Hollomon（Z－H）參數為[12]

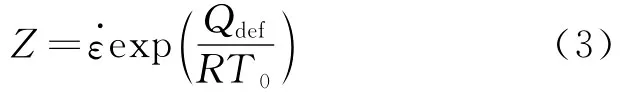
式中：T0為變形溫度，K。

根據Z－H參數方程，可以計算得到不同條件下的Z參數，由此可以得到不同變形條件下試樣的再結晶狀態圖，如圖6所示。

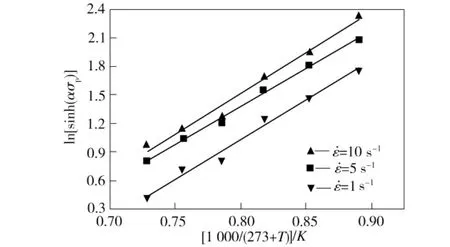
圖4 ln[sinh（ασp）]與1 000／（273＋T）的關系曲線Fig.4 Relation between ln[sinh（ασp）]and 1 000／（273＋T）

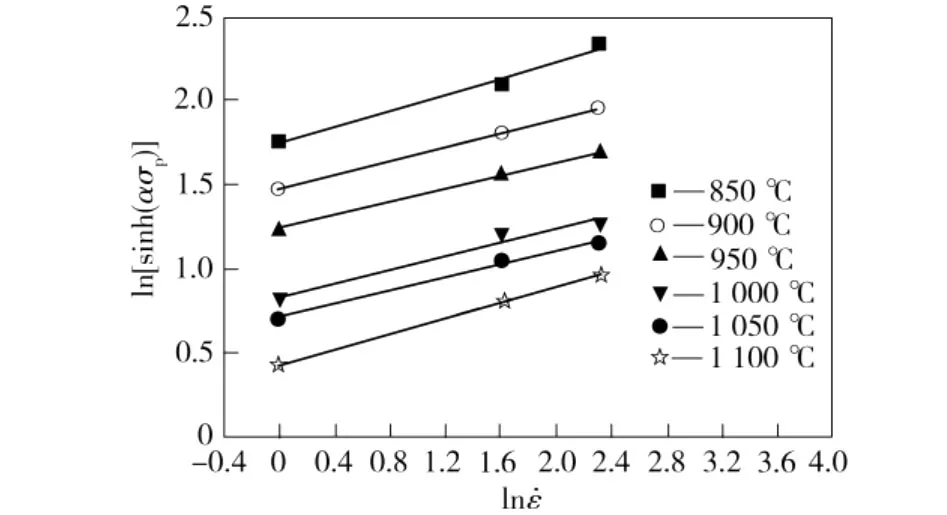
圖5 ln[sinh（ασp）]與ln的關系曲線Fig.5 Relation between ln[sinh（ασp）]and ln

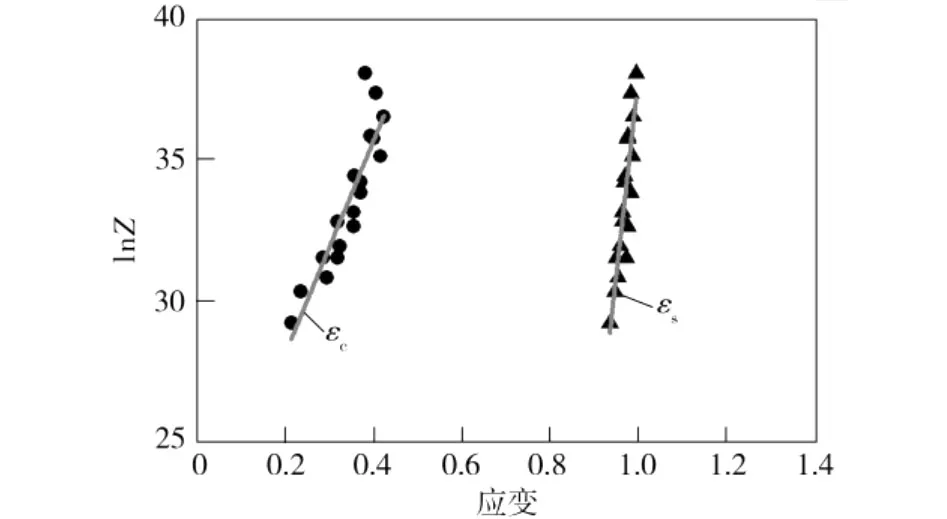
圖6 Q345B動態再結晶狀態圖Fig.6 Status diagram of dynamic recrystallization of Q345B steel

3.2 實測再結晶體積分數

動態再結晶體積分數的計算方法有金相法[14]、σ－ε曲線法[15－16]和Johnson－Mehl－Avrami（JMA）方程法[17－18]。金相法即把發生不同程度動態再結晶的試樣從高溫淬火到室溫，通過觀察其顯微組織中再結晶晶粒的多少來確定高溫變形狀態下試樣的再結晶體積分數，這種方法實驗復雜，而且在觀察顯微組織時，由于再結晶晶粒和未再結晶晶粒很難區別，所得結果精度不高。σ－ε曲線法認為變形組織的外推流變應力是σd，再結晶組織的流變應力是σs，則熱變形發生動態再結晶過程中流變應力為σ時對應的動態再結晶體積分數為Xd＝（σd－σ）／（σd－σs），在不同的變形條件下，用外推法很難準確確定變形組織的流變應力σd，且目前采用這種方法的文獻也沒有給出具體的流變應力σd的確定方法。Johnson－Mehl－Avrami（JMA）方程法應用十分廣泛，本文也采用該方法來確定動態再結晶的體積分數fdyn。

JMA方程為

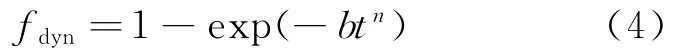
式（4）中n和b在不同的變形條件下不是常數，而是與變形參數有關的變量，因此，JMA方程可以改寫為：

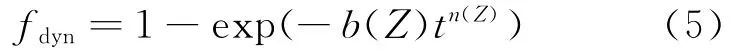
式中：fdyn為動態再結晶體積分數，%；b（Z）和n（Z）為變形參數Z的函數。

假定達到臨界應變εc時試樣的再結晶體積分數為0.5%，穩態應變εs對應的再結晶體積分數為99%，則式（5）可改寫為

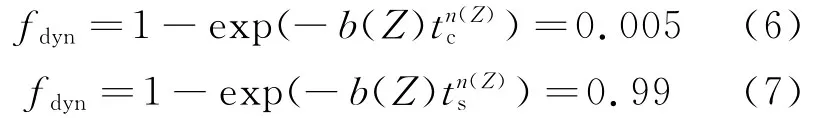
由式（6）、式（7）可得：

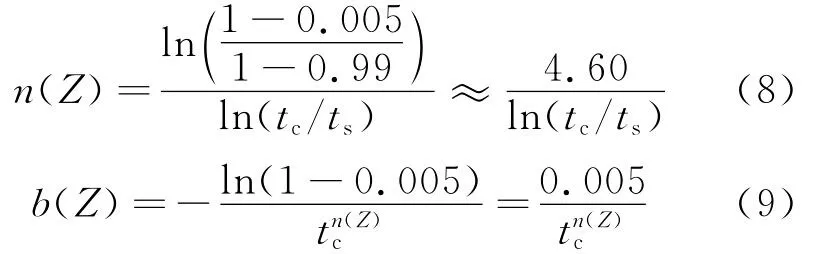
由式（8）和式（9）得到不同變形條件時n（Z）和b（Z）的值，代入式（5）可得到動態再結晶動力學方程。然后，可由此方程計算得到不同變形條件下試樣的動態再結晶體積分數。

3.3 動態再結晶體動力學模型

一般認為，將式（4）轉變為應變的函數，即可得到再結晶體積分數預報模型。目前廣泛采用的動態再結晶體積分數模型有兩種，即Epsilon－S／Epsilon－C模型：

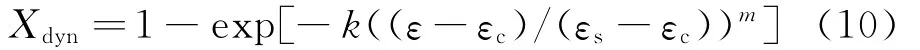
和Epsilon－P模型：

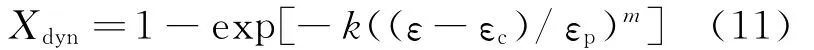
筆者提出新的動態再結晶體積分數模型——Epsilon－S模型：

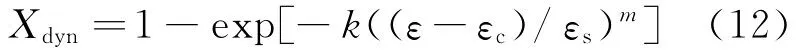
上述3種模型描述的都是S型曲線動力學規律，符合金屬再結晶的變化規律。分析這3種模型可知，其分子項是相同的，不同的是分母項。Epsilon－S／Epsilon－C模型考慮了動態再結晶的開始點和完成點，考慮了動態再結晶的整個過程，精度應該最高；Epsilon－P模型只考慮了達到峰值應力之前的動態再結晶過程，忽略了峰值應力和穩態應力之間很大一部分的再結晶過程，所以模型誤差應該最大；Epsilon－S模型中將變形開始到臨界應力之間的未再結晶過程也考慮在內，但是臨界應力之前的形變在總變形中所占比例較小，所以造成的誤差不會很大，模型精度應該居另二者之間。

為了對比分析這3種模型的精度，用實驗得到的變形特征值數據分別進行回歸得到相應的Q345B鋼的動態軟化率動力學模型：EpsilonS／EpsilonC模型：

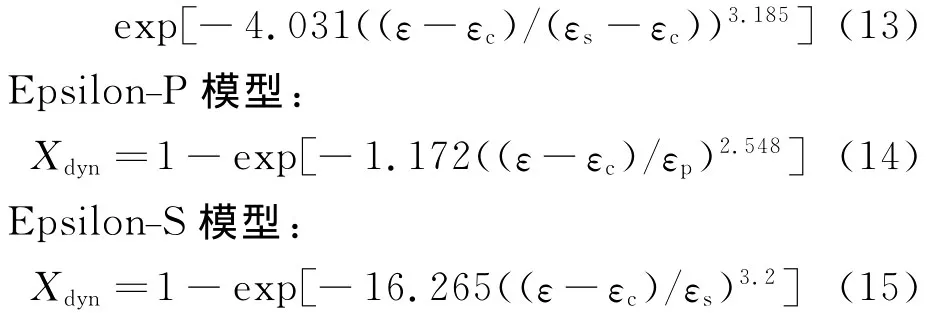
由SPSS軟件計算可得，3種模型的相關系數分別為R1＝0.991、R2＝0.933、R3＝0.990。將回歸得到的模型用實驗實測值和模型預報值進行對比，結果如圖7所示。從圖7中可以看出，Epsilon－S／Epsilon－C模型精度最高，Epsilon－S模型精度與之相當，Epsilon－P模型精度最差，這與前面的分析相吻合。

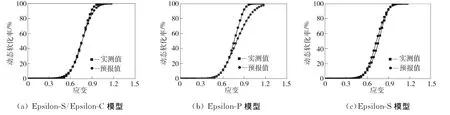
圖7 再結晶體積分數的實測值和預報值Fig.7 Comparison between measured and predicted DXR values

4 結論

（1）Q345B的熱變形激活能為333.75 kJ／mol。

（2）從再結晶冶金物理學意義角度考慮，動態再結晶力學模型Epsilon－S／Epsilon－C、Epsilon－P和Epsilon－S中，Epsilon－S／Epsilon－C模型具有最高的精度，筆者提出的動態再結晶體積分數模型Epsilon－S的精度次之。

[1] 魏潔，唐廣波，劉正東.碳錳鋼熱變形行為及動態再結晶模型[J].鋼鐵研究學報，2008，20（3）：31－35.

[2] 曹杰，唐廣波，閻軍，等.C－Mn鋼單道次壓縮動態再結晶實驗研究與數值模擬[J].安徽工業大學學報，2010，27（3）：266－268.

[3] 周曉光，劉振宇，吳迪，等.FTSR熱軋含Nb鋼動態再結晶數學模型中參數的確定[J].金屬學報，2008，44（10）：1 188－1 192.

[4] 劉鵬飛，劉東，羅子健，等.GH761合金的熱變形行為與動態再結晶模型[J].稀有金屬材料與工程，2009，38（2）：275－280.

[5] 何建中，劉雅正，史秉華，等.Q345含Nb低碳鋼CSP軋制時動態再結晶的研究[J].特殊鋼，2005，26（3）：10－13.

[6] 宿成，董方，席玉軍，等.Q345B微合金鋼的高溫變形行為[J].內蒙古科技大學學報，2010，29（4）：319－322.

[7] 吳瑞恒，朱洪濤，張鴻冰，等.0.95C－18W－4Cr－1V高速鋼動態再結晶的數學模型[J].上海交通大學學報，2001，35（3）：339－341.

[8] 余馳斌，葉傳龍，趙剛，等.Nb－Ti鋼高溫變形時動態再結晶行為及模型探討[J].武漢科技大學學報：自然科學版，2003，26（4）：334－336.

[9] 張春玲，孫睿璇，蔡大勇，等.Cu－P－Cr－Ni－Mo耐候鋼高溫變形奧氏體的動態再結晶[J].特殊鋼，2010，31（4）：43－45.

[10] 王曉明，洪惠平，王孟，等.37Mn5鋼高溫變形抗力模型及動態再結晶動力學模型研究[J].武漢科技大學學報，2010，33（5）：497－500.

[11] Devadas C，Samarasekera I V，Hawbolt E B.The thermal and metallurgical state of steel strip during hot rolling：PartⅢ.microstructural evolution[J].Metallurgical and Materials Transactions A，1991，22A：335－349.

[12] 徐光，徐楚韶.Ti－IF鋼動態再結晶模型[J].特殊鋼，2006，27（6）：13－14.

[13] 沈丙振，方能煒，沈厚發，等.低碳鋼奧氏體再結晶模型的建立[J].材料科學與工藝，2005，13（5）：516－520.

[14] 關云，李平和，陳慶豐.變形溫度對ULCB鋼動態再結晶的影響[J].武鋼技術，2007，45（5）：15－18.

[15] 程曉茹，李虎興，葛懋琦，等.管線鋼X65高溫變形動態再結晶研究[J].金屬學報，1997，33（12）：1 275－1 280.

[16] 張毅，劉平，田保紅，等.Cu－Ni－Si－Ag合金動態再結晶數學模型[J].特種鑄造及有色合金，2010，30（9）：787－790.

[17] 徐光，張丕軍.金屬低溫變形與技術[M].北京：冶金工業出版社，2007：157.

[18] Kirihata A，Siciliano F，Maccagno T M，et al.Mathematical modelling of mean flow stress during the hot strip rolling of multiply－alloyed medium carbon steels[J].ISIJ International，1998，38（2）：187－195.