一道 “復(fù)合場”試題的三種解法
張會麗
(登封市第一高級中學(xué) 河南 鄭州 452470 )
帶電體在復(fù)合場中的運動是高中物理電學(xué)部分的重點,也是難點,當然也是高考的重要考點,在高中物理新課程中也必然占有重要的份量.學(xué)生要想靈活應(yīng)用這一部分的知識,就必須對帶電粒子單獨在重力場、電場和磁場中運動的規(guī)律準確地掌握,對力學(xué)的牛頓運動定律、動能定理、能量守恒定律、動量定理等規(guī)律清楚地認識.下面對一道關(guān)于復(fù)合場的高考題中三種解法進行比較,旨在讓讀者對帶電粒子在復(fù)合場中的運動認識得更深刻,理解得更透徹.
【例】在場強為B的水平勻強磁場中,一質(zhì)量為m,帶正電q的小球,在O點靜止釋放,小球的運動曲線如圖1所示.已知此曲線在最低點的曲率半徑為該點到x軸距離的2倍,重力加速度為g.求:

圖1
(1)小球運動到任意位置P(x,y)的速率v;
(2)小球在運動過程中第一次下降的最大距離ym;

解法1:常規(guī)解法
(1)由于小球在下落過程中,洛倫茲力總與速度方向垂直,不做功,只有重力做功,所以
(2)小球從O點運動到最低點的過程中只有重力做功,所以

圖2
小球的受力情況如圖2所示.由牛頓第二定律
由以上兩式得
(3)小球受電場力和重力的合力向上,將向上運動,同時受洛倫茲力,運動類型和只受重力和洛倫茲力時相同,所以在最高點時速度最大,根據(jù)題意,可大膽地猜想得出,在最高點時曲率半徑仍為該點到x軸距離的2倍.所以
再由動能定理得
可得
解法2:從運動的合成與分解的角度進行分析
帶電粒子受到恒定的力F(忽略重力)在勻強磁場B中,從坐標原點O無初速度的開始運動,可從運動分解的角度把初速度分解為一個沿x軸正方向的速度v和一個沿x軸負方向的速度v′=v,且qvB=F,這樣小球的運動可看作是初速度為v′的勻速圓周運動,向心力為qv′B,和圓心沿x軸正方向的速度為v的勻速直線運動的合運動.釋放點O為小球運動的最高處,即圓周運動的最高處,如圖1所示,當小球運動到最低點時,小球運動的速度為2v,小球運動的合外力為
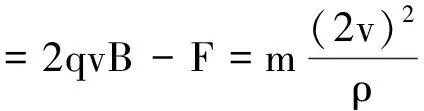
式中的ρ為運動軌跡最低處的曲率半徑.而在圓心參考系中,有
式中R為圓周運動的圓半徑,由以上兩式可得ρ=4R,即得到在平行于y軸方向向下恒力F的作用下,小球從靜止開始在勻強磁場中做曲線運動時,當它運動到最低處運動軌跡的曲率半徑等于該點到x軸的2倍.可見,這種結(jié)論具有普適性.
解法3:用動量定理分析[主要分析第(2)問]
題上已知條件是小球運動軌跡曲線在最低點時的曲率半徑為該點到x軸距離的2倍,事實上這個條件是可以證明出來的,是普適的.
證明如下:
小球在重力和洛倫茲力的作用下做曲線運動,重力為恒力,洛倫茲力總與速度垂直,小球做曲線運動.
運動中任意位置的受力情況如圖2所示.在圖3中,v為這一時刻的瞬時速度,vx,vy為這一時刻的水平和豎直分速度.
qvyB,qvxB為這一時刻洛倫茲力的水平分量與豎直分量.
從這一時刻起,經(jīng)極短一段時間Δt,列水平方向的動量定理式子
qvyBΔt=mΔv
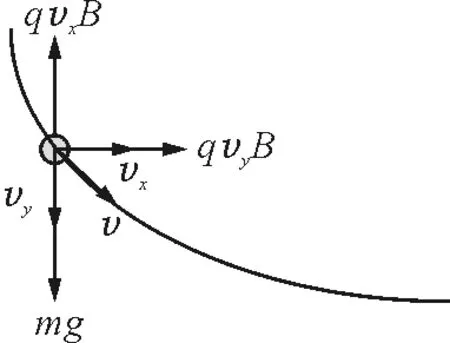
圖3
式中Δv為時間Δt內(nèi)水平方向的速度增量.對于小球,把它從O點到最低點的過程中,時間分成無數(shù)個Δt,對于每一個Δt都可以列出一個水平方向的動量定理方程,再把這些方程求和,即
可得
qBym=mv1
(1)
由動能定理
(2)
由式(1)、(2)可得
再由最低點牛頓第二定律得
(3)
聯(lián)立式(1)、(2)、(3)可得R=2ym
可見,當小球運動到最低點時,曲率半徑一定等于該點到x軸距離的2倍.
第(3)問和第(2)問方法相同,仍利用水平方向動量定理.
這道題是一個復(fù)雜的復(fù)合場的題目,筆者從3個方面用3種方法分析了這道題,當然大家可能還有其他的解法,通過分析可以對這種題型有一個更加清晰的理解.教師在教學(xué)中也應(yīng)當對重要的題型多加鉆研,鼓勵學(xué)生學(xué)會發(fā)散思維.經(jīng)常一題多解,可以鍛煉思維能力,擴大視野,提高解題的靈活性.
參考文獻
1 李泓斌.對兩道高考題的分析及引發(fā)的思考.中學(xué)物理,2009,29(13):40

