多單元永磁同步電機數學模型與轉矩波動抑制

鄒繼斌，趙博，梁維燕，2，徐永向

(1.哈爾濱工業大學 電氣工程系，黑龍江 哈爾濱150001;2.哈爾濱電站設備集團公司，黑龍江 哈爾濱150040)

0 引言

大功率低速大扭矩永磁同步電機在國防與國民經濟中有越來越廣泛的需求，如船舶及戰艦推進、軋鋼、石油礦山等[1]。然而，隨著這種直驅式永磁同步電機的功率逐漸升高，其系統對功率器件的等級要求隨之升高，這也限制了大扭矩永磁直驅電機的發展。為解決電機容量與功率器件等級的矛盾關系，大功率永磁電機的設計多采用多單元或者多相化設計，不但可以降低驅動支路的容量，而且還具備一定的容錯運行能力。

多單元電機是指電機本體包含多個單元電機，每個單元獨立連接一臺三相驅動器，各單元電機及驅動器可以同時運行，也可以部分單元運行。永磁多相電機與多單元電機的區別不僅體現在本體設計上，還體現在驅動器拓撲結構和控制策略上[2－3]。多相電機在運行時，控制上較復雜[4－5]。相比較而言，多單元電機控制簡單，若某一支路繞組出現開路故障時，可將故障單元電機切除，其余單元電機相電流維持不變，不必調整其幅值相位，容錯運行非常方便[6]。各個單元電機雖在電路上并不相連，但是因各單元電機繞組共用一個定子鐵心，存在磁路上的耦合關系。當轉子磁極為凸極結構時，因繞組空間間距并不相同，將引起繞組間互感不平衡，而在三相對稱電流條件下，互感中二次項的不對稱將引起定子側磁阻轉矩波動。針對該類轉矩波動給出注入3次諧波電流的進行抑制方法[7]。最后，采用數值分析和試驗驗證的方法對所得的解析公式進行相關印證。

1 多單元電機的電壓方程

以一臺額定功率2 MW額定轉速100 r/min的5單元永磁同步電動機為研究對象，其系統拓撲圖如圖1所示。

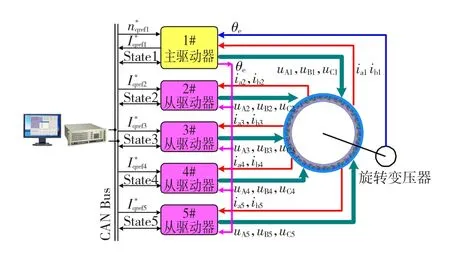
圖1 2 MW五單元永磁同步電動機系統Fig.1 2 MW five units PMSM system

因多單元電機單元內部及單元電機間繞組互感不完全相同，所以傳統三相電機或多相電機的數學模型無法直接應用于多單元電機分析中，因此有必要建立其相關數學模型。

1.1 多單元電機整機運行時的電壓方程

以五單元電機為例，為簡化電壓表達式，采用分塊矩陣的方式進行整機電壓方程列寫，其方程為

式中:Ui和Ii(i=1，2，3，4，5)表示每個單元的三相電壓和電流列矩陣;Ra為每相繞組電阻;If為轉子永磁體等效勵磁電流;L為每個單元電機內部的三相繞組電感矩陣;Mij(i，j=1，2，3，4，5，i≠j)為各個單元間的互感矩陣;MTij(i，j=1，2，3，4，5，i≠j)為單元間互感矩陣的轉置;Msri(i=1，2，3，4，5)是每個單元電機定、轉子之間互感矩陣，其表達式完全相同。

每個單元電機的三相電流完全對稱，所有單元共同運行時，可等效為三相電機。

1.2 單元電機內部的三相電感矩陣

因為每個獨立的單元電機三相繞組僅僅占據定子空間一部分扇區，所以三相繞組在空間上互感磁鏈不完全相等，這將引起同一單元電機內部三相繞組間互感不完全一致。對多單元電機進行有限元數值分析，可以得到空載時一個單元電機內的三相繞組互感系數，如圖2所示。

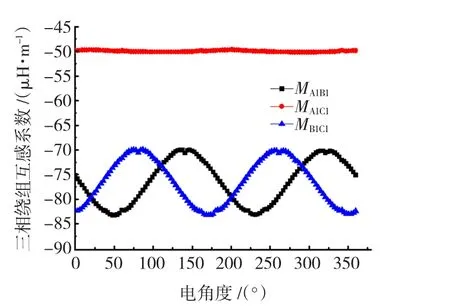
圖2 單元電機內部繞組互感系數Fig.2 Coefficient of mutual inductances in one unit motor

計算結果反應出，單元電機內部存在嚴重的互感不對稱現象，由于轉子采用了凸極結構，所以電感中含有2次波動項。不同單元電機內部電感矩陣完全一致，在此僅給出1號單元電機的電感矩陣及各元素表達式，即

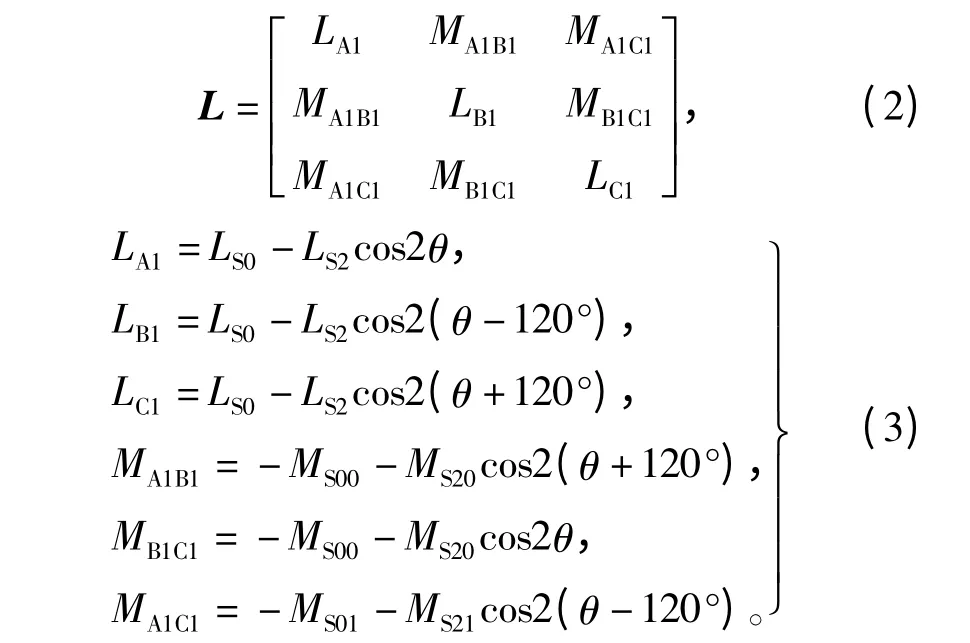
式中:互感恒定分量與二次波動分量滿足不等式MS00＞MS01，MS20＞MS21;互感下角標第一個數字0代表其恒定分量，2代表其二次分量;互感下角標第二個數字表示兩相繞組中間間隔繞組的相數，0表示兩繞組緊鄰，1表示兩繞組中間間隔一相繞組，其余與之類似。

1.3 不同單元電機間的互感矩陣

多單元電機這種非對稱共磁路的繞組拓撲結構不僅僅引起單元電機內部三相繞組互感不對稱，還會引起單元電機間各相繞組互感也不相等。因單元電機圓周循環排布，公式(1)中的各個單元電機間互感矩陣的函數關系式為

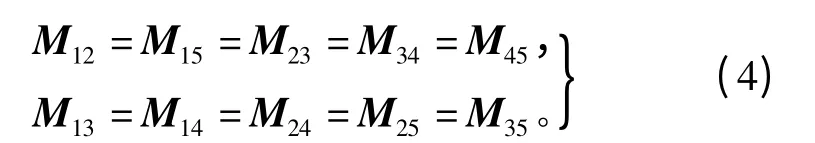
在此，僅列寫1號與2號單元電機間的互感矩陣，其余各單元電機間互感矩陣可對應依照給出。1號與2號單元電機間互感矩陣為

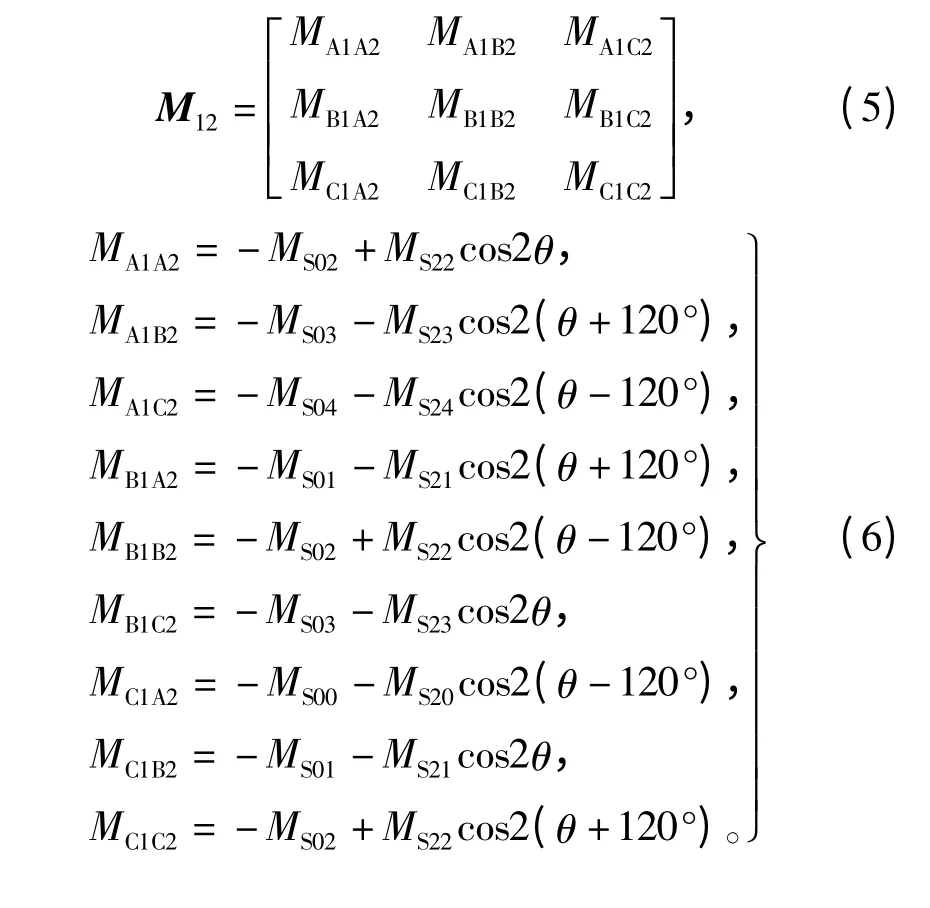
其中，有如不等式(7)所示的關系成立，即

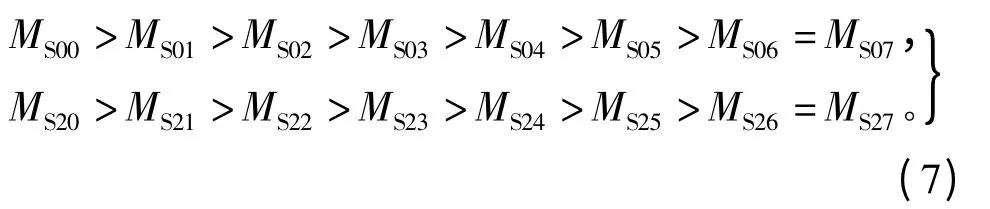
1.4 部分單元電機運行時的電壓方程

多單元電機某一相繞組發生開路故障時，可以直接將故障單元整體切除，而剩余的工作繞組仍可繼續維持電機的正常運行，且各單元繞組中的電流幅值和相位無需再次進行調整。

在此，假設僅1號、2號和3號相鄰三單元共同運行，則部分單元運行時的電壓方程可以列寫為

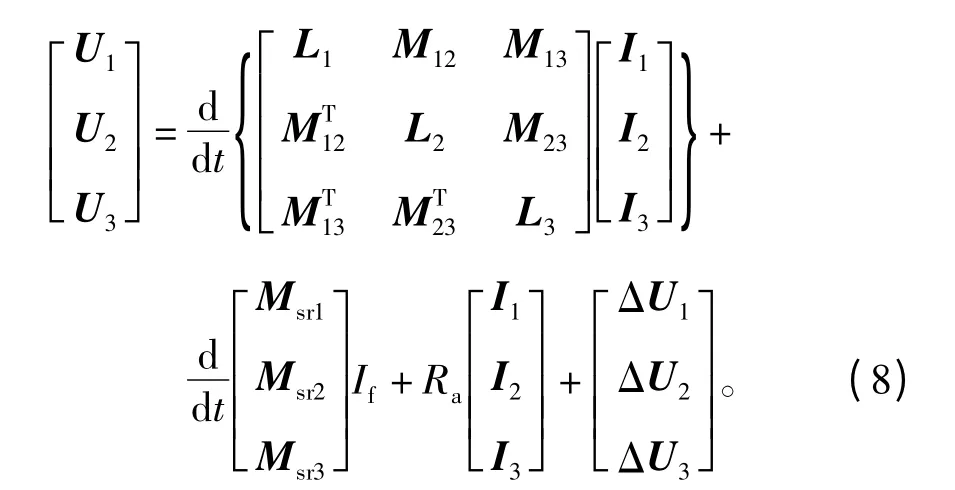
其中，ΔU1、ΔU2和ΔU3是單元電機Y接繞組中點與三相Y接電源中點間的電位差列矩陣。部分單元電機運行時，單元間互感不平衡，每相繞組的阻抗并不完全一致，因此繞組中點與電源中點將存在一個電位差，這一現象在傳統三相對稱電機系統中并不存在。

由于各單元三相支路電抗不相等，所以部分單元運行時，若采用的是對稱三相電壓源，則必然會產生三相不對稱電流，其定子電流中將含有一定成分的負序分量。同樣，假定部分單元電機運行時，各單元三相繞組外接對稱三相電流源，則每單元的三相繞組端電壓將不再對稱。

2 多單元電機的電磁轉矩方程

2.1 三相對稱電流時的恒定電磁轉矩

在此，假定各個單元電機的激勵源為幅值相等的三相嚴格對稱的電流源，采用磁共能法計算多單元電機整機運行時的電磁轉矩，其轉矩矩陣表達式可以寫為

式中p為電機的極對數。上述矩陣表達式可以進一步簡化為

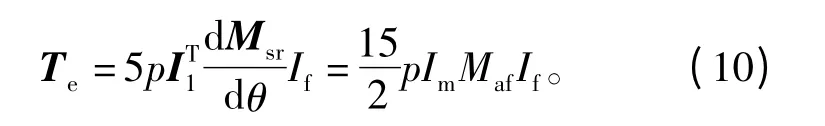
式中:Im是相電流的幅值;Maf是定轉子互感的幅值。

僅部分單元電機工作時，仍可用式(9)對轉矩進行計算，僅需要將不工作單元的電流矩陣給為0即可。例如，僅1號和3號單元電機運行，則電磁轉矩方程可以化簡為

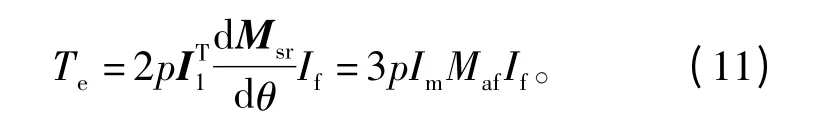
對比整機運行與部分單元運行時的恒定轉矩表達式可以看出，兩單元電機運行時，在相同電流下，其輸出電磁轉矩是整機運行時的40%。且在同一相電流下，電機對外輸出的電磁轉矩與運行單元空間位置無關，僅與運行單元數量相關。

2.2 三相對稱電流下部分單元運行時的轉矩波動

在三相對稱電流下，因為單元電機內部及單元電機間的互感不完全對稱，所以部分單元運行時，將會引起磁阻轉矩波動。該轉矩波動主要是由定子繞組互感不對稱引起，且該轉矩波動數值以及規律不僅與部分單元的運行個數相關，還與運行單元所處的空間排布位置有關。

假設運行的單元電機采用正弦三相對稱電流源驅動。當僅1號單元電機獨立運行時，其轉矩波動可以寫為

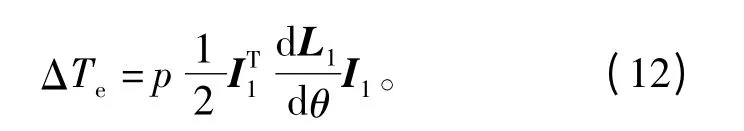
將電感與電流表達式帶入公式(12)中，化簡后可得一個單元電機運行時的轉矩表達式為

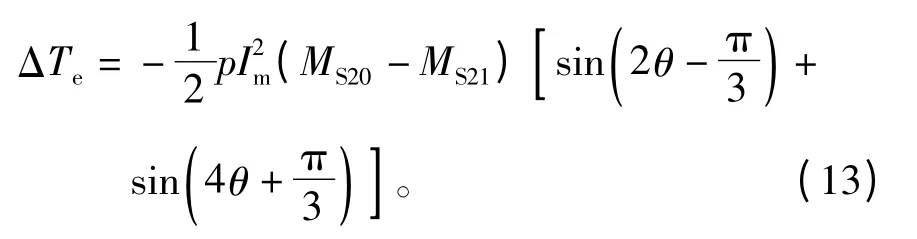
從上述表達式中可以看出，一個電周期轉矩波動為2次和4次，其幅值與定子繞組電流幅值平方和互感二次波動項的差值成正比。由此也可以看出，在三相對稱電流條件下，若多單元電機為嚴格的隱機電機時，互感不對稱并不引起轉矩波動，但仍會引起單元電機三相端電壓不對稱。

與1個單元電機運行類似，空間不同位置的單元電機組合運行時，也含有2次和4次轉矩波動，但是其幅值將有所不同。

1#、2#兩相鄰單元電機運行時轉矩波動為

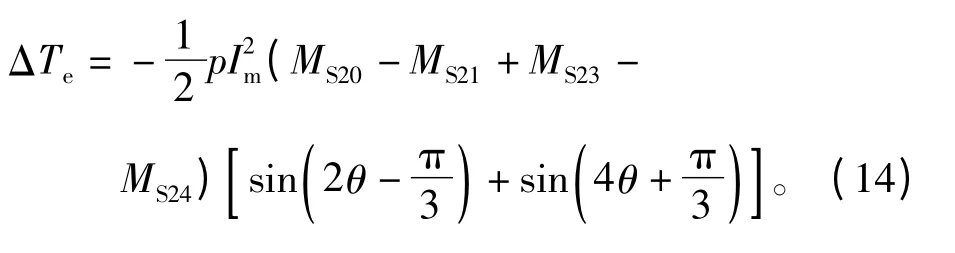
1#、3#兩單元電機間隔一個單元運行時的轉矩波動為

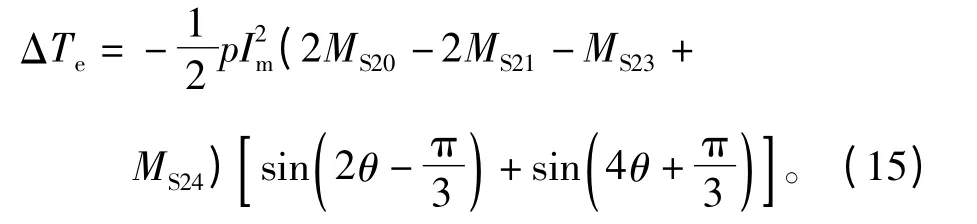
1#、2#和3#三個單元電機相鄰運行時的轉矩波動為

1#、2#以及4#兩相鄰單元與1個間隔單元電機匹配運行時的轉矩波動為

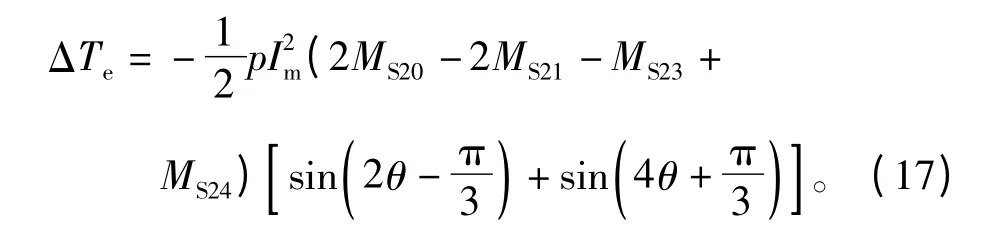
1#～4#四個單元電機運行時的轉矩波動表達式與僅1#單元運行時的表達式完全相同，在此不再重復列寫。而當所有單元運行時，轉矩波動將為零。

繞組間互感二次項隨兩繞組空間距離的增加而迅速降低，因此轉矩波動主要是由相鄰兩繞組、間隔一相的兩繞組的互感二次項之差決定。此外，通過公式可以看出，幾個相鄰單元電機運行時，其轉矩波動與一個單元電機運行時相同，而采用間隔單元運行時，則轉矩波動將會增加一倍。在此，采用有限元法，對僅1號和2號單元電機運行的轉矩波動進行計算，得到了電流與轉矩波動之間的關系，如圖3所示。

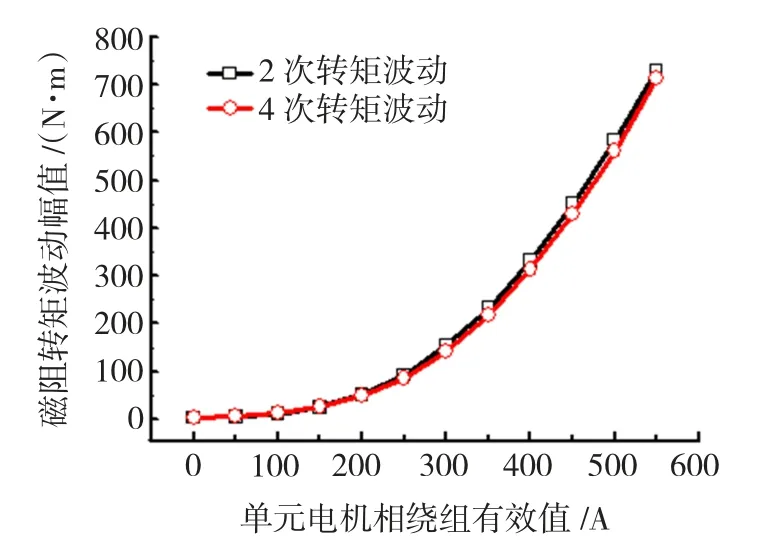
圖3 僅1、2號單元運行時電流與轉矩波動曲線Fig.3 Current and torque ripple amplitude relation when No.1 ＆2 unit motors running

從轉矩波動計算結果可以看出，2次與4次轉矩波動幅值一致，且與相電流成二次函數關系，這與轉矩波動解析推導公式相吻合。

3 部分單元運行時轉矩波動的抑制

部分單元電機運行時，因為單元內部與單元間繞組互感不對稱，而普通三相電機并不含有該類轉矩波動。通過計算可知互感不對稱引起的波動量為1.26%，試驗值為1.55%，因由飽和效應引起的轉矩波動尚未計算在內，所以試驗數據比計算數據稍大。部分單元電機運行時的2次和4次轉矩波動頻率較低，對系統的影響尤為明顯，所以需要采用一定的抑制轉矩波動的措施。

最為直接的是采用諧波電流注入法進行轉矩波動抑制，注意到轉矩波動為幅值相等的2次和4次波。可分別注入3次和5次正序諧波電流，或1次和3次負序諧波電流，在滿足一定幅值、相位條件時諧波電流與基波磁場相作用，即可抵消轉矩波動。其中，正序3次電流可抵消2次波動，負序3次電流可抵消4次波動。為得到更為簡潔的注入諧波方式，可同時注入正、負序的3次諧波電流。

假定三相繞組激勵源為三相對稱正弦電流，僅一個單元電機運行，諧波電流引起的轉矩波動可表為

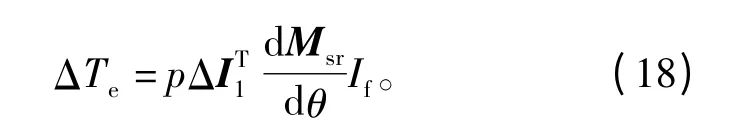
經過推導后可知，在滿足相位約束條件時的三相正序和負序3次諧波電流合成后的三相電流表達式為

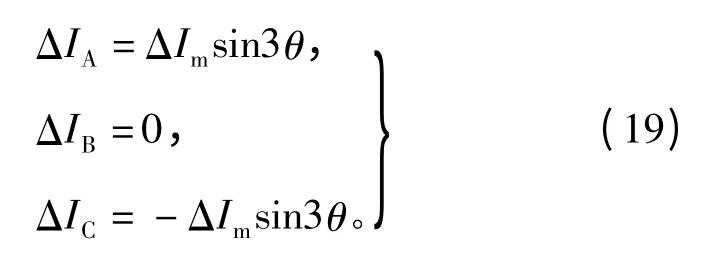
因2次和4次轉矩波動的幅值相等，所以正、負序電流幅值也相等，其表達式為

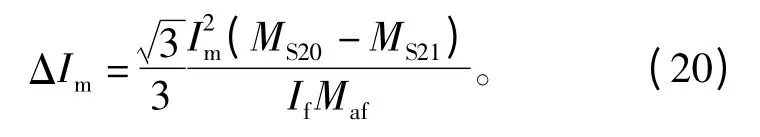
本文計算了一個單元電機運行時，在繞組500 A條件下，注入18 A諧波電流前后的轉矩波動曲線，如圖4所示。

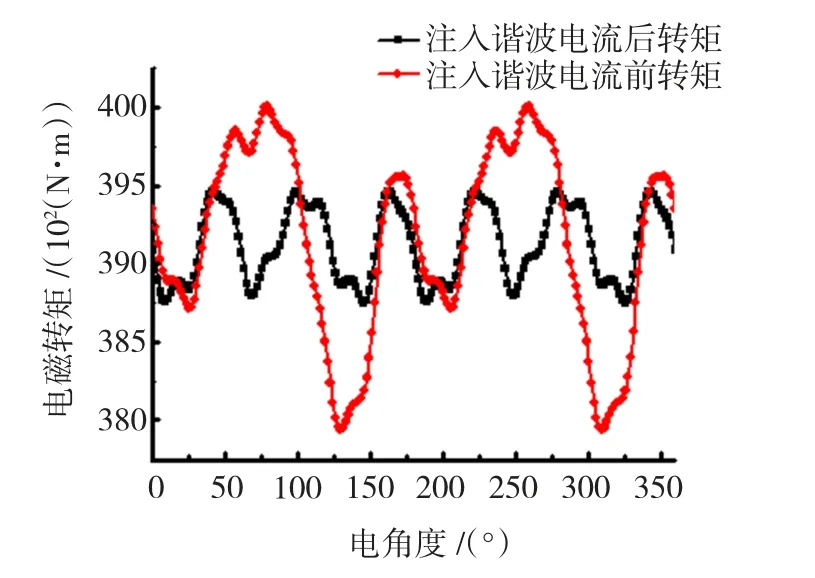
圖4 注入諧波電流前后的轉矩波動曲線Fig.4 Inject currents before and after torque ripple curve

通過圖4的轉矩曲線對比可以看出，轉矩波動得到了最大程度的抑制，轉矩波動降低了3.5%。此時電機轉矩波動中僅含有飽和引起的6次轉矩波動成分。當部分單元電機運行時，可以僅選擇一個固定單元注入諧波，其余單元仍施加三相對稱基波電流。

4 多單元電機相關試驗

4.1 單元電機電磁轉矩與單元個數關系試驗

針對不同單元數量運行，進行相關試驗，并與有限元計算結果進行橫向對比。計算與試驗結果曲線如圖5所示。

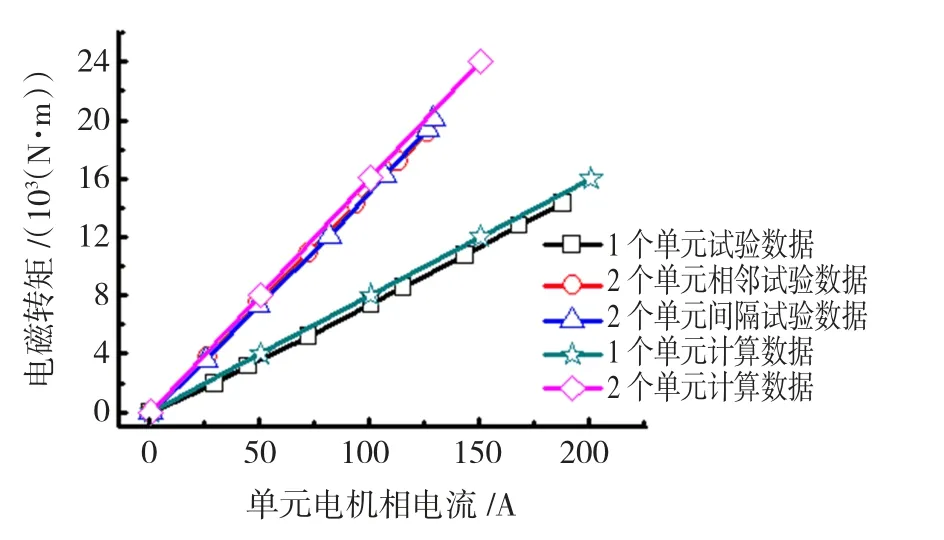
圖5 不同單元運行時的試驗與計算數據對比Fig.5 Test and calculation data of different units running

通過圖5可以看出，計算數據與試驗數據吻合度較高，且隨著單元個數增加，同一電流時，整機轉矩將成正比增加，轉矩數學模型與試驗結果相吻合。

4.2 部分單元運行時的轉速波動

轉矩波動公式的推導是基于三相對稱電流源基礎之上。因為多單元電機驅動器采用是三相對稱電壓源，繞組電流將含有三相負序分量，該負序電流將產生2次轉矩波動。因樣機直接測試轉矩波動困難，所以通過測定轉速波動來反映轉矩波動規律。2 MW樣機的轉速波動曲線如圖6所示。

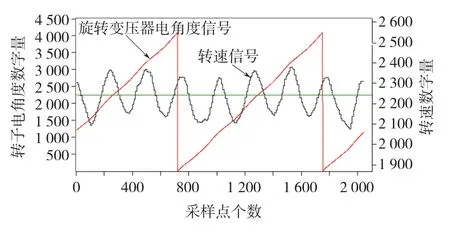
圖6 一個單元電機運行時的速度波動曲線Fig.6 Speed ripple of one unit motor running

從圖6中可以看出，在一個電周期內，電機的轉速波動為4次，該次波動在普通三相電機中是不存在的，而這正是多單元電機的特點之一。

5 結語

本文針對多單元永磁同步電機繞組互感不對稱的特殊性，建立了其在自然坐標系下的整機及部分單元運行時的電壓方程和轉矩方程。分析了在部分單元電機運行時電磁轉矩波動的解析表達式，并在此基礎之上，給出了采用注入正序、負序3次諧波電流抑制轉矩波動的方法，并得到了所需注入諧波電流的解析表達式。數值分析及相關試驗表明，本文所推導的多單元永磁同步電機數學模型正確，轉矩波動的抑制方法有效。除此之外，上述結論還可用以對不同單元數量的多單元永磁同步電機進行分析。

[1]LEILA P，HAMID A.Five-phase permanent magnet motor drives for ship propulsion applications[J].IEEE Electric Ship Technologies Symposium，2005，12(7):371－378.

[2]向東，于飛.考慮阻尼繞組的五相PMSM數學模型及等效電路[J].電機與控制學報，2008，12(6):644－649.XIANG Dong，YU Fei.Mathematical models and equivalent circuits of five-phase PMSM including damper windings[J].Electric Machines and Control，2008，12(6):644 －649.

[3]MARTIN J，SLOBODAN N Vukosavic，EMIL Levi.Parallel-connected multiphase multi-drive systems with single inverter supply[J].IEEE Transactions on Industrial Electronics，2009，56(6):2047－2057.

[4]歐陽紅林，周馬山，童調生.多相永磁同步電動機不對稱運行的矢量控制[J].中國電機工程學報，2004，24(7):145－150.OUYANG Honglin，ZHOU Mashan，TONG Tiaosheng.Vector control of multi phase permanent magnet synchronous motor with asymmetric structure[J].Proceedings of the CSEE，2004，24(7):145－150.

[5]ZHU Jingwei，NESIMI Ertugrul，SONG Wenliang.Minimum torque ripple current control strategy in a dual fault tolerant PMAC motor drive[C]//2008 IEEE Power Electronics Specialists Conference，June 15 － 19，2008，Rhodes，Greece.2008:1542－1547.

[6]ZHANG Bingyi，LIU Yu，FENG Guihong.Study on low voltage high-power multi-branch permanent magnet synchronous motor[C]//Power and Energy Engineering Conference，March 28－31，2010，Chengdu，China.2010:1－4.

[7]張經緯，祝后權，黃振華，等.多相集中整距繞組感應電機的建模與仿真[J].電機與控制學報，2010，14(9):75－80.ZHANG Jingwei，ZHU Houquan，HUANG Zhenhua，et al.Modeling and simulation of a multiphase concentrated induction Machine[J].Electric Machines and Control，2010，14(9):75 －80.