75 kg/m鋼軌12號高錳鋼固定轍叉單開道岔剛度均勻化設計研究

陳 嶸,王 平

(西南交通大學高速鐵路線路工程教育部重點實驗室,成都 610031)

軌道剛度是影響列車運行平穩性和軌道結構工作性能的重要參數之一[1],國內外學者曾對區間線路軌道剛度的取值及部件剛度合理匹配進行了大量研究[2-4]。近年來,伴隨我國高速鐵路技術的快速發展,高速道岔區軌道剛度合理設置研究也取得突出進展[5-7]。大軸重、高密度和大運量是我國重載鐵路的三大特征(2010年大秦鐵路年運量已突破4億t),在這種極其嚴峻的運輸條件下,岔區不均勻剛度勢必加劇輪軌系統動力響應,影響列車運行平穩性,增大軌道部件動應力,道岔部件的傷損遠大于普通線路道岔,存在嚴重的鋼軌垂磨、側磨、壓潰、掉塊等特有問題[8]。然而,重載道岔與高速道岔在服役性能上存在較大差異,需要專門研究固定轍叉重載道岔軌道剛度的分布規律,并采取均勻化措施,使道岔軌道剛度沿線路縱向分布均勻,以滿足重載列車運行平穩和延長道岔使用壽命的需要。

為此,針對75 kg/m鋼軌12號高錳鋼固定轍叉單開道岔，應用有限單元法,考慮剛度的各種影響因素,建立起整組道岔軌道剛度計算模型，分析岔區軌道剛度分布規律,在此基礎上討論了岔區軌道剛度均勻化措施及板下膠墊剛度設計。

1 固定轍叉道岔軌道剛度計算模型

重載道岔一般采用有砟軌道,鋼軌支點剛度等同于扣件剛度與道床路基剛度的串聯組合剛度。其中,道床和路基的剛度隨著路基和道床結構確定下來也隨之確定,一般不易進行大幅度調整,而扣壓件和軌下膠墊的剛度可以較為方便地進行調整,因此扣件和膠墊剛度的大小直接影響到軌道整體剛度的大小。

在充分考慮扣壓件、鐵墊板及板下膠墊、鋼軌類型、滑床臺等影響因素的基礎上,采用有限元法建立了75 kg/m鋼軌12號固定轍叉單開道岔的軌道剛度計算模型。模型中將基本軌、護軌用等截面梁來模擬；尖軌、心軌用變截面長梁模擬；扣壓件和軌下膠墊簡化成線性彈簧；鐵墊板為等截面彈性地基短梁；板下膠墊剛度采用彈性地基系數模擬；尖軌和滑床臺的聯結采用單向傳力彈簧來模擬,該彈簧只在受壓時傳力,受拉時不傳力。每種單元類型具有不同的形函數和單元剛度矩陣[9]。道岔整體模型沿縱向劃分為尖軌尖端前、轉轍器部分、導曲線部分、導曲線共用墊板部分和轍叉部分5類,其中轉轍器和轍叉部分模型如圖1、圖2所示。

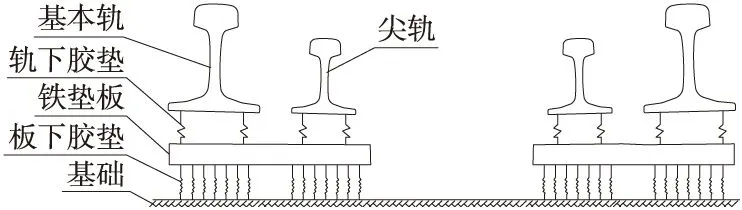
圖1 轉轍器部分模型

圖2 轍叉部分模型

2 計算參數

75 kg/m鋼軌12號固定轍叉單開道岔的基本軌采用我國75 kg/m鋼軌制造,尖軌采用60AT軌制造,護軌采用UIC33槽型鋼制造,各種鋼軌截面參數如表1所示。

表1 各種鋼軌截面參數

鋼軌彈性模量為206 GPa,泊松比0.3。Ⅱ型彈條扣壓力取為10 kN,彈程為10 mm,則其剛度取為1 kN/mm。Ⅲ型彈條扣壓力取為11 kN,彈程為13 mm,則其剛度為0.85 kN/mm。

3 岔區軌道剛度分布規律

若共用板下膠墊的材質與溝槽開設方式與普通板下膠墊相同,則其剛度與普通板下膠墊的剛度成比例關系。以70 kN/mm普通板下膠墊作為剛度基準,計算各塊共用板下膠墊的剛度值,分析未采取均勻措施時的岔區軌道剛度分布規律。軌道剛度計算結果如圖3、圖4和表2所示,表2中所列為計算結果最大值。

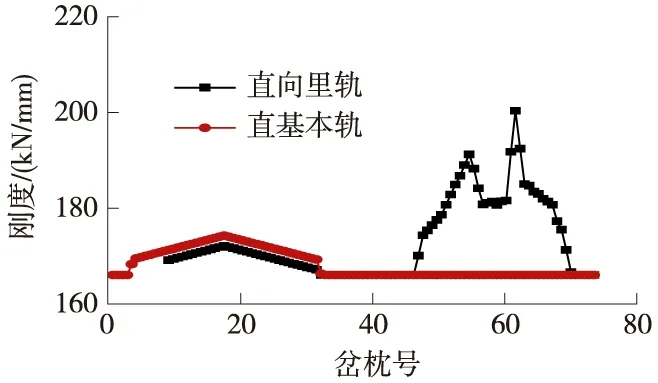
圖3 直向過岔整體剛度

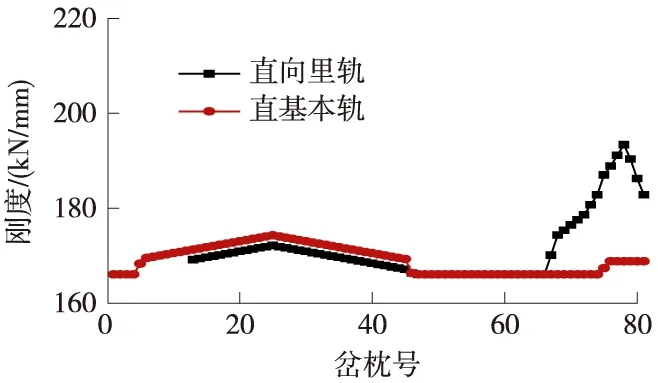
圖4 側向過岔整體剛度

表2 軌道剛度計算結果最大值

從圖3和圖4可看出以下規律。

(1)直基本軌的軌道整體剛度在轉轍器部分約為175.68 kN/mm,在其他區段約為170 kN/mm,轉轍器部分軌道整體剛度較其他區段大6 kN/mm左右。這是由于在轉轍器部分,基本軌和尖軌共用鐵墊板,且板下膠墊的剛度較大所致。

(2)曲基本軌的整體剛度大小、分布規律與直基本軌在轉轍器及導曲線部分大致相同,但在心軌尖端附近,由于和護軌共用較大剛度的板下膠墊,并且護軌幫軌作用的影響,曲基本軌的整體剛度在護軌區段突然增大至178 kN/mm,增幅在2 kN/mm左右。

(3)直向和側向里軌的剛度變化規律基本相同：轍叉部分剛度最大,轉轍器部分次之,連接部分最小,其中轉轍器部分剛度增大是由于共用板下膠墊剛度較大和基本軌的幫軌作用,轍叉部分剛度增大是由于錳叉下大剛度板下膠墊和鋼軌抗彎剛度增加所致。轍叉部分剛度變化主要是由錳叉心軌抗彎剛度縱向變化引起的,總體上存在2個峰值。

(4)直、側向過岔在軌道的橫向和縱向均存在較大的剛度不平順,其中以錳叉區段不平順幅度最大。

4 道岔剛度均勻化

對重載12號固定轍叉道岔,由于扣件系統的剛度較大,可按膠墊分布支承鐵墊板方式均勻軌道剛度,如圖5所示。根據軌道剛度及其變化率合理及工程上便于實現等均勻化原則,經輪軌系統動力學分析,固定轍叉重載道岔合理的扣件剛度值如下：軌下膠墊剛度為350 kN/mm；在20～60 kN荷載作用下,板下膠墊剛度為(70±10) kN/mm設計；在60～100 kN荷載作用下,板下膠墊剛度為(300±10) kN/mm,板下膠墊剛度特性呈雙線性。

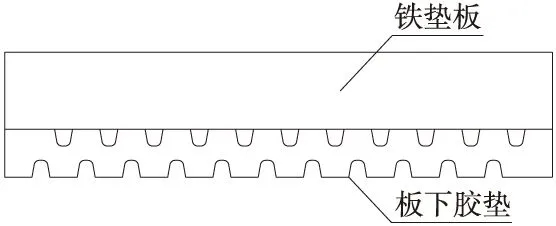
圖5 膠墊分布支承鐵墊板

對重載12號固定轍叉單開道岔板下膠墊雙線性剛度設計方法如下：運用道岔軌道剛度計算方法,對每塊膠墊先按第一段線性剛度進行計算,然后根據膠墊分段線性剛度之間的關系定義出其余分段的線性剛度。均勻化時,所有軌下膠墊的剛度保持在350 kN/mm不變,普通鐵墊板(長度為432 mm,支承1根鋼軌)下的分布支承式膠墊剛度設為70 kN/mm。對于共用墊板下的膠墊剛度,先對多種優化方案進行計算,然后根據均勻化原則通過比選確定一種最優方案。

表3為剛度優化后每一塊板下膠墊的剛度值,表中括號內的剛度值為雙線性膠墊剛度的第二段線性剛度。為鋪設和更換方便,鐵墊板下共用橡膠墊板的編號與道岔平面總布置圖中的岔枕編號相同。在轉轍器部分,直股和側股鋼軌在同一岔枕上使用相同編號的板下膠墊。

表3 分布支承板下膠墊剛度優化結果

圖6和圖7分別為12號固定轍叉單開道岔采取均勻化措施后,直向軌道整體剛度和側向鋼軌撓度沿線路縱向變化率與均勻前的對比。

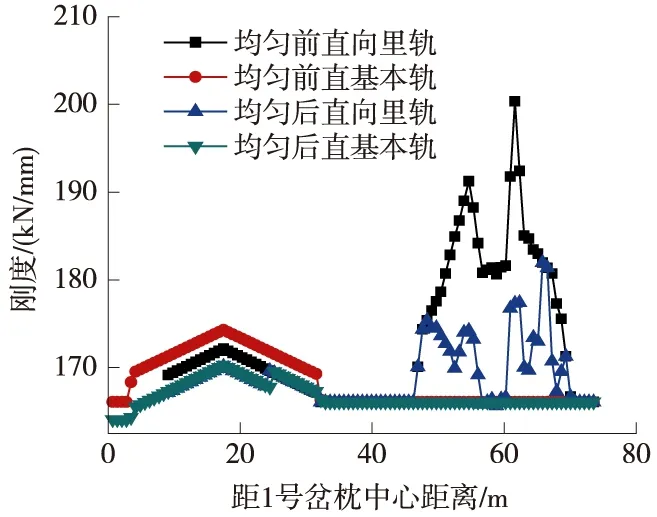
圖6 直向過岔均勻前后整體剛度

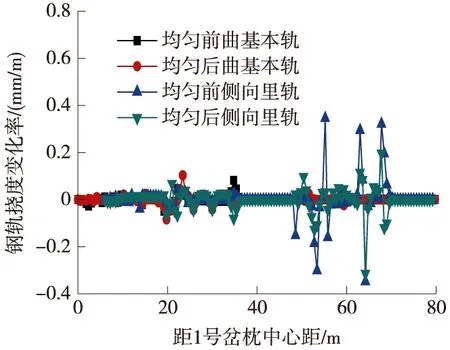
圖7 側向過岔鋼軌撓度變化率

由表3和圖6、圖7可知：

采取均勻化措施后,直、曲基本軌的整體剛度沿線路縱向基本呈水平分布,只在轉轍器前部有微小波動。直、側向里軌的整體剛度分布規律相同,均保持在175 kN/mm左右，沿線路縱向水平分布,僅在轍叉中心區域有較小波動,最大波動幅度僅8 kN/mm。有效降低了鋼軌撓度變化率,并使所有鋼軌撓度變化率小于0.3 mm/m,如直向里軌的最大撓度變化率從均勻前的0.36 mm/m降至均勻后的0.13 mm/m。

5 板下膠墊剛度設計

在列車荷載作用下,橡膠墊板剛度隨枕上壓力的變化表現出非線性特性,既可提供彈性又可控制軌道變形,而固定轍叉重載道岔的板下膠墊剛度要求相對較大,因此可采用膠墊支承面開設溝槽的方式進行剛度調整。板下膠墊開設溝槽后,存在的主要問題是,在溝槽底部邊緣容易引起應力集中,并且橡膠的受力變形由開設前的簡單壓縮變成開設后的壓縮、彎曲和剪切組合,使得膠墊應力增加,使用壽命降低。

在影響膠墊強度的眾多因素中,除膠墊材料的力學特性外,溝槽的寬度、深度、相鄰溝槽的中心距以及溝槽形式都是影響膠墊強度的主要因素。因此,需要對板下膠墊的溝槽進行合理的設計,使其剛度滿足設計要求的同時,板下膠墊具有足夠的強度和耐久性。

本文運用超彈性有限元方法[10]對固定轍叉重載道岔的板下膠墊剛度進行設計。通過多方案比選計算,最終確定表4所示的溝槽開設方式為板下膠墊剛度優化設計結果。圖8為普通板下膠墊在100 kN枕上壓力作用下的等效應力分布。板下膠墊的等效應力最大值對應軌底中心,板下膠墊即使在100 kN枕上壓力作用下,其最大等效應力為2.867 MPa,小于容許限度3 MPa,按表4所示方式開設溝槽的板下膠墊強度能滿足使用要求。

圖8 普通膠墊在100 kN枕上壓力作用下的等效應力分布

需要說明的是,按表4所列方式開設溝槽的板下膠墊,其計算剛度與表3所列剛度的誤差在5%～15%以內,表明按表3所列方式對板下膠墊開設溝槽,基本能實現固定轍叉重載道岔的軌道剛度均勻化。

6 結論與建議

(1)75 kg/m鋼軌12號固定轍叉重載單開道岔如不采取剛度均勻化措施,直、側向軌道剛度將存在較大的不均勻性,其中以錳叉區段的剛度不均勻幅度最大。

(2)采用350 kN/mm的軌下膠墊剛度,并采用表3所列的板下膠墊剛度,基本能使75 kg/m鋼軌12號固定轍叉重載單開道岔的軌道剛度沿線路縱向均勻變化,從而提高列車過岔的安全性和平穩性,改善道岔部件的力學性能,延長設備使用壽命和減少養護維修工作量。

(3)采用表4所列方式對75 kg/m鋼軌12號固定轍叉重載單開道岔的板下膠墊開設溝槽實現剛度調整,膠墊強度能夠滿足使用要求。

[1] LOPEZ P A. The vertical stiffness of the track and the deterioration of high speed lines[J]. Revista de Obras Publicas, 2001(11):7-22.

[2] Wu T X, Thompson D J. The effects of local preload on the foundation stiffness and vertical vibration of railway track[J]. Journal of Sound and Vibration, 1999,219(5):881-904.

[3] 趙國堂.鐵路軌道剛度的確定方法[J].中國鐵道科學,2005,26(1):1-6．

Zhao Guotang. Method for Determining the Rigidity of Railway Track[J]. China Railway Science, 2005,26(1):1-6．

[4] 羅雁云,朱劍月.線路道岔軌下剛度改變對輪軌動力性能影響研究[J].電力機車與城軌車輛,2004,27(5):9-12．

Luo Yanyun, Zhu Jianyue. Investigation on dynamic characteristic of wheel/rail by changing the stiffness under the railway track turnout[J]. Electric Locomotives & Mass Transit Vehicles, 2004,27(5):9-12.

[5] 陳小平,王平.無砟道岔軌道剛度分布規律及均勻化[J].西南交通大學學報,2006,41(4):447-451.

Chen Xiaoping, Wang Ping. Distribution Regularity and Homogenization of Track Rigidity for Ballastless Turnout[J]. Journal of Southwest Jiaotong University, 2006,41(4):447-451.

[6] 陳小平,王平.時速350 km客運專線無砟道岔的合理軌道剛度研究[J].鐵道標準設計,2010(3):1-3.

Chen Xiaoping, Wang Ping. Research on Reasonable stiffness of Non-ballasted Turnout in 350 km/h PDL[J]. Railway Standard Design, 2010(3):1-3.

[7] 王平,陳嶸,陳小平.高速鐵路道岔設計關鍵技術[J].西南交通大學學報,2010,45(1):28-33.

Wang Ping, Chen Rong, Chen Xiaoping. Key Technologies in High-Speed Railway Turnout Design[J]. Journal of Southwest Jiaotong University, 2010,45(1):28-33.

[8] 左玉良.重載快速區段固定型提速道岔轉轍部位直股鋼軌側磨的研究[J].鐵道標準設計,2005(1):53-56.

Zuo Yuliang. A Research on Side Abrasion of Straight Rail of Fixed Type Speed Increase Turnouts at Heavy Haul Rapid Section[J]. Railway Standard Design, 2005(1):53-56.

[9] 王勖成.有限單元法[M].北京：清華大學出版社,2003.

Wang Xucheng. Finit element Method[M]. Beijing: Tsinghua University Press, 2003.

[10] 徐明.橡膠類超彈性材料本構關系研究及有限元分析(博士學位論文)[D].北京：北京航空航天大學,2002.

Xu Ming. A Study on Nonlinear Constitutive Law and FEA of Rubber-Like Hyperlastic Materials[D]. BeiJing University of Aeronautics & Astronautics, PHD Thesis, 2002.