Logistic模型的幾何凸性、彈性及其應用

汪維剛

(桐城師范高等專科學校理工系，安徽桐城231402)

1．Logistic模型的幾何凸性、彈性

1．1 模型簡介

它是Malthus模型的拓展。該模型:N=N0en，與實際情況不夠吻合，為此，修改之，設r與N有關，不妨簡單設為 r(N)=r－ kN，由此得到 Logistic 模型。［1］

1．2 幾何凸性

1．2．1 幾何凸函數的概念

定義 設f(x)在區間I上有定義，如果對于任意x1那么稱f(x)是I上的幾何凸函數。

1．2．2 幾何凸函數的幾個性質

性質1 若g:(c，d)→(－∞，+∞)是連續的凸函數，則f(x)=eg(lnx)是(ec，ed)上的幾何凸函數。(證明見文獻［2］)

性質2 設(a，b)?(0，+∞)，f:(a，b)→(0，+∞)，f則當

x(f(x)f″(x) －(f′(x))2)+f(x)f′(x)≥0 時，f(x)是幾何凸函數(不等式反向時，f(x)為幾何凹函數)，反之亦然。(證明見文獻［2］)

性質3 幾何凸函數的倒數是幾何凹函數。［2］

性質4 kf(x)(k＞0)與f(x)有相同的幾何凹凸性。［3］

1．2．3 Logistic 模型的幾何凸性

Logistic模型的一般形式為:

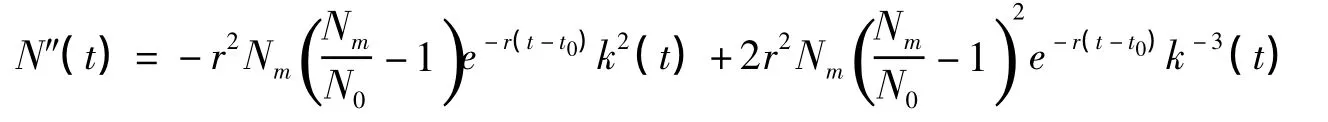
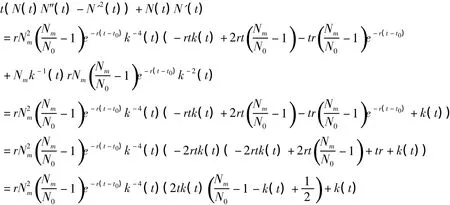
1．3 彈性［4］

1．3．1 彈性概念

f(x)的彈性是指函數的相對改變量與自變量的相對改變量的比值的極限，反映f(x)對x的變化的反應的強烈程度和靈敏度。其計算公式為:

1．3．2 彈性性質

定理 設(a，b)?(0，+∞)，f:(a，b)→(0，+∞)，f二階可導，則 f(x)是幾何凸(凹)函數的充要條件是f(x)的彈性是單調增加(減少)的。

1．3．3 Logistic 模型的彈性

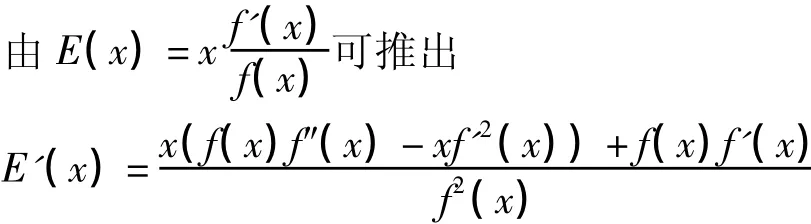
若 f(x)的彈性單調增加，則 E′(x)≥0，則 x(f(x)f″(x) －(f′(x))2)+f(x)f′(x)≥0，則 f(x)是幾何凸函數。

若 x(f(x)f″(x) － (f′(x))2)+f(x)f′(x)≥0，則 E′(x)≥0，則 f(x)的彈性單調增加。

而Logistic模型為幾何凸函數(見上面證明)，所以Logistic模型的彈性單調增加。

2．Logistic模型幾何凸性、彈性的應用

2．1 人口預測問題［5］

首先，國策之英明，解決了中國的生存大問題，試想若沒有解決好這個問題，國家談何發展，更談不上抓住機遇，為人類做出自己更大的貢獻。但是，現在的國情有所變化，那就是，人口老年化步伐越來越快，根據最近幾次的人口普查資料，發現幾乎符合Logistic模型，在這里，是凸函數，所以根據“幾何凸(凹)函數的充要條件是f(x)的彈性是單調增加(減少)的”的性質得知其彈性單調增加。彈性反映Logistic模型函數對變量時間t的變化的反應的強烈程度和靈敏度，隨著時間的推移，人口老年率將越來越大，勢必影響國家的長治久富久強，人口老年化到達一定程度，甚至連非老年人創造的財富和國家積余財富之和都將不能承受。為此，只有降低老年率，而降低老年率的有效措施就是增加非老年人，從國外輸入人口是不現實的，因為中國人口基數仍然是很大的，所以筆者認為，從現在開始可以在全國范圍內，暫時改變計劃生育政策，那就是允許國家工作人員可以生二胎，一段時間后，必將減慢老年化步伐，雖然人口總數在上漲，但只要在國家資源所能承受范圍內，還是可以執行的。(考慮到國家人口基數較大，所以現在這三十年內還不能允許生三胎。)

2．2 房價預測問題

對當前熱門話題之一——房價問題，筆者談談一些想法:根據最近幾次的房地產行情調查資料［6］，發現幾乎符合Logistic模型，如果房子需求函數符合Logistic模型，就可以利用幾何凸性與彈性的關系，即“幾何凸(凹)函數的充要條件是f(x)的彈性是單調增加(減少)的。”

如果房子供給函數符合Logistic模型，就可以利用幾何凸性與彈性的關系，即“幾何凸(凹)函數的充要條件是f(x)的彈性是單調增加(減少)的。”在這里，它是凸函數，所以彈性單調增加。所以大中城市地區房地產開發，可以采取價格遞減策略，因為該模型彈性是單調增加的，這樣供給對價格變動的反應靈敏度就大，從而就必然有不少供給者的退出開發行為發生，從而使房地產產業發展與國家的民生政策處在一個平衡點上。

［1］張學良．Malthus和Logistic模型及其醫學應用［J］．數理醫藥學雜志，2008(5)．

［2］鄭寧國．趨勢外推法數學模型的幾何凸性分析［J］．高等數學研究，2007(1)．

［3］李世杰，張小明．關于連續函數的T幾何凸性問題［J］．浙江萬里學院學報，2006(2)．

［4］黃金瑩．彈性函數的運算性質及其應用［J］．佳木斯大學學報:自然科學版，2005(1)．

［5］陳汝棟，于延榮．數學模型與數學建模［M］．北京:國防工業出版社，2006．

［6］魏巍賢，李陽．我國房地產需求的地區差異分析［J］．統計研究，2005(9):56－60．

［7］趙樹嫄，胡顯佑，陸啟良．微積分學習與考試指導［M］．北京:中國人民大學出版社，1997．