單毛細管中Ellis流體的滲流特性分析

員美娟，鄭 偉

（1.武漢科技大學冶金工業(yè)過程系統(tǒng)科學湖北省重點實驗室，湖北武漢，430065；

2.中國科學院測量與地球物理研究所大地測量與地球動力學國家重點實驗室，湖北武漢，430077）

文獻［1］～文獻［4］利用分形毛細管模型研究了幾種非牛頓流體的流動特性。Ellis流體是非牛頓流體中常見的一種。本文在考慮實際彎曲毛細管的分形特性基礎上，研究Ellis非牛頓流體在單毛細管中的流動特性，以得到其不含經(jīng)驗常數(shù)的分形表達式。

1 Ellis流體在單毛細管中流動的分形模型

1.1 流量

Ellis流體在單根毛細管中的流量方程為［5］：

式中：Δp／L0為施加在毛細管兩端的壓力梯度，其中Δp為毛細管兩端的壓降；L0為毛細管通道的直線長度；R為毛細管的半徑；φ0、φ1和α為描述Ellis流體特性的常量，其中α＞1。

當φ1＝0時，Ellis模型可簡化為牛頓模型，流體在管壁處受到的切應力τw為

彎曲毛細管通道中流體流動的分形冪規(guī)律為［6］

式中：DT為毛細管的迂曲度分形維數(shù)；Lt為彎曲毛細管通道的實際長度，且Lt≥L0。

考慮到彎曲流線的分形特征，采用毛細管的實際長度Lt，式（1）可改寫為

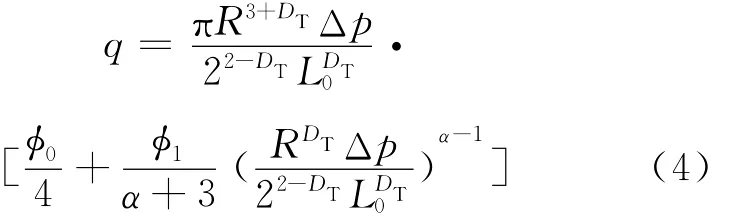
式（4）即為Ellis流體流量方程的分形表達式。式（4）中，當φ1＝0時可得單毛細管中牛頓流體流量方程的分形表達式為

由式（4）、式（5）可以看出，流量是流體特性參數(shù)、毛細管結構參數(shù)和毛細管兩端壓降的函數(shù)。

1.2 流速

由式（4）可得單毛細管中Ellis流體的流速表達式為

由式（6）可知，Ellis流體在單毛細管中的流速不僅與毛細管的半徑R和迂曲度分形維數(shù)DT有關，而且與施加在毛細管兩端的壓力梯度（Δp／L0）和流體的特性參數(shù)（φ0、φ1和α）有關。

式（6）中，當φ1＝0時，可得單毛細管中牛頓流體的流速表達式為

1.3 有效滲透率

Ellis流體的本構方程［5］為

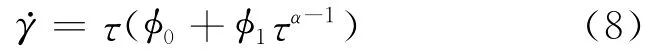
由本構方程（8）可寫出單毛細管中Ellis流體的表觀黏度μa為

管壁處的切應力τw為

結合式（6）、式（9）和式（10），由非牛頓流體滿足的廣義達西定律可得單毛細管中Ellis流體的有效滲透率為

式（11）中，當φ1＝0時可得單毛細管中牛頓流體的有效滲透率為

由式（11）和式（12）可以看出，Ellis流體的有效滲透率不僅與毛細管的結構參數(shù)有關，還與其流體特性相關；而牛頓流體的有效滲透率只與毛細管的結構參數(shù)有關，與流體特性無關。

2 結語

本文考慮到彎曲毛細管的分形特性，研究了Ellis流體在單毛細管中的流動特性，給出了該流體在單毛細管中的流量、流速和有效滲透率的分形解析解，所得結果對于進一步理解Ellis流體流動的內在物理機理有一定作用。

［1］ Yun M J，Yu B M，Cai J C.A fractal model for the starting pressure gradient for Bingham fluids in porous media［J］.International Journal of Heat and Mass Transfer，2008，51（5）：1 402－1 408.

［2］ Yun M J，Yu B M，Cai J C.Analysis of seepage characters in fractal porous media［J］.International Journal of Heat and Mass Transfer，2009，52（13）：3 272－3 278.

［3］ Yun M J，Yu B M，Xu P，et al.Fractal analysis of power－law fluid in a single capillary［J］.Chinese Physics Letters，2008，25（2）：616－619.

［4］ 員美娟，鄭偉.單毛細管中卡森流體的分形分析［J］.武漢科技大學學報，2012，35（3）：229－231.

［5］ Govier G W，Aziz K.The flow of complex mixtures in pipes［M］.New York：Litton Edu Pub Inc，1972，143－144.

［6］ Yu B M.Fractal character for tortuous streamtubes in porous media［J］.Chinese Physics Letters，2005，22（1）：158－160.