高性能圖像多級小波變換的硬件設計與實現

夏海靜，溫 彤，李其虎

(1.衡水學院 數學與計算機系，河北 衡水053000;2.上海海事大學 物流工程學院，上海201306;3.中國科學院 光電技術研究所，四川 成都610209)

自從20世紀80年代小波數學理論的誕生到現在，小波理論經歷了多個發展階段，從數學理論的建立和研究，到基于傅里葉分析形成的第一代小波的Mallat卷積算法，直至提升小波思想的引入發展出第二代小波基的構造方法，小波分析以其良好的時間頻率分析特征以及多尺度分析能力已經被廣泛地應用于圖像處理的各個領域［1-2］。針對小波分析實現方式而言，此處單從二維離散小波的數學原理角度出發，可以概括為2種方法:一種方法就是參照一維小波變換結構，構造出二維小波變換基，利用被構造的二維小波基函數直接對圖像信號進行分析，從而得出變換結果;另一種方法就是將二維圖像信號理解為由多個一維信號組合而成，采用一維信號的小波分析方法來實現數字圖像的二維小波變換［3-4］。這種方法簡單易實現，進而被廣泛采用。關于二維離散小波變換的硬件實現，目前國內外許多學者提出了許多好的結構及其硬件實現方式。例如TAN等人采用第二代提升小波結構，將圖像邊緣數據內嵌于整個算法過程中，很好地解決了圖像數據邊界擴展問題［5］。文獻［6-7］中采用的原位數據運算方式，利用圖像像素在變換過程中變化的特征規律，取得較好的效果。此外也有其他學者針對不同小波變換的硬件實現提出了不同的硬件設計方案［8-9］。

本文從小波分析的數學原理出發，在總結前人的基礎上［10-11］，以Le Gall(5/3)小波為例，設計了一種結構異常簡單，性能優良的高速圖像多級小波變換結構。該結構在圖像數據運算過程中充分考慮每個像素的運算特點，在讀取二行面陣圖像數據之后，整個變換就開始執行。該變換結構最大特點可以概括為:1)在進行二維圖像變換時，不需要等所有行(列)變換結束后，再進行列(行)變換;2)不需要某一級變換完成后再進行下一級變換。本文所設計的變換架構可以多級同時變換，進而有效地提高了變換速度，為基于小波分析圖像處理技術的高速硬件實現提供了基礎。

1 小波分析理論基礎

對于給定一個基本函數ψ(t)，令

式中:a和b均為常數，且a＞0。函數ψa，b(t)是基本函數ψ(t)先作移位再作伸縮以后得到。a和b不斷地變換，可得到一組函數ψa，b(t)。所以對于給定一個平方可積信號x(t)，即x(t)∈L2(R)，則x(t)的連續小波變換被定義為

則正變換形式為

傳統的小波變換(第一代小波)采用的都是卷積算法。典型代表為基于濾波器結構的Mallat算法，其過程復雜，用算量大，實時性差，硬件實現困難。目前工程實際進行小波變換的方法是基于提升結構的第二代小波變換。本文中基于VLSI實現的多級小波變換是JPEG2000標準中采用的Le Gall(5/3)小波，其對應的濾波器組的形式為分別代表分析端高通與低通濾波器抽頭系數。對于長度為N的一維序列，采用Mallat公式需要2N點乘法運算。利用提升算法，發現只需要N點乘法，即從乘法運算量上即可降低一半。此外通過分析該濾波器變換時的數據特征可以看出，Le Gall(5/3)提升變換過程是典型的同址、原位運算過程。

2 Le Gall(5/3)提升小波原理

Le Gall(5/3)小波正向變換過程的數學表達式為

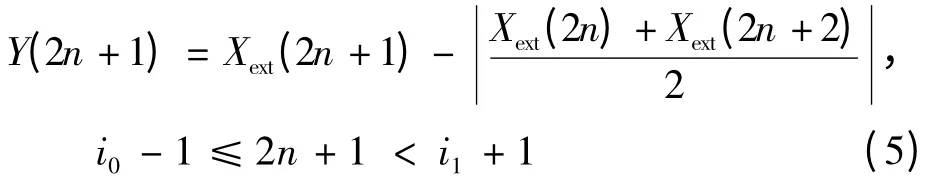
式中:Y是一維信號X的變換結果。其中，Xext(n)是一維信號X的對稱周期擴展，i0和i1分別是X第一個樣本和最后一個樣本的序號。由上一節可知，在進行信號的提升變換過程中，通常要經過分裂、預測和更新這3個步驟。一維Le Gall(5/3)小波提升架構如圖1所示，在輸入端，將信號進行奇偶分裂，用偶數項來預測奇數項，再用預測后的奇數項來更新偶數項，從而實現一維一級提升。

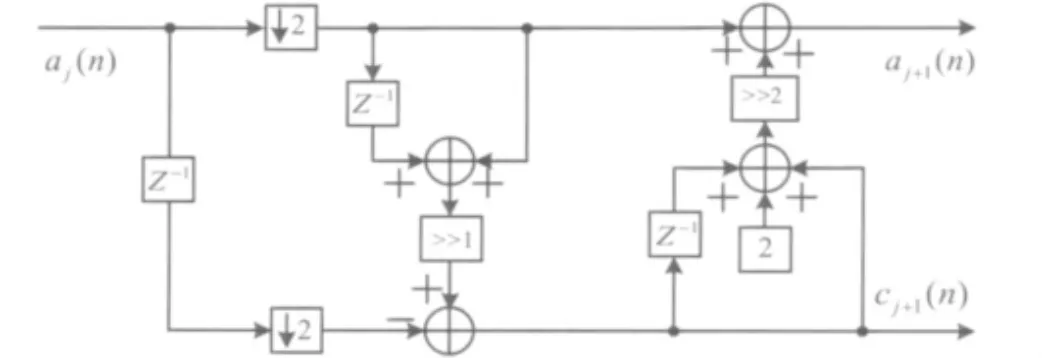
圖1 Le Gall(5/3)小波提升硬件實現架構

通過分析(5/3)小波提升架構可知，在提升過程中，分裂僅僅是一個概念，在實際運算過程中并不是必需的。計算過程中只要能確定哪些是奇數項、哪些是偶數項即可。圖1中2倍下采樣表示將原始信號分解為2個奇數項和偶數項。在硬件實現時，通過奇偶選擇信號，將奇偶項分開。奇偶信號分別用不同的信號端口輸出，此時時鐘頻率降為原始數據時鐘的一半。將偶數項信號延遲后相加，再經過移位除法器后與相對應的奇數項相減，來預測奇數項值，之后通過延遲環節將得到的2項預測值來更新奇數項。

值得注意的是，在一維信號長度為0～N-1的起始端和結束端運算時，信號要進行邊界延拓，上述內容里已經提到多種邊界延拓方式，在實際硬件運算過程中，由于傳統方法一般采用周期對稱拷貝邊界數據或是通過地址轉換將延拓部分數據映射到原始數據上。這2種方法需求內存較多，且功耗較大。為此本設計在結構上采用了改進的內嵌延拓提升［5］方法以解決邊界周期延拓問題，具體做法為:當判斷信號為最左端起始信號時，對x(0)進行更新操作，由于缺乏左邊預測項，所以此時的更新公式變為式(7);當判斷信號為最右邊時，對x(N-1)進行預測操作，由于缺乏右邊的預測項，則此時的預測公式變為式(8)。其他情況下，由于不需要進行數據延拓，則按照正常提升方式進行。內嵌延拓提升將原來統一計算流程分成3個階段，分別為起始階段、長時間正常運行階段和結束階段，所以在變換時需要加一個計數器以判斷一行的起始和末尾。針對二維圖像信號還需要加上一個計數器來判斷起始行和末尾行。式(7)和式(8)為

3 二維提升小波變換的硬件實現

3.1 一級二維小波提升硬件實現

為檢驗上述設計思想的正確性，在Xilinx公司的ISE10.1.3開發環境下，采用VHDL語言開發了上述一維5/3整數小波正向變換過程。為便于層次化設計，結構采用模塊化設計，其模塊接口如圖2所示。輸入端口包括輸入數據Data_in、輸入數據有效性In_valid、輸入數據時鐘頻率Clock_in、輸入數據的二分頻時鐘Clock_in/2，以及整個模塊的復位信號Reset。輸出端口包括低頻信號輸出部分Data_L、高頻信號輸出部分Data_H以及輸出信號是否為效信號Out_valid。

圖2 1D Le Gall 5/3小波變換外圍接口圖

為證明該結構的功能正確性，圖3為該結構對一組長度為12的一維信號進行一級變換后，得到的輸入輸出數據值。從波形圖中可以看出，從原始數據輸入到輸出需要經過10個時鐘周期的延遲。在Xilinx公司的XC5VFX70T(-3)型號FPGA下進行綜合時鐘頻率高達399.76 MHz。該結構的正確、高效設計為高速二維圖像信號的小波變換的硬件實現做好了前期準備。

圖3 軟件功能仿真5/3小波變換波形圖

在對分辨力為M×N圖像進行二維小波硬件提升時，圖像以偶數行開始，奇數行結束，在第0行和第M-1行時，由于缺少前一行緩存數據對偶數行進行更新，缺少第M行對第M-1行進行預測，所以列變換時，同樣進行列變換內嵌延拓。當對第0行進行更新時，更新公式表示為式(9)，當對最后一行進行預測時，采用式(10)進行預測。式(9)和式(10)為

為便于層次化設計，二維5/3小波變換硬件結構同樣采用了模塊化設計，其模塊接口如圖4所示，與一維變換模塊不同的是，輸入端采用幀信號與行信號來決定輸入端數據Data_in是否有效。輸出端共有6個輸出端口，每一個子帶都分別對應一個輸出信號，分別為LL_T，LH_T，HL_T和HH_T。另外輸出端利用輸出幀有效性信號Fval_out和輸出行有效信號Lavl_out來決定輸出信號是否有效。

圖4 2D 5/3小波變換外圍接口圖

為驗證上述架構的正確性，在Xilinx公司的XC5VFX70T(-3)型號FPGA中，開發上述二維小波提升架構，最終綜合后時鐘頻率可達387.597 MHz，為檢驗硬件變換后的結果與理論值是否一致，在FPGA中通過模擬一幅二維圖像，圖像每行都是0～399共400個數據，將模擬的圖像數據輸入到二維5/3變換模塊，輸出值通過Chipscope進行數據觀察，輸出波形圖如圖5所示，完全符合理論計算值，進而進一步驗證了本結構設計的正確性。

圖5 一級二維5/3小波VLSI變換波形

3.2 多級二維小波變換的硬件實現

本文中所提的多級二維小波變換同樣是采用級聯單級二維小波變換模塊來實現，級聯的單級模塊為3.1節中所設計的模塊結構。具體按照式(11)進行步步級聯從而實現多級變換。

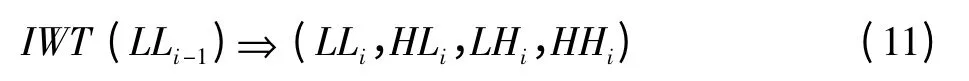
不同變換級與級之間遞歸級聯結構如圖6所示。某一級變換后的數據都需要存入一個FIFO，該FIFO的長度至少為下一級變換的一行數據長度。當某一級變換的最低頻數據存滿一個FIFO后，控制程序會將該FIFO中的數據順序讀出，送入下一級變換模塊，并相應的輸出4個子帶。值得注意的是，該結構不同變換級之間采用FIFO進行緩存后再輸入到下一個變換模塊中，而不是將某一級最低頻子帶有數據就送入下一級中。這樣做的目的主要有:1)使得整個多級變換模塊的流水線更短，硬件變換效率更高;2)使得整個多級變換模塊時鐘同步，所有模塊都使用相同的時鐘去控制，進而使得整個模塊控制起來更加簡單。

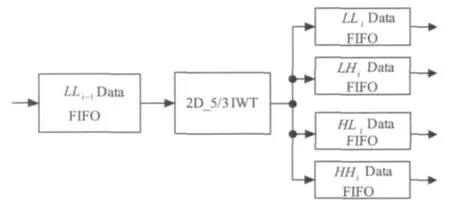
圖6 不同變換級之間結構

二維多級變換硬件設計時，系統共有2種時鐘，其中一種時鐘是圖像像素的輸入時鐘Clock，當每行的數據值從外部輸入到內部之后，首先經過分裂器將數據的奇偶分裂開，這時1行數據相當于2行數據，而每行的數據輸入頻率為原始數據輸入頻率的一半，即Clock/2，之后這2行數據分別經過預測器和更新器所需要的時鐘頻率都為原始數據時鐘頻率的一半。最后的數據輸出到外部各自的FIFO中的寫時鐘都為Clock/2。此外由于每級變換后的數據都有延遲，所以每一級的輸出數據除了具有4個子帶數據之外，還需要有輸出的幀信號與行信號，以便給下一級變換模塊使用。當一幀數據變換完成后，系統需要進行復位操作。此外通過分析可知，整個硬件系統中沒有任何關于數據地址的操作，即只對變換數據進行移位和存儲，從而使得整個系統變得更加簡單、易操作。

基于不同變換級結構，以及在前面的二維變換模塊的基礎，筆者設計了多級二維小波變換的級聯遞歸總體結構框架，如圖7所示，該架構可以為實現任何級數小波變換提供硬件架構基礎。圖中共級聯了N個單級二維小波變換遞歸單元。每一個級聯單元雖然都工作在同一個時鐘頻率下，但是每一級內部又都具有各自的獨立性。每一單級小波變換后的數據輸出都是連接到各自的FIFO中，除某些低頻小波子帶FIFO輸出端口接到下一級變換碼塊中以外，所有的子帶FIFO輸出端都連接到一個多路數據選擇器中，多路選擇器根據每一級小波子帶系數的出現規律，有規則地將各級各子帶的小波子帶系數輸出到后端，供后續圖像處理或傳輸使用。

本文基于上述多級二維小波變換級聯遞歸總體結構框架，對各個模塊采用VHDL語言進行程序化設計。利用2款Xilinx公司不同型號FPGA，分別為XC2VP30-FF1152(-6)和XC5VFX70T-FF1136(-3)，進行實際測試，三級二維5/3小波變換在不同器件下資源消耗比例以及綜合后時鐘頻率值如表1所示。從表中可以看出在XC2VP30-FF1152(-6)中，FPGA數據吞吐率能達183 Msymbol/s(兆符號/秒)。利用XC5VFX70T-FF1136(-3)可實現387 Msymbol/s數據吞吐率，而資源消耗最多的內部BRAM則僅僅為整個硬件資源的10%。

表1 2款硬件資源消耗比例表

4 總結

本文在研究小波分析的數學原理基礎上，以Le Gall(5/3)小波為例，分析該小波在進行二維圖像提升變換時，每個像素值的運算規律，設計并實現了一種高性能的多級二維小波變換，該小波在對圖像進行多級變換時硬件最大的特點有:1)不需要進行傳統的行變換之后，再進行列變換，而是采取了行、列同時變換的方式進行;2)在多級變換時，傳統變換模式是一級變換完成后才能變換下一級，本文采用的是不同級之間同時變換的方式。最后在硬件電路中，利用VHDL語言完成整個變換架構的設計。實驗結果證實本文所設計的多級二維小波變換的硬件實現方式符合理論計算值，從而為基于小波分析的圖像處理技術高速硬件實現奠定了基礎，具有較高的理論意義與工程應用價值。

［1］SWELDENS W.The lifting scheme:a construction of second generation wavelets［J］.SIAM Journal on Mathematical Analysis，1997，29(2):511-546.

［2］JIANG W，ORTEGA A.Lifting factorization based discrete wavelet transform architecture design［J］.IEEE Trans.Circuits and Systems of Video Technology，2001，11(5):651-657.

［3］DAUBECHIES I.The wavelet transform，time-frequency localization and signal analysis［J］.IEEE Trans.Information Theory，1990，36(5):991-1006.

［4］MALLAT S G.A theory for multiresolution signal decompostion:the wavelet representation［J］.IEEE Trans.PAMI，1989，11(7):673-693.

［5］TAN K C B.Low power embedded extension algorithm for lifting based discrete wavelet transform in JPEG 2000［J］.Electronics Letters，2001，37(25):1328-1330.

［6］顏學龍，余君.二維離散小波變換的FPGA實現［J］.電視技術，2007，31(4):19-21.

［7］康志偉，顏福權.基于提升算法的二維DWT高效VLSI實現結構［J］.國防科技大學學報，2005，27(6):48-52.

［8］林路音.JPEG2000中提升小波算法的FPGA實現［D］.哈爾濱:哈爾濱工業大學，2006.

［9］LIAO H，MANDAL M K，COCKURN B F.Efficient architectures for 1-D and 2-D lifting based wavelet transform［J］.IEEE Trans.Signal Processing，2004，52(5):1315-1326.

［10］ANDRA K，CHAKRABARTI C，ACHARYA T.A VLSI architecture for lifting-based forward and inverse wavelet transform［J］.IEEE Trans.Signal Processing，2002，50(4):966-977.

［11］LINA C J，CHEN K F.Lifting based discrete wavelet transform architecture for JPEG2000［C］//Proc.2001 IEEE International Symposium on Circuits and System(ISIC-2001).Singapore:［s.n.］，2001:497-500.