圖像的超小波稀疏表示

李春華，秦志英

(河北科技大學a.信息科學與工程學院;b.機械電子與工程學院，河北 石家莊050018)

圖像稀疏表示旨在確保圖像精度的前提下，用數量最少的基函數組合近似表示圖像，使圖像的特征用盡量少的變換系數表達出來，在圖像壓縮、特征提取、圖像檢索、圖像去噪和圖像復原等應用中具有重要作用。Vinje和Gallant通過生理學的實驗顯示［1］，主視覺皮層的神經元在接受自然圖像作為輸入刺激時，其響應是滿足稀疏性的，證實了圖像稀疏表示模型能夠有效匹配人類的視覺感知特性。

Mallat和Zhang將Coimfan和Wickerhauesr等提出的信號稀疏分解概念推廣到圖像處理領域［2-3］。在圖像稀疏表示中，基函數的選擇是關鍵。基函數與圖像信號的結構越匹配，越容易形成圖像的稀疏表示。隨著多尺度幾何分析的興起，出現了Ridgelet，Curvelet，Contourlet，Wedgelet等一系列圖像稀疏表示的超小波方法。它們放寬了正交基表示圖像的嚴格條件限制，采用框架(超完備基)來表示圖像，獲得更好的圖像表示效果。本文針對Fourier變換和小波變換用于圖像表示應用存在的不足，研究了各種新興起的超小波變換稀疏表示圖像的方法，分析了它們各自的特點與優勢，并對未來發展進行了展望。

1 Fourier變換和小波變換表示圖像存在的問題

經典的Fourier變換可以對平穩信號形成最優表示，但表示圖像這種非平穩信號時，只能把圖像分解成具有不同強度和不同頻率的分量組合，而不能同時表示出頻率分量在圖像上出現的位置，喪失了圖像的空間分析特性。小波基具有良好的空間-頻率局部化特性，較好地解決了Fourier變換在時域分析和頻域分析之間的矛盾，被靜止圖像編碼新標準JPEG2000選用。但是圖像表示通常采用二維可分離小波基，基函數各向同性，只能有效表示零維奇異點。這是因為二維可分離小波基是由一維小波基通過張量積的方式推廣得到的，支撐區間在不同分辨力下，表現為不同尺寸大小的正方形，不具有各向異性特征。它在表示圖像邊緣時，相當于用一系列的“點”去捕捉圖像中的“線”。這種維度的差異嚴重影響了小波的逼近效率，導致在邊緣輪廓處聚集了大量的大幅度小波系數。而且可分離二維小波變換在表示圖像時，只能表達出水平、垂直和對角3個方向的圖像信息，不利于完整表達自然圖像［4］。為了克服實數小波變換的時移敏感性和方向性缺乏的缺陷，Kingsbury提出了復數小波稀疏表示圖像的方法［4］，用兩個實數濾波器分別近似逼近復小波的實部和虛部，具有近似的平移不變性和更多的方向選擇性。復小波變換采用雙樹結構，一樹生成變換的實部，一樹生成虛部［4-5］，變換后產生了6個方向的高頻子圖像，分別指向±15°，±45°，±75°。但是分析方向數目還是無法滿足自然圖像角度分辨力的要求。由此看來，小波變換只能最優描述零維奇異目標函數，表示二維或更高維奇異性信號存在明顯缺陷。

2 超小波圖像稀疏表達方法

最近幾年，出現了一些新的圖像變換表示方法:如脊波(Ridgelet)、曲波(Curvelet)、輪廓波(Contourlet)、線波(Beamlet)、楔波(Wedgelet)、板波(Platelet)等。這些方法的基本思想是為了使基函數能更好地表現圖像特征，放寬了對基函數的正交性要求，改用一組超完備的框架基作為圖像稀疏表示的原子。事實證明，基于超小波變換的圖像表示方法可以更加稀疏地表示圖像。

超小波關注如何表達圖像的不連續性(或奇異性)，沿襲小波的理論模式，構造出一些列能夠多分辨力表達圖像的“基”或“標架”，這些超小波的母函數具有各向異性的特點，通過靈活地調整基的方向和支撐區間的形狀，可以用較少的系數快速有效地捕捉圖像的奇異信息。它們具有下列共同特點:

1)具有幾何規則性，能夠逼近圖像中任意方向的線、曲線的不連續性;

2)有容易計算的分析(正變換)和綜合(反變換)表達;

3)對分析(變換)域的結果有明確的物理解釋，便于實施去噪、壓縮的近似處理，以及超分辨重建的進一步工作。

2.1 Ridgelet變換與Curvelet變換

脊波理論由Emmanuel J Candes在1998年提出［6］，一個典型的Ridgelet母函數如圖1所示，具有各向異性的特點。小波變換是逐點刻畫點的奇異性，而Ridgelet變換是沿脊線刻畫線的奇異性。因此，Ridgelet變換在方向選擇和識別方面，比小波變換性能優越，可以更有效地表示信號的一維方向奇異特征。

用脊波作為基函數來檢測直線特征，可以有效地捕獲各個尺度、各個位置和各個方向上的信息，逼近直線型奇異函數具有優越性。然而自然圖像的邊緣不一定都是直線型的，脊波變換不能很好地處理曲線奇異性，這樣脊波變換就滿足不了要求。

圖1 Ridgelet母函數

為了表示圖像中的曲線奇異性，文獻［7］提出了單尺度脊波變換，把圖像固定尺度均勻剖分，每個剖分塊中的曲線近似看作直線。在剖分塊中，再對每個分塊進行脊波變換。單尺度Ridgelet變換巧妙地將曲線奇異轉化為直線奇異來處理。

以單尺度Ridgelet變換為基礎，E.J.Candes和D.L.Donoho構造了多尺度Ridgelet，也就是第一代Curvelets變換［8］。第一代Curvelet先對圖像作小波變換，然后對不同尺度的子帶圖像采用不同大小的尺寸分塊后進行脊波變換。Curvelets變換能在所有可能的尺度上進行Ridgelet變換，克服了單尺度脊波變換固定尺度的缺陷，對曲線狀奇異特征具有稀疏表示的能力。

但是Curvelet變換存在數字實現復雜、數據冗余量巨大的缺陷。而且，由于Curvelet變換是基于塊剖分的變換，重構圖像中存在塊邊界效應。為了解決這一問題，需要預先對各剖分塊進行疊加處理。這樣不僅運算復雜度增大，還加大了變換系數的冗余度。于是，Candes等人又提出了實現更簡單、更便于理解的第二代Curvelet變換［9］。定義徑向窗函數W(r)和角度窗函數V(t)，它們滿足可允許條件

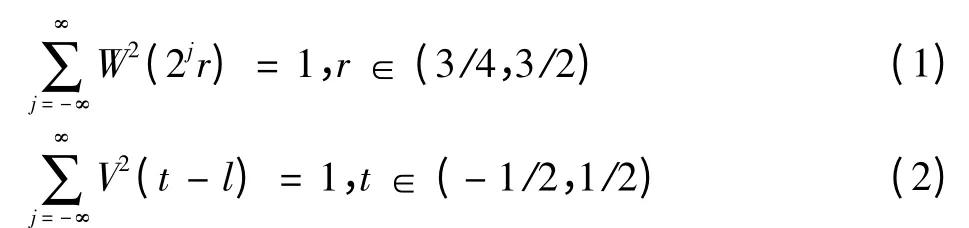
對于每一個j≥j0，定義傅里葉頻率的頻率窗:Uj(r，，其中?」表示下取整，Uj的支撐區間是受W和V支撐區間限制獲得的楔形區域，方向數目隨尺度隔層加倍。對應的時域支撐區域具有各向異性，如圖2所示。Curvelet變換能用極少的非零系數精確表達圖像邊緣，可以在確保低均方誤差的約束下，實現圖像表示數據精簡性與精確性的平衡。

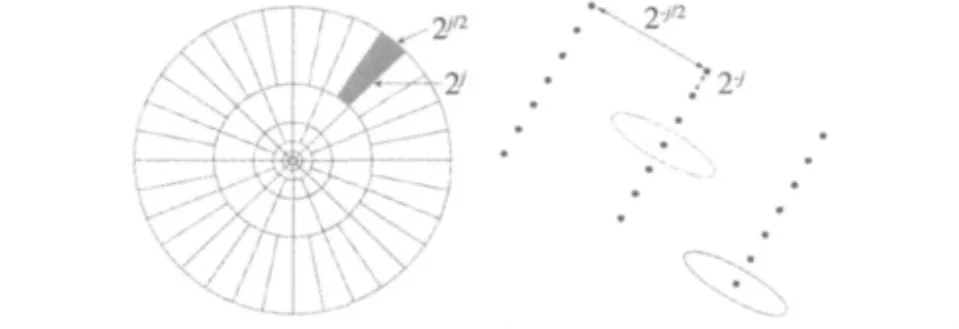
圖2 Curvelet變換

2.2 Contourlet變換與Shearlet變換

鑒于Curvelet變換是一種頻率定義的方法，導致笛卡兒坐標與極坐標間轉換需要插值計算。M.N.Do和Martin Vetterli直接從離散時間域提出一種與Curvelet類似的方向性多分辨變換——Contourlet變換［10］，更適合數字圖像表示。

Contourlet變換作為Curvelet變換的另一種快速數字實現方式，繼承了Curvelet變換支撐區間各向異性的多尺度關系特點。如圖3所示，它將多尺度分析和方向分析分拆進行，首先用拉普拉斯塔形分解方法搜索邊緣奇異點，再用方向濾波器組將位置相近的奇異點集結成輪廓線段。Contourlet變換基的支撐區間是“長條形”結構，其長寬比隨尺度變化，如圖4所示。Contourlet表示圖像邊緣的系數能量更加集中，對于曲線有更“稀疏”的表達。圖5、圖6分別為小波變換和Contourlet變換用相同數量的系數重建圖像的效果。

2007年，Guo和Labate等人提出了一種新的接近最優的多維函數表示方法——剪切波(Shearlet)變換［11］。相對于輪廓波變換來說，Shearlet變換具有完備的理論和數學基礎，它與小波變換類似，通過一個基本函數的膨脹、剪切和平移變換來構造基函數，可以在廣義多分辨分析的框架下進行研究，它在頻率空間沿斜率方向逐層加倍細分，并且對剪切操作在方向數目上沒有限制。Shearlet變換是一種更為靈活的數字圖像表示方法，可以對圖像進行靈活的多分辨和多方向分解，對圖像中的邊緣和紋理等細節信息給出接近最優的性能表示。

2.3 Beamlet變換與Wedgelet變換

為了確定圖像中線段的端點及長度信息，Donoho提出了連續Beamlet變換及其在多尺度分析中的應用［12］，Xiaoming Huo提出了離散Beamlet變換［13］。在文獻［14］中，Donoho用Beamlet分析的理論框架將Beamlet變換和Wedgelet變換統一為Beamlet多尺度幾何分析理論。

在n×n的二進方塊內連接邊界上任意兩個像素點就構成了一條離散小線基，基上的像素點可通過插值法確定。各種方向、尺度和位置的小線基的集合形成小線庫。數字圖像在一條小線基上的離散Beamlet變換，就是這條小線基上各像素灰度值的和。Beamlet變換對線定位精確、簡單易行，變換系數以金字塔方式組織，從而實現多尺度分析。

Donoho進而提出了Wedgelet變換，與Beamlet變換結合，使用多尺度Wedgelet基對圖像輪廓進行分段線性近似［15］。一個圖像子塊借助一條分割線分成兩個楔塊，每一個楔塊用唯一的特征值表示。Wedgelet變換使用線的位置、兩個楔塊的特征值近似描述了這個子塊的性質。

在應用中先利用Beamlet詞典生成Beamlet基，Wedgelet基在Beamlet基的基礎上生成。在Wedgelet變換中，圖像中的邊緣用所選取的最優Beamlet基來分段近似表示。

3 結論

自然圖像是包含多種形態結構成分(Morphological Diversity)的復雜信號，而現在常用的傅里葉變換和小波變換無法最優地表達圖像中各種類型的結構。本文針對傅里葉變換和小波變換稀疏表示圖像存在的問題，較為全面地分析了近來新出現的各種超小波表示圖像方法。超小波建立在冗余框架下，用過完備字典分解圖像。基的種類和個數有所增加，便于表示圖像中的各種幾何結構，如邊緣、輪廓、角點、紋理等，為圖像稀疏表示提供了更好的選擇。

從圖像稀疏表示的發展進程來看，圖像表示的基函數經歷了從非冗余的正交基到適度冗余的緊框架變遷，正在向過完備字典演進。過完備字典放棄了正交性約束，能夠凸顯圖像中有意義的局部特征，更好地抵御噪聲干擾。

［1］VINJE W E，GALLANT J L.Sparse coding and decorrelation in primary visual cortex during natural vision［J］.Science，2000，287(5456):1273-1276.

［2］COIFMAN R R，WICKERHAUSE M V.Entropy-based algorithms for best basis selection［J］.IEEE Trans.Information Theory，1992，38(2):713-718.

［3］BERGEAUD F，MALLAT S.Matching pursuit of imgaes［C］//Proc.International Conference on Image Processing.［S.l.］:IEEE Press，1995，1:53-56.

［4］KINGSBURY N.Image processing with complex wavelets［J］.Phil.Trans.Roy.Soc.Lond.A.，1999，357(1760):2543-2560.

［5］KINGSBURY N.The dual-tree complex wavelet transform:a new efficient tool for image restoration and enhancement［C］//Proc.European Signal Processing Conf.Rhodes:EURASIP Press，1998:319-322.

［6］CANDES E J，DONOHO D L.Ridgelets:a key to higher-dimensional intermittency?［J］.Phil.Trans.R.Soc.Lond.A.，1999，357(1760):2495-2509.

［7］CANDES E J.Ridgelets and the representation of mutilated Sobolev functions［J］.SIAM Journal on Mathematical Analysis，2001，33(2):347-368.

［8］CANDES E J，DONOHO D L，Curvelets:A surprisingly effective nonadaptive representation for objects with edges［R］.USA:Department of Statistics，Stanford University，2000.

［9］CANDES E J，DEMANET L，DONOHO D，et al.Fast discrete curvelet transforms［J］.Multiscale Modeling Simulation，2006，5(3):861-899.

［10］DO M N，VETTERLI M.The contourlet transform:an efficient directional multiresolution image representation［J］.IEEE Trans.Image Processing，2005，14(12):2091-2106.

［11］GUO K，LABATE D.Optimally sparse multidimensional representation using shearlets［J］.SIAM Journal on Mathematical Analysis，2007，39(1):298-318.

［12］HUO Xiaoming.Sparse image representation via combined transforms［D］.Stanford:Stanford University，1999.

［13］HUO Xiaoming，CHEN Jihong.JBEAM:multiscale curve coding via beamlets［J］.IEEE Trans.Image Processing，2005，14(11):1665-1677.

［14］DONOHO D L，HUO Xiaoming.Beamlets and multiscale image analysis［M］.Berlin:Springer Press，2001.

［15］DONOHO D L.Wedgelet:Nearly minimax estimation of edges［J］.Annuals of Statistics，1999，27(3):859-897.