一類廣義Stein方程的正定解

段雪峰， 王卿文， 常海霞

(1.桂林電子科技大學數學與計算科學學院，廣西桂林541004;2.上海大學理學院，上海200444; 3.上海金融學院應用數學系，上海201209)

矩陣方程的來源和應用相當廣泛，包含于系統與控制理論、結構設計、參數識別及動態規劃等許多科學與工程計算領域［1-5］，已成為數值代數研究中的熱點問題之一.本工作研究矩陣方程

的正定解，其中A1，A2，…，Am均為n×n階非奇異矩陣，Q為n×n階正定矩陣，m為正整數.

矩陣方程(1)在m=1時就是著名的Stein方程，該方程在系統與控制理論中起著很重要的作用，許多學者對該方程進行了系統研究［1-2，5］.當m＞1時，稱該方程為廣義Stein方程，它來源于求解一類插值問題［6］，目前對于該矩陣方程的正定解的研究成果較少.本工作首次利用Thompson度量研究矩陣方程(1)，給出該矩陣方程存在正定解的充分條件;構造求其正定解的迭代方法，并給出迭代方法的誤差估計式;最后，用數值例子驗證了該迭代方法的可行性.

用P(n)表示由n×n階正定矩陣組成的集合.對于Hermitian矩陣M和N，M≥0(M＞0)表示M為半正定(正定)矩陣，M≥N表示M－N是半正定(正定)的.對于n×n階正定矩陣M，分別用λ1(M)和λn(M)表示M的最大和最小特征值.‖M‖表示矩陣M的譜范數.在錐P(n)上定義Thompson度量

1 主要結果

下面給出廣義Stein方程(1)存在正定解的充分條件，構造求解的迭代方法，并給出迭代方法的誤差估計式.

引理1［9］對任意的A，B，C，D∈P(n)，有d(A+B，C+D)≤max{d(A，C)，d(B，D)}.

引理2［10］設A是n×n階半正定矩陣，有

式中，γ=max{λ1(X)，λ1(Y)}，β=λn(A).

引理3［11］設δ(·，·)為非空集合Ω上的一個度量.如果φ是Ω上的壓縮映射，且壓縮系數為α，則映射 φ在Ω上有唯一的不動點 x*.對任意x0∈Ω，由迭代公式xm+1=φ(xm)，m=0，1，…產生的序列{xm}收斂于x*，且有如下誤差估計式：

對?X(0)∈［αI，βI］，由迭代方法

產生的矩陣序列{Xk}收斂于，且有如下誤差估計式：

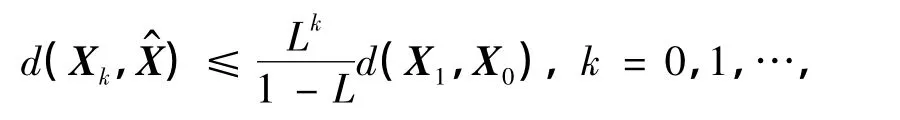
式中，

證明 定義映射

其中Ω={X：αI≤X≤βI}.顯然，Ω為一個非空閉凸集，且映射G在Ω上連續.

對任意的X∈Ω，有

又由定理的條件和式(4)和(5)，可得

即

從而

由式(7)和(8)，可得

式(9)說明映射G將Ω映射成自身.下證G為Ω上的壓縮映射.

對?X，Y∈Ω，設

則由Weyl定理，可得

又由引理1和引理2以及式(2)和(3)，可得

又因為Q為正定矩陣，則λn(Q)＞0，所以

因此，映射G在Ω上為壓縮映射.由引理3可知，映射G在Ω上存在唯一不動點，即

產生的矩陣序列{Xk}收斂于，且有如下誤差估計式：

2 數值例子

下面用數值例子來說明用迭代方法(見式(6))來求廣義Stein方程(1)的正定解是可行的.以下結果都是用Matlab 7.1軟件運行得到的.

例1 對于廣義Stein方程(1)，取m=2，

經驗證，上述A1，A2滿足定理1的條件.考慮迭代法(見式(6))，若取X0=5I，經過53步迭代后，得到廣義Stein方程(1)的正定解為

例2 對于廣義Stein方程(1)，取m=2，

經驗證，上述A1，A2滿足定理1的條件.考慮迭代法(見式(6))，若取X0=2I，經過71步迭代后，得到廣義Stein方程(1)的正定解為

例1和例2均表明用迭代法(見式(6))求廣義Stein方程(1)的正定解是可行的.

［1］ GAJICZ.Lyapunov matrix equation in system stability and control［M］.New York：Academic Press，1995：86-128.

［2］ HEINENJ.A technique for solving the extended discrete Lyapunov matrix equation［J］.IEEE Transactions on Automatic Control，1972，17(2)：156-157.

［3］ IVANOVI G，HASANOVV I，UNLIGF.Improved methods and starting values to solve the matrix equation X±A*X－1A=I iteratively［J］.Math Comp，2004，74 (6)：263-278.

［4］ RANA C M，REURINGSM C B.The symmetric linear matrix equation［J］.Electronic JournalofLinear Algebra，2002，9(16)：93-107.

［5］ SILVAF C，SIMOESR.On the Lyapunov and Stein equations［J］.Linear Algebra Appl，2007，15(8)：329-338.

［6］ SAKGNOVICH L A. Interpolation theory and its applications ［M］. Dordrecht： Kluwer Academic Publishers，1997：36-49.

［7］ NUSSBAUMR D.Hilbert’s projective metric and iterated nonlinear maps［J］.Memoirs of Amer Math Soc，1988，39：11-26.

［8］ THOMPSONA C.On certain contraction mappings in a partially ordered vector space［J］.Pro Amer Math Soc，1963，14(5)：438-443.

［10］ LEEH，LIMY.Invariant metrics，contractions and nonlinear matrix equations［J］.Nonlinearity，2008，21 (2)：857-878.

［11］ KANTOROVICHL V，AKILOVG P.Function analysis［M］.Elmsford：Pergamon Press，1982：335-361.