非均勻地應(yīng)力下套管偏心對(duì)抗擠強(qiáng)度的影響

陳占鋒， 朱衛(wèi)平， 狄勤豐， 唐繼平， 梁紅軍

(1.上海大學(xué)上海市應(yīng)用數(shù)學(xué)和力學(xué)研究所，上海200072;2.上海市力學(xué)在能源工程中的應(yīng)用重點(diǎn)實(shí)驗(yàn)室，上海200072; 3.塔里木油田公司，新疆庫爾勒841000)

目前的套管設(shè)計(jì)大多假設(shè)套管居中，即套管在井眼中的偏心度為0.這種假設(shè)在地層穩(wěn)定時(shí)不會(huì)引起復(fù)雜問題，但在鹽膏層地層中，則可能出現(xiàn)復(fù)雜情況［1-4］.塔里木油田英買力區(qū)塊鹽膏層井段的技術(shù)套管就出現(xiàn)了因密度下降導(dǎo)致的變形問題，造成鉆頭難以通過.這種情況出現(xiàn)在鉆井液密度下降至1.25 g/cm3時(shí)，而按常規(guī)方法計(jì)算，該條件下套管的抗擠強(qiáng)度尚有余量.研究表明，當(dāng)套管的抗擠強(qiáng)度余量較小時(shí)，套管居中時(shí)的強(qiáng)度雖能滿足要求，但當(dāng)套管偏心一定量后，套管抗擠強(qiáng)度就可能得不到滿足.塔里木油田英買力區(qū)塊鉆進(jìn)過程中出現(xiàn)的套管變形問題，正是這一原因所致.事實(shí)上，套管居中能有效改善套管的受力狀況，抵抗更大的地應(yīng)力.但在實(shí)際井眼中，由于井斜角的存在、扶正器的位置不當(dāng)?shù)仍颍沟锰坠懿⒉荒芤恢碧幵谒喹h(huán)的正中央［5-7］.很多學(xué)者已經(jīng)認(rèn)識(shí)到套管偏心對(duì)套管抗擠強(qiáng)度的影響，并開展了不少相關(guān)的工作［8-11］，但專門分析非均勻地應(yīng)力下套管偏心對(duì)套管抗擠強(qiáng)度的影響的研究還未見相關(guān)報(bào)道.本研究采用有限元法，建立了套管-水泥環(huán)-地層耦合模型，對(duì)固井過程中的套管偏心現(xiàn)象，以及套管偏心對(duì)套管抗擠強(qiáng)度的影響進(jìn)行了分析.

1 套管偏心的有限元模型及計(jì)算參數(shù)

在井眼中心建立坐標(biāo)系XOY，設(shè)套管中心為點(diǎn)O'，井眼半徑為 R，套管外徑為 r，偏心距 OO'= ρ(ρ∈［0，R－r))，將OO'與X軸的夾角定義為偏心方位角φ(φ∈［0°，360°)).當(dāng)［ρ，φ］取不同值時(shí)，即可描述套管不同的偏心特征，如圖1所示.

圖1 受力示意圖Fig.1 Force schematic diagram

采用笛卡爾直角坐標(biāo)系，設(shè)Z軸與套管軸線重合，且為地應(yīng)力的3個(gè)主軸之一，其余2個(gè)應(yīng)力主軸分別對(duì)應(yīng)X軸和Y軸(見圖1).可以認(rèn)為，在一定范圍內(nèi)，整個(gè)系統(tǒng)沿套管長(zhǎng)度(Z軸)方向的力學(xué)量基本不變.因此，根據(jù)彈性理論，可將該問題看作平面應(yīng)變問題，平面范圍取井徑尺寸的5倍以上，以消除邊界效應(yīng)對(duì)套管應(yīng)力的影響.假設(shè)套管-水泥環(huán)-地層的交界面膠結(jié)良好，且緊密地連接在一起，所建立的套管-水泥環(huán)-地層模型如圖2所示.單元類型選取8節(jié)點(diǎn)Plane183四邊形單元，按內(nèi)密外疏的方式劃分網(wǎng)格.根據(jù)塔里木油田的實(shí)際情況，選取P110套管作為研究對(duì)象，套管內(nèi)半徑r0=109.52 mm，套管外半徑r=125.4 mm，井眼半徑R=155.6 mm，其他計(jì)算參數(shù)如表1所示.

圖2 有限元模型Fig.2 Finite element model

表1 套管、水泥環(huán)和地層材料的基本參數(shù)Table 1 Basic parameter of casing，cement sheath and formation

2 計(jì)算結(jié)果

根據(jù)塔里木油田的實(shí)際情況，取鉆井液密度為1.25 g/cm3，井深為4 995 m.對(duì)最大地應(yīng)力σH= 140 MPa，最小地應(yīng)力σh=134 MPa時(shí)的套管工況進(jìn)行研究.計(jì)算時(shí)套管內(nèi)壓為Pi=61.25 MPa，X方向?yàn)樽畲蟮貞?yīng)力方向，Y方向?yàn)樽钚〉貞?yīng)力方向.分別計(jì)算當(dāng)偏心距為ρ=2.5，5.0，…，20.0 mm，偏心方位角為φ=0°，10°，…，180°時(shí)，套管的von Mises應(yīng)力分布及最大von Mises應(yīng)力值σmax.

圖3為套管偏心與套管最大von Mises應(yīng)力的對(duì)應(yīng)關(guān)系圖，圖中曲面表示套管在對(duì)應(yīng)偏心下的最大von Mises應(yīng)力.可以看出，當(dāng)套管偏心方位角為0°和180°時(shí)，套管的最大應(yīng)力隨偏心距的增大逐漸減小;當(dāng)套管偏心方位角為90°時(shí)，套管的最大應(yīng)力隨偏心距的增大逐漸增大;當(dāng)偏心距一定，偏心方位角為90°時(shí)，套管的von Mises應(yīng)力最大.

圖3 套管偏心與最大von Mises應(yīng)力對(duì)應(yīng)關(guān)系圖Fig.3 Diagram of the casing eccentricity and the maximum von Mises stress

3 套管偏心距和偏心方位角與套管最大應(yīng)力的關(guān)系

圖4是當(dāng)ρ=15 mm時(shí)，套管最大應(yīng)力σmax隨偏心方位角φ變化的關(guān)系圖，其中橫坐標(biāo)代表偏心方位角φ，縱坐標(biāo)代表套管最大應(yīng)力σmax，“*”表示計(jì)算得到的σmax隨φ的變化關(guān)系，曲線表示用φ的二次多項(xiàng)式擬合得到的σmax值.由圖可見，可用φ的二階多項(xiàng)式近似表達(dá)σmax.設(shè)

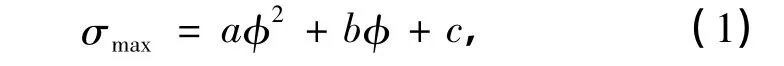
式中，a，b，c為擬合系數(shù).當(dāng)ρ=15 mm時(shí)，可得擬合系數(shù)為a=－0.001 8，b=0.317 7，c=752.669 8.

圖4 ρ=15 mm時(shí)偏心方位角擬合曲線Fig.4 Fitted curve of eccentricity angle when ρ=15 mm

當(dāng)偏心距ρ取不同數(shù)值時(shí)得到的對(duì)應(yīng)的擬合系數(shù)如表2所示.

表2 不同偏心距對(duì)應(yīng)的擬合系數(shù)Table 2 Fitted coefficients of different eccentricity

進(jìn)一步擬合表中a，b，c與ρ的關(guān)系，可得

將式(2)～(4)代入式(1)，可得

此模型的適用范圍為0°≤φ≤180°，0≤ρ≤20.

由式(5)可分別得出偏心距和偏心方位角對(duì)套管最大應(yīng)力的影響，如圖5和圖6所示.由圖5可知，當(dāng)偏心方位角φ=0°時(shí)，套管的最大應(yīng)力隨套管偏心距的增大而減小，隨著偏心方位角的增大，套管最大應(yīng)力隨著套管偏心距的增大而增大;當(dāng)偏心方位角φ=90°時(shí)，套管最大應(yīng)力隨偏心距增大的速率最快.由圖6可知，當(dāng)偏心距ρ=0 mm時(shí)，套管居中，隨著偏心距的增大，套管最大應(yīng)力隨套管偏心方位角變化的幅度越來越大;當(dāng)套管偏心距ρ=30 mm時(shí)，套管在不同偏心角度處的最大應(yīng)力相差近22.74 MPa.具體結(jié)果及應(yīng)力增幅如表3所示.

由表3可知，套管偏心距的增大會(huì)提高套管內(nèi)的最大應(yīng)力值.盡管最大增幅只有3.01%，但由于基數(shù)較大，使得應(yīng)力增加的最大值可達(dá)22.74 MPa，相當(dāng)于套管居中且其他條件不變，鉆井液密度降低到1.18 g/cm3時(shí)造成的應(yīng)力增量(井深4 995 m).也就是說，雖然設(shè)計(jì)的鉆井液密度值為1.25 g/cm3，但由于套管偏心，使得套管內(nèi)壁的最大應(yīng)力達(dá)到了鉆井液密度值僅為1.18 g/cm3時(shí)套管內(nèi)壁的最大應(yīng)力值.

圖5 偏心距對(duì)套管最大應(yīng)力的影響Fig.5 Effects of eccentricity on maximum stress

圖6 偏心方位角對(duì)套管最大應(yīng)力的影響Fig.6 Effects of eccentricity angle on maximum stress

表3 不同偏心距下套管內(nèi)壁最大應(yīng)力的增量與增幅Table 3 Increment of casing maximum stress on different eccentricity

因此，為了安全，采用套管居中條件設(shè)計(jì)時(shí)的最小鉆井液密度不能低于1.32 g/cm3.考慮到鉆井液密度降低對(duì)套管內(nèi)壓卸載速率的影響，可確定英買力區(qū)塊的最小鉆井液密度不應(yīng)低于1.35 g/cm3.該密度值的確定，為英買力區(qū)塊最低鉆井液密度的確定提供了很好的依據(jù)，并很好地解決了鉆進(jìn)過程中出現(xiàn)的套管變形問題.

4 結(jié)論

(1)非均勻地應(yīng)力下，套管偏心對(duì)套管最大應(yīng)力有一定的影響.套管在最大地應(yīng)力方向偏心，套管最大應(yīng)力減小，抗擠強(qiáng)度提高;套管在最小地應(yīng)力方向偏心，套管最大應(yīng)力增大，抗擠強(qiáng)度降低.實(shí)際井眼中很難保證套管的偏心發(fā)生在最大地應(yīng)力方向，所以在實(shí)際固井過程中有必要增加一定數(shù)目的扶正器，以最大限度地保證套管居中.

(2)回歸了套管偏心距和偏心方位角與套管最大應(yīng)力關(guān)系的公式.該公式能夠比較精確地計(jì)算不同偏心情況下，套管的最大應(yīng)力.計(jì)算結(jié)果與有限元法計(jì)算的最大應(yīng)力結(jié)果相比較，誤差在0.3%之內(nèi)，可滿足工程的需要.

(3)目前在實(shí)際應(yīng)用中采用本研究得出結(jié)論的最大困難是，如何求解并確定套管在井眼中的偏心特征(［ρ，φ］)，這可通過建立具有雙重非線性特征的套管柱在井眼中的受力變形模型，并通過有限元迭代方法求得.

(4)利用本方法確定了塔里木英買力區(qū)塊的最小鉆井液密度值，并取得了很好的效果.

(5)套管應(yīng)力大小與地應(yīng)力載荷密切相關(guān)，回歸公式中應(yīng)該包含地應(yīng)力參數(shù)，這部分內(nèi)容有待進(jìn)一步研究.本研究給出的回歸公式僅針對(duì)塔里木油田英買力地區(qū)特定地層應(yīng)力.

［1］ 李子豐，張永貴，楊鑫軍.蠕變地層與油井套管相互作用力學(xué)模型［J］.石油學(xué)報(bào)，2009，30(1)：129-131.

［2］ 何開平，張良萬，張正祿，等.鹽膏層蠕變粘彈性流體模型及有限元分析［J］.石油學(xué)報(bào)，2002，23(5)：102-106.

［3］ 張金成.巖鹽地層套管蠕變載荷試驗(yàn)及其數(shù)值分析［J］.中國(guó)石油大學(xué)學(xué)報(bào)：自然科學(xué)版，2009，33(1)：115-119.

［4］ 郭印同.鹽膏巖地層油氣井套管損壞機(jī)理研究［D］.武漢：中國(guó)科學(xué)院武漢巖石力學(xué)研究所，2010.

［5］ 鄧虎.熱采井中套管偏心對(duì)井筒溫度場(chǎng)和應(yīng)力場(chǎng)的影響研究［J］.石油礦場(chǎng)機(jī)械，2008，37(3)：6-9.

［6］ 丁保剛，李國(guó)慶，姜文勇，等.套管居中設(shè)計(jì)與校核［J］.石油鉆探技術(shù)，2009，37(1)：58-61.

［7］ 嚴(yán)焱誠(chéng)，薛麗娜，朱禮平，等.復(fù)合套管固井在川西水平井中的應(yīng)用［J］.天然氣工業(yè)，2009，29(2)：67-69.

［8］ 宋明，楊鳳香，宋勝利，等.固井水泥環(huán)對(duì)套管承載能力的影響規(guī)律［J］.石油鉆采工藝，2002，24(4)：7-9.

［9］ 李軍，陳勉，張輝，等.不同地應(yīng)力條件下水泥環(huán)形狀對(duì)套管應(yīng)力的影響［J］.天然氣工業(yè)，2004，24(8)：50-52.

［10］ 王小增，竇益華，楊久紅.偏心磨損套管應(yīng)力分布的雙極坐標(biāo)解答［J］.石油礦場(chǎng)機(jī)械，2006，35(3)：42-45.

［11］ 陳勇，練章華，張海清，等.考慮初始橢圓度的套管抗載荷能力分析［J］.石油礦場(chǎng)機(jī)械，2007，36(7)：35-38.