優化結構閘片對制動盤溫度及熱應力的影響

農萬華，符 蓉，韓曉明

(大連交通大學 連續擠壓教育部工程研究中心，遼寧 大連 116028)

0 引言

列車制動過程中，動能通過制動盤和閘片的摩擦轉換為熱能并被摩擦副吸收.由于制動盤在短時間內吸收大量熱量而溫度急劇上升，引起了熱應力，從而導致制動盤摩擦表面產生熱疲勞裂紋失效.制動盤的疲勞失效已引起廣泛關注，國內外學者對制動過程中制動盤的摩擦熱和熱應力進行了一些研究［1-8］.這些研究基本都集中在討論制動工況，制動加載方式，制動盤材料，制動盤結構等因素對制動盤的溫度場和應力場的影響.這些研究結果為揭示制動盤溫度分布規律做出了貢獻.然而，隨著人們對閘片產品的研究，閘片的結構形式出現多樣化，比如，構成閘片的摩擦塊布局形式多樣.那么，布局結構不同的閘片制動時，制動盤溫度及熱應力的大小和分布均有差異.因此對閘片結構的研究，對于分析制動盤的溫度和熱應力的分布就顯得尤為重要了，目前國內鮮有關于閘片摩擦塊布局結構是如何影響摩擦副的摩擦熱量分布及制動盤溫度場和應力場的報道.本文從閘片結構的角度，提出了一種優化閘片摩擦塊的固定位置的方法，利用有限元軟件ABAQUS，對制動盤溫度場和應力場進行數值仿真研究，為閘片的設計提供理論依據.

1 閘片優化

1.1 結構因子的提出

制動過程通過閘片與制動盤的摩擦，摩擦力所做的功轉變成熱能被制動盤吸收.故施加在制動盤每側摩擦面區域的熱流密度為

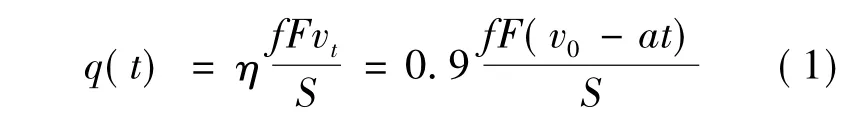
式中，q(t)為制動盤摩擦面等效熱流密度;η為摩擦功轉換為熱能的效率;f為制動盤和閘片之間的摩擦系數;F為閘片對制動盤的正壓力;v0為列車制動初速度;a為制動減速度;t為制動時間;S為閘片的摩擦面積.

取摩擦面上一點為研究對象，由式(1)得則該點的瞬時熱流密度為

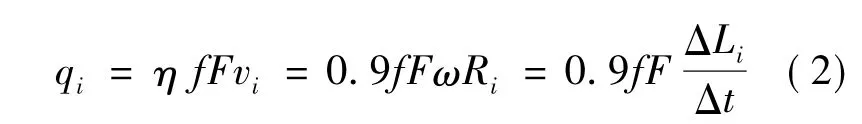
式中，qi為制動盤摩擦面上某點瞬時熱流密度;η為摩擦功轉換為熱能的效率;f為制動盤和閘片之間的摩擦系數;F為閘片對制動盤的正壓力;vi為該點處的線速度;ω為制動盤的角速度;Ri為摩擦半徑;ΔLi為制動單位時間Δt內該點實際滑動距離.

由式(2)可知，當制動壓力一定時，在盤半徑為R的圓周上的瞬時總熱流密度與該處摩擦副接觸的弧長有關，摩擦副接觸弧長越大該處的總熱流密度也越大，即盤半徑為R的圓周上的總熱流密度正比于該處摩擦副接觸弧長：

式中，q'為在盤半徑為R的圓周上的瞬時總熱流密度;L為閘片在盤半徑為R的圓周上接觸摩擦的弧長之和.

為了從能量分配的角度，表征閘片結構的特征，提出結構因子N的定義如下：

式中，N為結構因子;R為摩擦半徑;L為摩擦副在盤半徑為R的圓周上接觸弧長之和;R0制動盤的外圓半徑.

實際上，結構因子N所代表的物理意義正好與盤半徑為R的圓周上的熱流密度相對應，N值越大輸入的熱流密度也就越大.結構因子N的變化規律反映了能量在制動盤徑向的分布規律，也就是說結構因子N既可體現摩擦熱能分配狀態，也可表征閘片結構的差異.

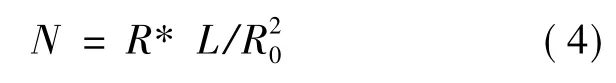
1.2 閘片結構優化計算

通過以上分析可知，結構因子與摩擦過程中能量的分布存在一定的關系，而制動盤的溫度場和熱應力場又受到輸入能量的影響.所以對結構因子的優化，便可改善制動盤的溫度場和熱應力場.

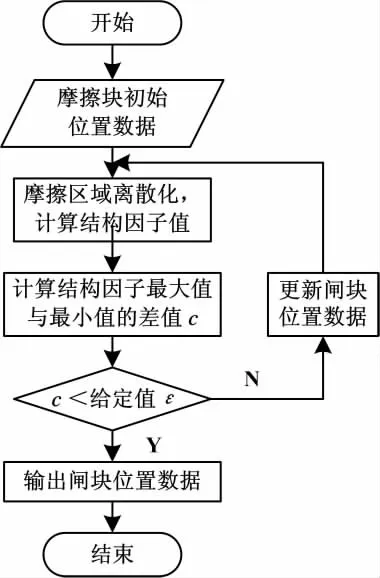
圖1 摩擦塊布局優化計算流程圖

閘片優化計算流程圖1所示.首先給出閘片摩擦塊的任意位置，然后對摩擦副的摩擦區域離散，計算出結構因子，找出其中的最大值和最小值，做差得差值c，通過調整制動塊在徑向的排布，使得差值c小于給定值ε，通過以上方法找到結構因子波動范圍最小的閘片結構.

2 制動盤溫度場和應力的數值模擬

2.1 摩擦副數值模擬模型

本文以9個圓柱摩擦塊組成的閘片為例，采用數值模擬的方法，對經過結構優化和未優化的閘片制動時，制動盤的溫度及熱應力進行了計算.圖2為結構優化前后的閘片模型，圖3為優化前后的結構因子變化曲線.由圖可見，隨摩擦半徑增大，閘片P1的結構因子增大，閘片P0的結構因子基本保持水平，波動范圍在0.34之間，大概占結構因子數值的15%，可見，閘片P0的結構因子在徑向的波動已明顯減小.

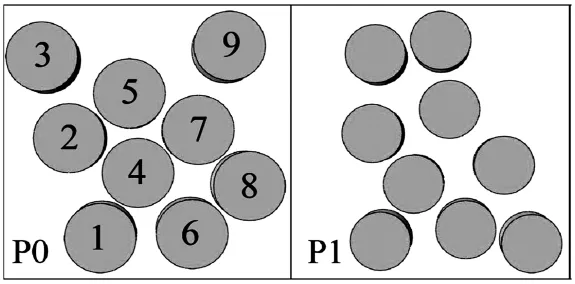
圖2 結構優化后閘片P0和未化閘片P1模型

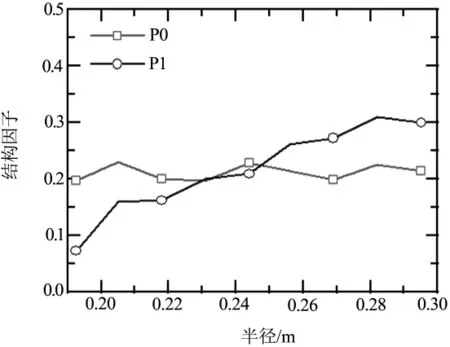
圖3 結構因子與摩擦半徑關系

制動盤與制動塊相關幾何參數見表1.制動盤材料是鍛鋼，閘片材料是銅基粉末冶金材料，材料的性能參數見表2.

表1 制動盤與摩擦塊幾何參數

表2 摩擦副材料性能參數

模擬的制動初始速度為200 km·h-1，制動時間為10.9 s，制動過程假定為勻減速運動，其減速度為1.27 m·s-2，制動末速度為150 km·h-1.環境溫度和摩擦副的初始溫度均設為20℃.設定制動壓力p=0.5 MPa，制動盤與閘片間的摩擦系數設定為 μ=0.35.

2.2 數值模擬結果對比分析

圖4是在制動時間達10.9 s時，制動盤表面溫度分布情況.可見，從溫度分布的均勻性看，制動盤P0的溫度分布已基本均勻，制動盤P1的盤面溫度呈高低相間分布.制動盤P0的最高溫度出現在盤半徑較小區域，制動盤P1的最高溫度出現在盤半徑較大區域.制動盤P0的盤面溫度明顯下降.

圖4 制動盤表面溫度分布云圖

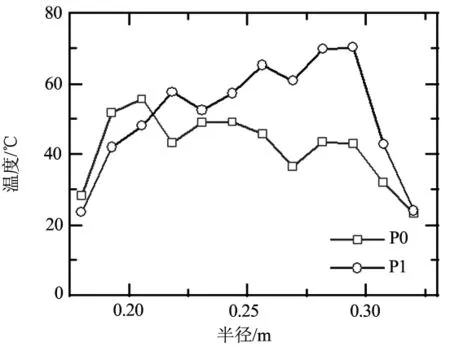
圖5 盤面溫度隨盤半徑變化曲線

圖5是在制動時間達10.9 s時，制動盤表面的節點溫度與盤半徑的關系曲線.可見，制動盤P0的溫度明顯低于制動盤P1，制動盤P0的盤面最高溫度為55℃，制動盤P1的盤面最高溫度為70℃.經優化后，盤面最高溫度下降15℃，下降幅度占優化前的21%.隨盤半徑增加，制動盤P1的盤面節點溫度逐漸升高，制動盤P0的盤面節點溫度逐漸下降.制動盤P1摩擦區域的溫度波動范圍為30℃，而制動盤P0摩擦區域的溫度波動范圍為25℃，下降幅度為17%.由此可見，制動盤P0與制動盤P1相比，盤面最高溫度顯著下降，摩擦區域溫度波動范圍明顯減小，優化效果顯著.

圖6是在制動時間達10.9 s時，制動盤表面熱應力分布情況.可見，制動盤P0的最大熱應力出現在盤半徑較小區域，制動盤P1的最大熱應力出現在盤半徑較大區域.制動盤P0的熱應力明顯下降.

圖6 制動盤表面熱應力分布云圖

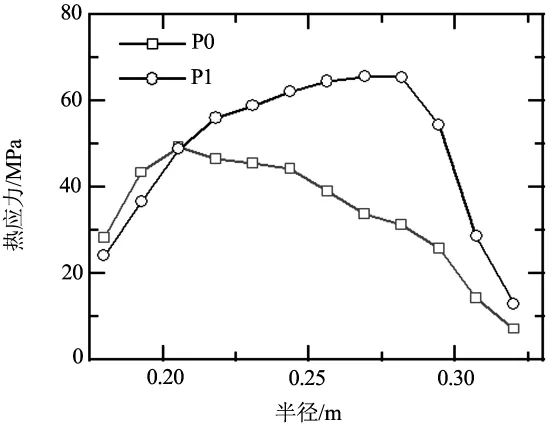
圖7 盤面熱應力隨盤半徑變化曲線

圖7是在制動時間達10.9 s時，制動盤表面熱應力與盤半徑關系曲線.可見，隨摩擦半徑增大，制動盤P1的熱應力逐漸升高，制動盤P0的熱應力逐漸下降.制動盤P1的盤面最大熱應力出現在盤半徑為290 mm處，數值為65 MPa，制動盤P0的盤面最大熱應力出現在盤半徑為205 mm處，數值為50 MPa.優化后制動盤最大熱應力下降15 MPa，下降幅度占優化前最大熱應力的23%.這說明經過優化后，制動盤表面最大熱應力顯著下降.

3 結論

分析了制動盤上一點能量輸入與閘片結構之間的關系，認為閘片結構的差異直接影響到制動盤能量的輸入，提出了影響制動盤摩擦表面溫度場和應力場分布的閘片結構因子的概念，和一種對閘片結構因子優化方法，利用該方法對閘片結構進行了優化.

利用有限元軟件ABAQUS對優化前后的閘片進行制動過程的數值模擬，結果表明閘片結構優化后，制動盤的溫度場和應力場的最大值較閘片未優化時有所下降，沿制動盤徑向分布的波動程度較未優化時小.

［1］莊光山，王成國，王海慶，等.盤形制動摩擦表面溫升研究［J］.機械工程學報，2003，39(2)：150-154.

［2］丁群，謝基龍.基于三維模型的制動盤溫度場和應力場計算［J］.鐵道學報，2002，21(6)：35-38.

［3］楊鶯，王剛.機車制動盤三維瞬態溫度場與應力場仿真［J］.機械科學與技術，2005，24(10)：1257-1260.

［4］趙文清.高速列車“中華之星”制動盤溫度場及熱應力［J］.兵工學報，2006，27(1)：132-136.

［5］劉金朝，卜華娜，劉敬輝，等.整體制動盤熱應力有限元仿真分析［J］.中國鐵道科學，2007，28(2)：80-83.

［6］趙海燕，張海全，湯曉華，等.快速列車盤型制動熱過程有限元分析［J］.清華大學學報，2005，45(5)：589-592.

［7］陳德玲，張建武，周平.高速輪軌列車制動盤熱應力有限元研究［J］.鐵道學報，2006，28(2)：39-43.

［8］王文靜，謝基隆，劉志明，等.基于循環對稱結構制動盤的三維瞬態溫度場仿真［J］.機械工程學報，2002，38(12)：131-134.