一般非線性離散系統P-D 型迭代學習收斂性研究
劉長良,賈萬根
0 引言
迭代學習控制 (Iterative Learning Control,ILC)作為學習控制的一個重要研究方向,是智能系統中具有嚴格數學描述的一個分支。自Arimoto開創性的提出迭代學習控制概念以來,研究人員針對不同類型的對象[1~6],提出了形式多樣的迭代學習控制律[7~11],并在一定的前提假設條件下,利用微積分不等式、Lyapunov 理論、λ 范數、2 -D 理論等各種數學工具,分析得到了收斂性的條件。雖然迭代學習控制一直是控制界的研究熱點領域之一,但大多只是針對一類特定的系統。對于一般的非線性系統,由于結構、參數等很不確定而且非線性環節的存在使得系統控制器的研究變得復雜,所以針對一般的非線性系統的研究成果相對較少。文獻[12]給出了一般非線性離散系統開環PID 的迭代學習控制收斂性的充分條件及實現條件,并做了嚴格的數學證明。然而,理論研究表明[13]:閉環迭代律的控制性能比開環控制性能要好,收斂速度也較快。因此,文獻[14]在文獻[12]的基礎上應用范數和歸納法理論,證明了一般非線性離散系統閉環P 型迭代學習控制的收斂性。為了同時利用系統當前運行和前次運行的信息,以便進一步改善控制性能,本文針對一般的非線性離散系統給出了P-D 型開閉環迭代學習控制收斂性的充分條件。
1 問題描述
考慮一般的非線性離散系統
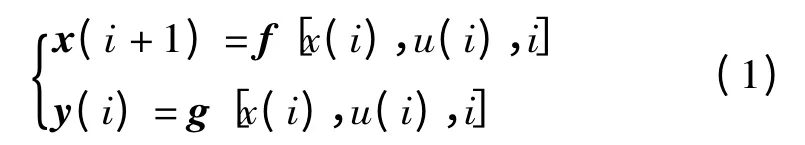
其中,
x(i)∈Rn×1;u(i)∈Rm×1;y∈Rr×1;f,g 為矩陣函數。系統結構和參數未知。所要解決的問題是:要求系統在給定的時間區間[0,N ]上跟蹤期望輸出yd(i)。假設期望控制ud(i)存在,即:在給定狀態初值x (0)下ud(i)是上述方程組的解,則迭代控制的目的是通過多次重復的運動,在一定的學習律下使
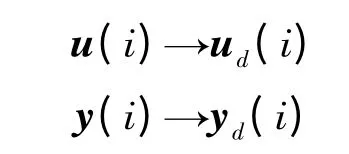
第k 次運行時離散系統表達式為
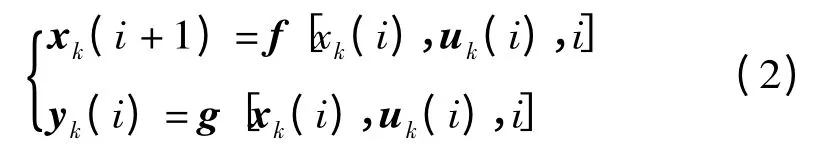
輸出誤差為

2 非線性離散的P-D 型開閉環迭代學習收斂性
取開閉環P-D 型控制律,即其開環采用D 型ILC,閉環采用P 型ILC。
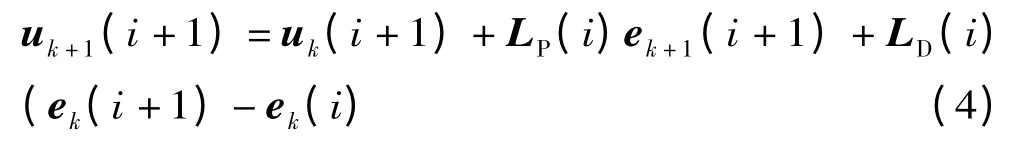
式中:k 為迭代次數;LP(i)為閉環迭代系數;LD(i)為開環迭代系數。
定義1 定義誤差函數的λ 范數為

其中,0 <λ <1。
定理1 如果系統(1)滿足條件:
(1)f,g 是連續的函數矩陣。
(2)f,g 關于x,u 的偏導數存在,且滿足Lipschitz 條件。記f,g 在第k 次迭代時關于x,u的偏導數分別為fxk,fuk,gxk,guk。
(3)每次學習時的初始狀態、初始控制量都相同xk(0)=x0,uk(0)=u0。
(4)矩陣(I + gukLP(i))-1存在 (I 為單位陣)。則非線性離散系統 (1)采用學習律 (4)進行迭代學習控制,輸出y (i)以任意精度跟蹤期望輸出yd(i)的充分條件為
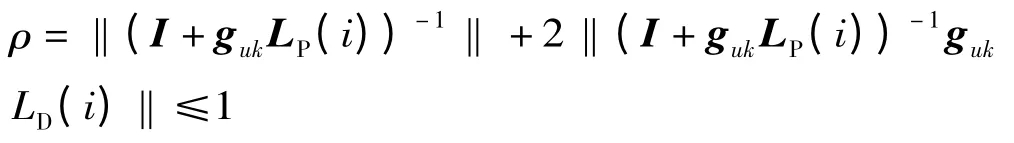
證明:取第k+1 次迭代時的誤差函數
將開閉環P-D 型迭代學習控制律(4)代入上式得
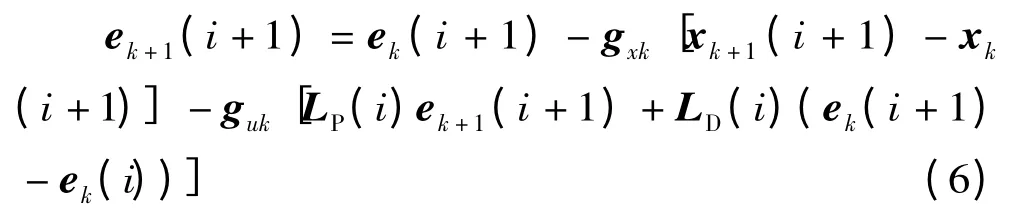
即
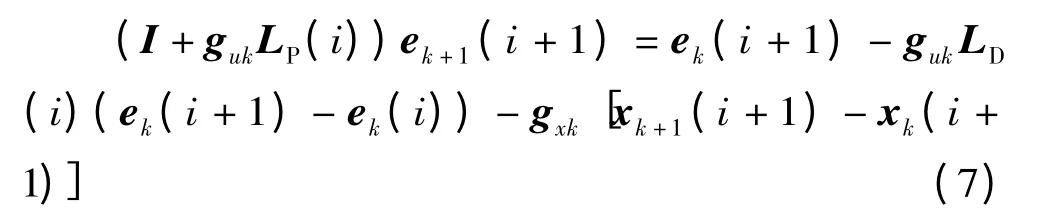
由條件(4)
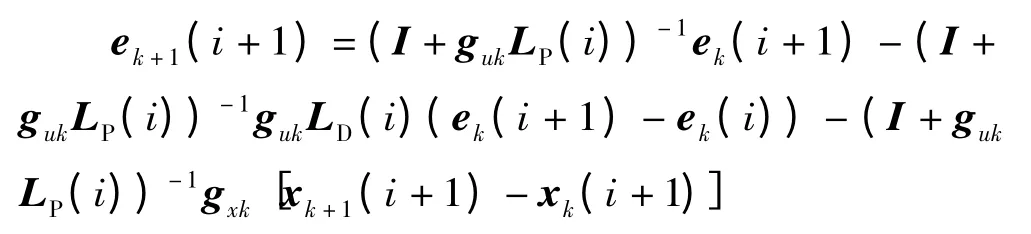
兩邊同乘λi+1,(0 <λ <1)

兩邊同取范數,有
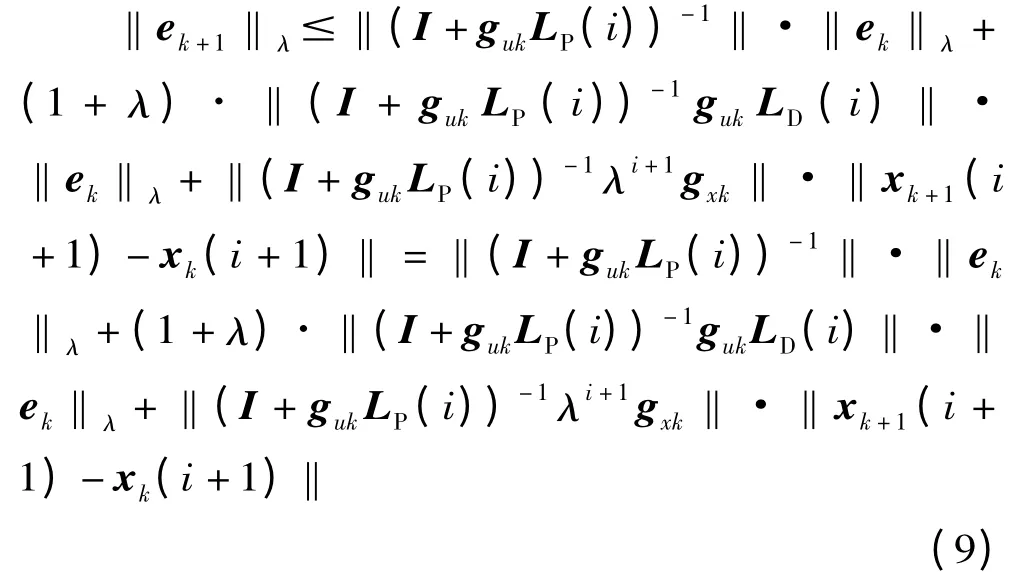
下面用數學歸納法證明:
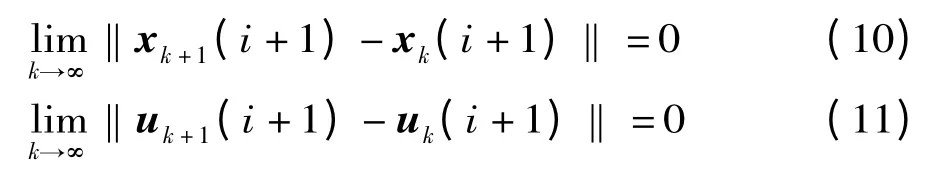
當i+1 =0 時,據定理1 中條件(3)得
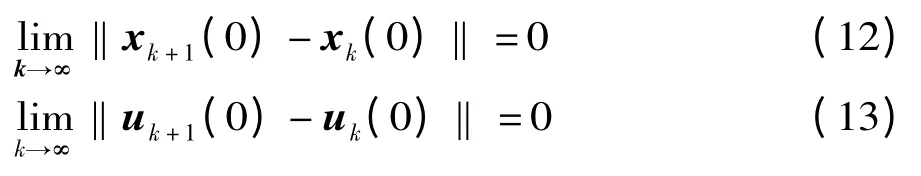
假設當i+1 =n 時,有
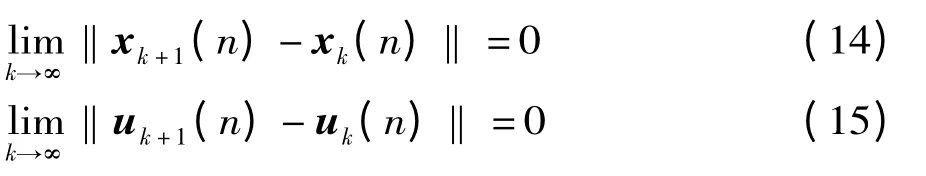
成立,則
當i+1 =n+1 時,
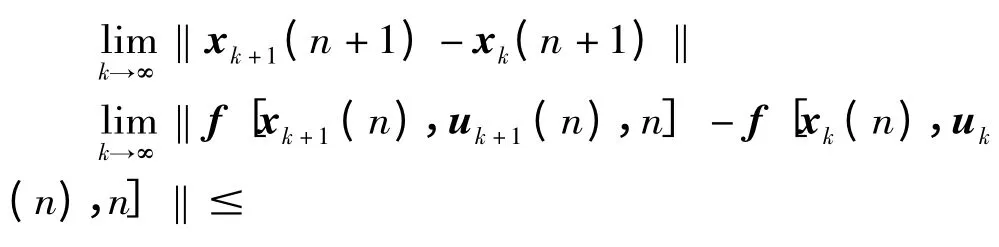
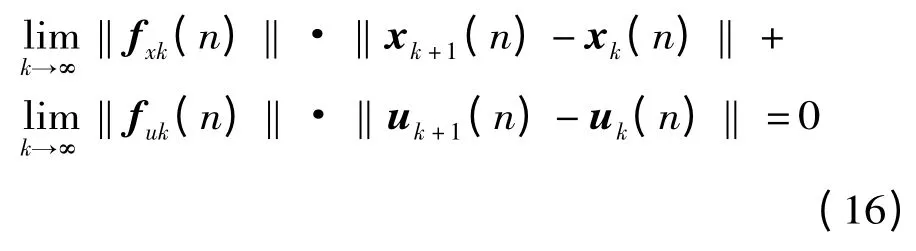
因為0 <λ <1,故
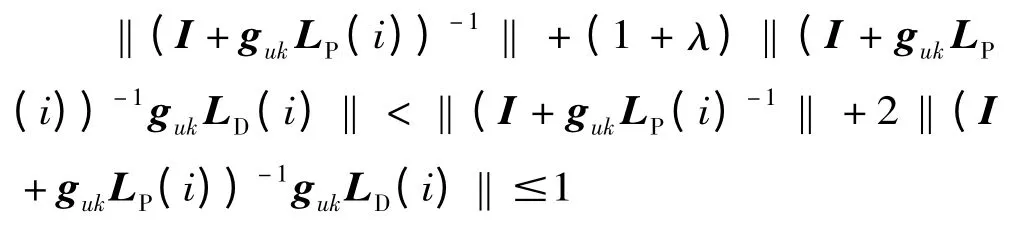
由定理1 的充分條件式(9)、式(16)及上式,有
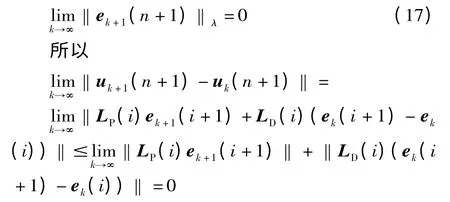
所以,式(10),(11)成立,定理得證。
3 仿真實例
根據針對一般非線性離散系統的開閉環P-D型迭代學習控制算法的收斂性證明,為了表明該算法的有效性,特此考慮如下非線性離散系統:
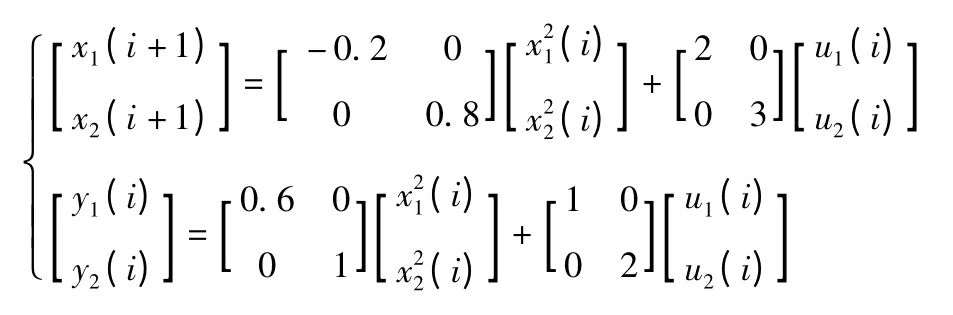
應用上述開閉環P-D 型控制律
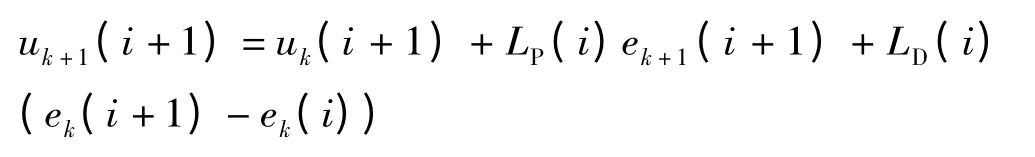
設期望輸出
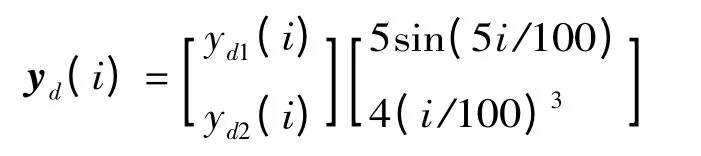
控制律(4)中LP(i),LD(i)分別取
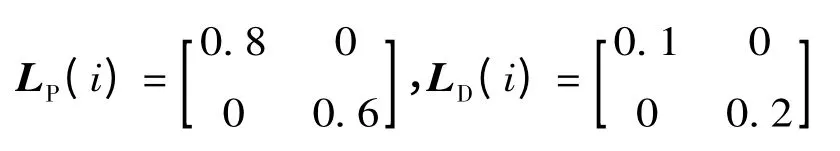
滿足條件
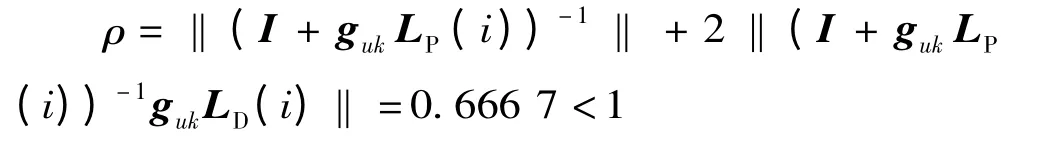
在初始狀態為零的條件下,算法(4)跟蹤期望軌跡的仿真結果如圖1 和圖2 所示。圖1 是算法(4)在第3 和第5 次時關于期望軌跡第一分量的跟蹤情況,而圖2 是算法(4)在第3 和第5次時關于期望軌跡第二分量的跟蹤情況。從圖1和圖2 可以看出,當第5 次迭代時算法(4)幾乎已經能實現完全跟蹤。從圖3 和圖4 可以很清楚地看出誤差最大值隨迭代次數的變化情況。
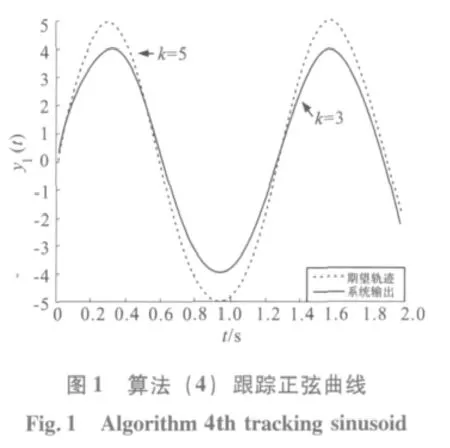
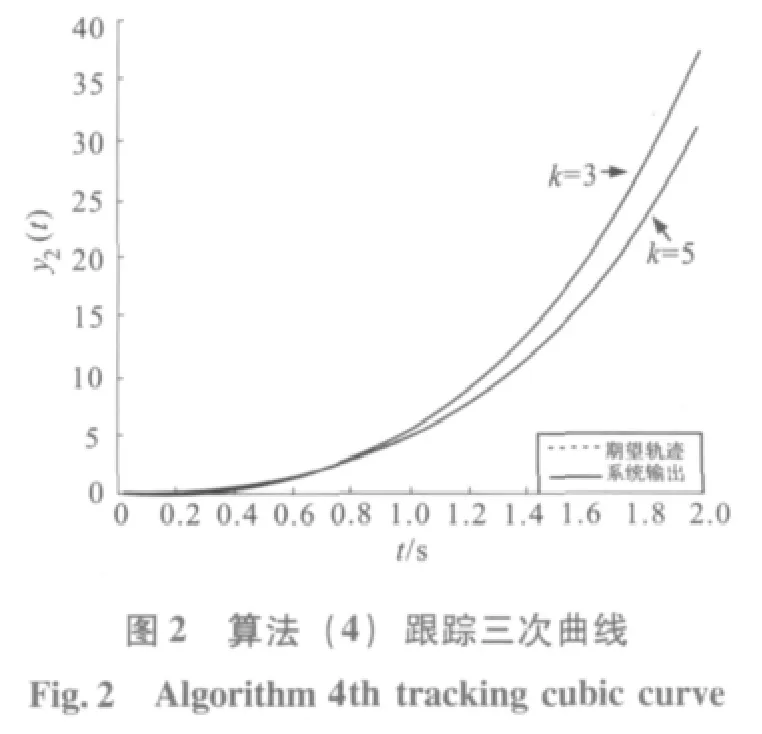
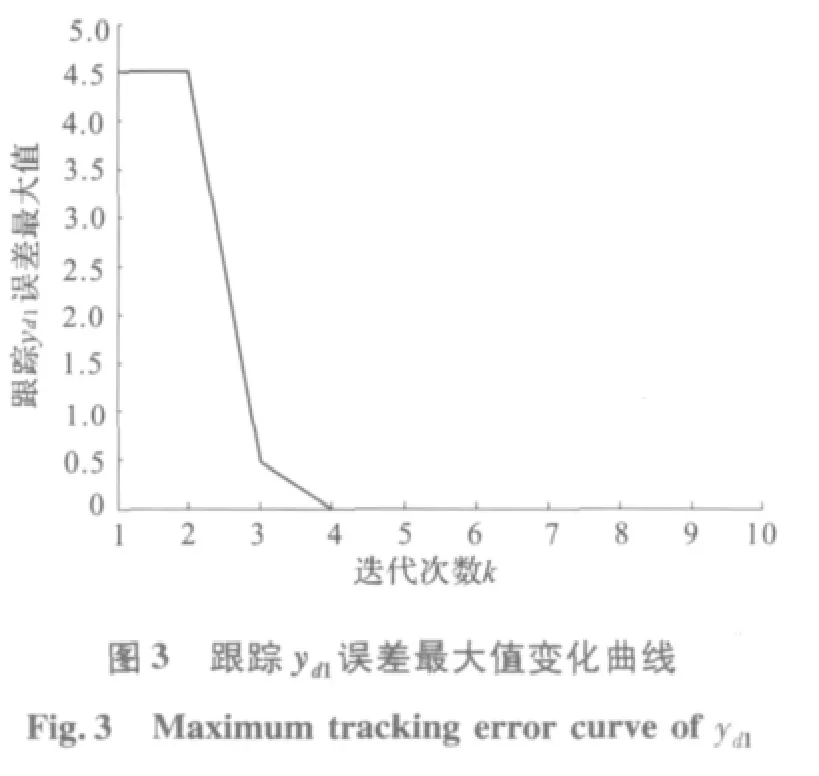

圖4 跟蹤yd2誤差最大值變化曲線Fig.4 Maximum tracking error curve of yd2
4 結論
針對一般非線性離散系統結構、參數等很不確定而且非線性環節的存在使得系統控制器的研究變得復雜的特點,在充分利用系統上次和當前運行得到的信息及閉環控制效果要優于開環的結論的條件下,本文給出了對于一般非線性離散系統的開閉環P-D 型迭代學習收斂的充分條件,仿真結果表明了該充分條件的正確性。
[1]謝振東,劉永清.分布參數系統目標跟蹤的二階P -型學習 算 法[J].暨 南 大 學 學 報,1998,19 (1):60-64.Xie Zhendong,Liu Yongqing.Two order p-type learning control algorithm of distributed parameter systems [J].Journal of Jinan University [J].1998,19 (1):60-64.
[2]田森平,謝勝利,傅予力.連續非線性系統的迭代學習控制 算 法[J].中 山 大 學 學 報,2000,39 (6):313-317.Tian Senping,Xie Shengli,Fu Yuli.Iterative learning control algorithms for nonlinear continuous systems [J].Acta Scientlarum Naturalium Universitatis Sunyatseni,2000,39(6):313-317.
[3]謝勝利,謝振東,田森平.非線性系統的迭代學習控制及其算法實現[J].控制理論與應用,2002,19 (2):167-172,177.Xie Shengli,Xie Zhendong,Tian Senping.Iterative learning control and algorithm realization of nonlinear systems[J].Control Theory & Applications,2002,19(2):167-172,177.
[4]Tayebi A,Zaremba M B.Iterative learning control for nonlinear systems described by a blended multiple model representation [J].International Journal of Control,2002,75(16):1376-1384.
[5]謝振東,謝勝利,韋崗.非線性學習控制理論及其在機器人系統上的應用[A].中國控制會議論文集[C].北京:國防大學出版社,1998.957-961.Xie Zhendong,Xie Shengli,Wei Gang.Nonlinear learning control theory and its application on the robot system [A].Paper Collection Chinese Control Conference [C].Beijing:National Defense University Press,1998.957-961.
[6]李洋,谷俊杰,支保峰,等.加權閉環PD 型迭代學習控制在重復擾動時的應用[J].電力科學與工程,2008,24 (1):48-50.Li Yang,Gu Junjie,Zhi Baofeng,et al.Application of the weighted PD-type closed-loop iterative learning control in the repeated disturbances [J].Electric Power Science and Engineering,2008,24 (1):48-50.
[7]Tian Senping,Xie Shengli.A nonlinear algorithm of iterative learning control based on vector plots analysis [C].Wuhan:Procceedings of the Second International Symposium on Intelligent and Complex Systems,2001.17-20.
[8]田森平,謝勝利,傅予力.一種新的迭代學習控制快速算法[J].華 南 理 工 大 學 學 報,2002,30 (5):37-40.Tian Senping,Xie Shengli,Fu Yuli.Fast algorithm of iterative learning control [J].Journal of South China University of Technology,2002,30 (5):37-40.
[9]Qu Z.An iterative learning algorithm for boundary control of a stretched moving string [J].Automatica,2002,38(5):821-827.
[10]Xie Shengli,Tian Senping.A fast algorithm of iterative learning control based on the geometric analysis[C].Xiamen:Proceedings of the 2002 International Conference on Control Theory and Automation,2002. 472-476.
[11]謝勝利,田森平,謝振東.基于幾何分析的迭代學習控制快速算法[J].控制理論與應用,2003,20 (3):419-422.Xie Shengli,Tian Senping,Xie Zhendong.Fast algorithm of iterative learning control based on geometric analysis[J].Control Theory & Applications,2003,20 (3):419-422.
[12]史忠科.非線性離散系統的迭代學習控制方法及其應用[J].控制理論與應用,1998,15 (3):327-332 Shi Zhongke.Iterative learning control method for nonlinear discrete-time systems [J].Control Theory & Applications,1998,15 (3):327-332.
[13]曾南,應行仁.非線性系統迭代學習算法[J].自動化學報,1992,18 (2):168-176.Zeng Nan,Ying Xingren.Iterative learning control algorithm for linear dynamical system [J].Acta Automatica Sinica,1992,18 (2):168-176.
[14]高衛華,謝劍英.一般非線性離散系統的閉環迭代學習控制研究[J].系統仿真學報,2001,13 (1):73-74,109.Gao Weihua,Xie Jianying.Closed-loop iterative learning control for general nonlinear discrete system [J].Journal of System Simulation,2001,13 (1):73-74,109.

