杠桿法在復合輪系教學上的應用

李明圣

（湛江師范學院物理科學與技術學院，廣東 湛江 524048）

在機械中，常用到由幾個基本周轉輪系或定軸輪系和周轉輪系組合而成的復合輪系。由于整個復合輪系不可能轉化成一個定軸輪系，所以不能只用一個公式來求解。計算復合輪系時，首先必須將各個基本周轉輪系和定軸輪系區分開來，然后分別列出方程式，最后聯立解出所要求的傳動比[1]。但是對初學者來說，不易區分周轉輪系和定軸輪系，計算傳動比過程也比較繁瑣。因此，本文從行星齒輪機構的運動特性方程式出發，介紹了一種對行星齒輪機構進行運動學和動力學分析的圖解方法-杠桿法，并應用杠桿法對汽車自動變速器中的典型行星齒輪機構進行傳動比的分析。

1 行星齒輪機構傳動的一般規律

單級行星齒輪系的傳動比計算可通過轉換將周轉輪系轉換成定軸輪系，然后按求解定軸輪系傳動比的方法來計算，如公式（1）。并可得出單級行星齒輪系的傳動比通用計算公式

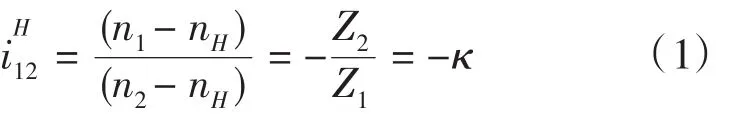
根據能量守恒定律，三個元件（太陽輪、齒圈、行星架）上輸入和輸出的功率的代數和應等于零。得出單級行星齒輪機構一般運動規律的特性方程式[2]：

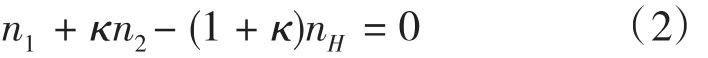
其中：n1、n2、nH、κ1分別為太陽輪轉速、齒圈轉速、行星架轉速和齒圈與太陽輪的齒數比。

由于雙級行星齒輪機構多一對行星輪外嚙合，因此公式（1）的負號變正號，傳動比的計算公式

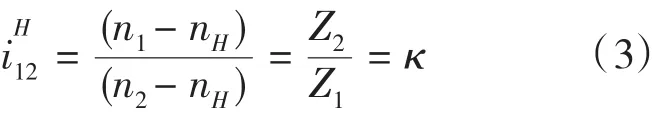
雙級行星齒輪機構一般運動規律的特性方程式：

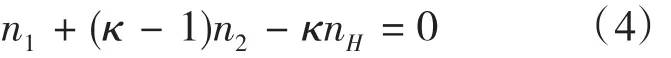
有級變速的自動變速器采用的行星齒輪傳動是一種常嚙合傳動，其傳動比變換可通過分離與接合離合器或制動器而方便的實現，而且通過增減行星排內行星齒輪的數目、行星排的數目，改變排與排之間的排列組合以及構件間的連接和控制方式，可以得到較為理想的傳動比。傳動比計算方法通常采用解方程法，即根據式（2）或式（4）列出各行星排三元一次聯立方程，確定方程中各轉速的關系，輸入、輸出元件以及各排中的共體元件。具體為：先解出轉速為0的(有制動)單排方程，解出以共體元件為主函數的方程；再以此方程代入另一方程中的共體元件，就可將雙聯方程變為只有輸入、輸出轉速的單列方程；將輸入轉速放在等號左邊，輸出轉速放在等號右邊，解出輸入軸轉速和輸出軸轉速關系的方程，再除去轉速，即得到輸入軸與輸出軸的速比。這種算法對單排和雙排行星齒輪傳動分析還比較簡單，但分析多排行星齒輪傳動時就比較困難了，特別是在判斷機構可能實現的傳動比數目、各基本構件、行星輪的相對轉速及力學和動力學問題時，非常困難。如果采用杠桿法進行分析，上述問題就變得容易，學生理解起來很輕松。

2 杠桿法的工作原理

2.1 單行星排齒輪傳動時杠桿圖

由于一個行星排由太陽輪、行星輪、齒圈及行星架構成。根據其結構特點將一個行星排等效為一個垂直杠桿和三個支點，三個支點分別代表太陽輪S、行星架PC和齒圈R。對于單行星行星排，由公式（3）和能量守恒定理可得出中間支點為行星架PC，兩端支點分別為S和R；對于雙行星行星排，由公式（5）和能量守恒定理可得出中間支點為齒圈R，兩端支點分別為PC和S。支點S和R距支點PC的長度分別與太陽輪齒數和齒圈齒數成反比，如圖1（a）、（b）所示為單行星行星排和雙行星行星排的杠桿圖，圖中為齒圈與太陽輪的齒數比。可以用杠桿圖進行行星齒輪的轉速分析，建立xoy坐標系，三個支點按比例畫在y軸，x軸表示支點的轉速大小和方向，在這里假設輸入支點的轉速為1，方向朝x軸方向為正，相反為負，被固定支點的轉速為 0。如圖 2（a）、（b）所示，圖(a)為單行星行星排轉速分析圖，齒圈R輸入、太陽輪S被固定，行星架PC輸出，利用相似三角形定理，行星架的轉速nPC=κnR/（κ+1），屬于減速同向，與公式（3）計算結果一樣；圖(b)為雙行星行星排轉速分析圖，行星架PC輸入、太陽輪S被固定，齒圈R輸出，利用相似三角形定理，齒圈的轉速nR=（κ-1）nPC/κ，屬于減速同向，與公式（5）計算結果一樣，但杠桿法更簡單、直觀。

圖1 星排杠桿圖

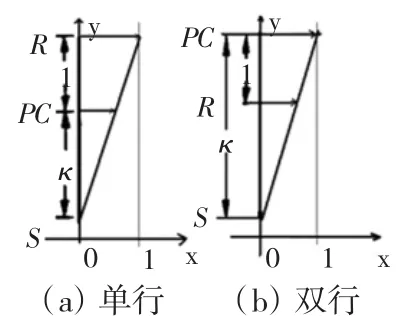
圖2 星排轉速圖

2.2 多行星排行星齒輪傳動時杠桿圖

當多行星排并聯時，每個行星排視為一個垂直的杠桿和三個支點，行星排之間的構件相互連接，在杠桿圖上視為各支點之間的連接。在處理時，根據需要，既可以將杠桿重疊，又可以將杠桿分開：重疊時，將相互連接的部分合并為一個點；將杠桿分開時，連接點用一水平線來表示。兩種情況都要對杠桿的力臂進行調整，調整時要保證連接部分合并點之間的力臂長度相等，并且各杠桿力臂長度比不變，這樣將多個行星排的杠桿圖合并為一個總杠桿圖，并在圖上標上離合器C、制動器B、單向離合器F以及輸入構件i，輸出構件o，即得多行星排并聯機構的轉速杠桿圖[3]。如圖3所示為辛普森式行星齒輪機構轉速圖，其中，（a）圖為行星齒輪機構的示意圖；（b）圖為行星齒輪機構轉速圖，C2B2（或F）接合得到1檔，連C2B2與PC1R2相交，交線段長度為輸出轉速的大小，方向與輸入同向。同樣方法，C2B1接合得到2檔，C2C1接合得到3檔，C1B2接合得到R檔。

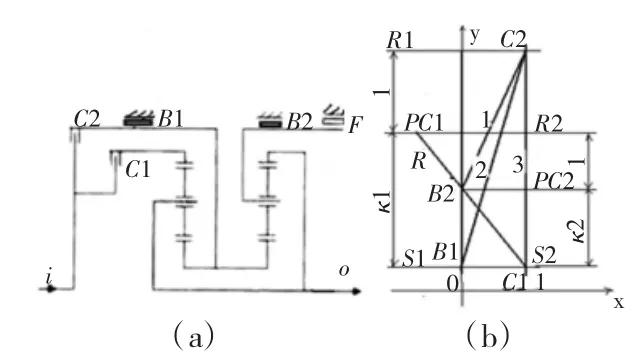
圖3 辛普森式行星齒輪機構轉速圖

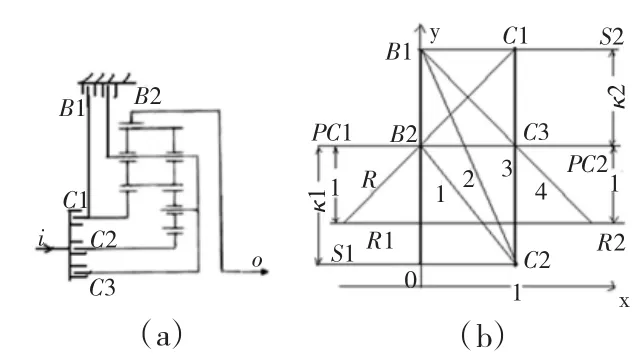
圖4 拉威娜式行星齒輪機構轉速圖

如圖4所示為拉威娜式行星齒輪機構轉速圖。其中，（a）圖為拉威娜式行星齒輪機構結構的示意圖；（b）圖為拉威娜式行星齒輪機構轉速圖，C2B2接合得到1檔，連C2B2與R相交，交線段長度為輸出轉速的大小，方向與輸入同向。同樣方法，C2B1接合得到2檔，C2C3接合得到3檔，C3B1接合得到4檔，C1B2接合得到R檔。各檔位傳動比的大小可通過相似三角形的方法求解。

2.3 各檔位下傳動比

參見圖 3（b）、圖 4（b），假設輸入件構件的轉速為1，制動件構件轉速為0，輸出構件轉速為該檔位的轉速線的長度，方向與x軸向同為正，相反為負，利用相似三角形的關系，很快可以得出此時的傳動比。辛普森式自動變速器和拉威娜式自動變速器各檔傳動比的大小，如表1和表2所列。

表1 辛普森式自動變速器各檔傳動比

表2 拉威娜式自動變速器各檔傳動比

3 杠桿法的具體應用

現以ZF公司生產的5速電子控制自動變速器5HP-24為例，應用杠桿法來分析它的傳動路線及傳動比。

5HP-24自動變速器動力傳遞路線示意圖如圖5（a）所示。由圖可知，行星齒輪組由三個單級行星齒輪機構組成。行星排1的行星架與行星排2的內齒圈相連；行星排1的內齒圈與行星排2的行星架及行星排3的內齒圈相連；行星排2和行星排3的太陽輪相連。行星排3的行星架是動力輸出端。變速器內部共有7個換擋執行元件，包括3個離合器、3個制動器和1個單向離合器。

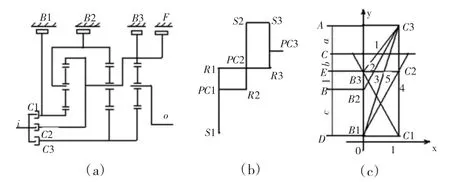
圖5 5HP-24自動變速器杠桿圖

3.1 建立5HP-24傳動機構的杠桿圖

在三行星排并聯時，每個行星排視為一個垂直的杠桿和三個支點，行星排之間的構件相互連接，在杠桿圖上視為各支點之間的連接。三行星排并聯時，在杠桿圖上有五個個支點，如圖5（b）所示，各支點的距離由行星輪的特性系數κ決定。

3.2 計算5HP-24傳動機構各檔位下傳動比

合并圖 5（b）的杠桿圖，建立圖 5（c）所示的杠桿轉速圖。假設輸入件構件的轉速為1，制動件構件轉速為0，輸出構件轉速為該檔位的轉速線的長度，方向與x軸向同為正，相反為負，利用相似三角形的關系，求各檔的傳動比。設 AC= α、CE=b、ED=1、DB=c，其中，各檔的傳動比見表3。從轉速圖可知，三行星排這種并聯布置形式可實現六個前進檔，但這款變速器只采用前五檔。

表3 5HP-24自動變速器各檔傳動比

4 結束語

（1）在教學中，首先讓學生掌握杠桿法的工作原理，單行星齒輪排轉速分析圖的畫法，這點很重要，是應用杠桿法的關鍵。

（2）畫多行星排行星齒輪傳動時杠桿圖時，相互連接的部分重疊時合并為一個點，將杠桿分開時，連接點用一水平線來表示；保證連接部分合并點之間的力臂長度相等，并且各杠桿力臂長度比不變。

（3）杠桿法不但可以計算并聯行星齒輪排的傳動比，各構件的相對轉速也可通過杠桿法轉速圖進行分析。

[1]楊可禎，程光蘊，李仲生.機械設計基礎[M].北京：高等教育出版社，2006．

[2]陳家瑞，馬天飛.汽車構造[M].北京：人民交通出版社，2006.

[3]李興華，何國旗，等.效杠桿法分析行星齒輪傳動[J].機械傳動，2004，(1):44-45．