統一強度理論下樁基極限承載力討論
謝新斌 馮小平 周顯川
1新疆地礦局第十地質大隊(848000) 2新疆地礦局第十地質大隊(848000)
0 引言
朗肯,太沙基,邁耶霍夫[1]等經典地基極限承載力公式是基于Mohr-Coulomb準則推導。但Mohr-Coulomb準則未考慮中間主應力的影響。由Mohr-Coulomb強度準則推導的地基極限承載力并不能完全反映地基實際情況,推導結果偏于保守,不能充分發揮土體的強度潛能。周小平[2~4]基于統一強度理論的太沙基地基極限承載力,利用統一強度理論求解條形地基極限承載力和考慮中間主應力的太沙基地基極限承載力公式均表明當考慮中間主應力影響時地基極限承載力會提高。
1 統一強度理論
統一強度理論可以表示為[5]:


2 基本假設
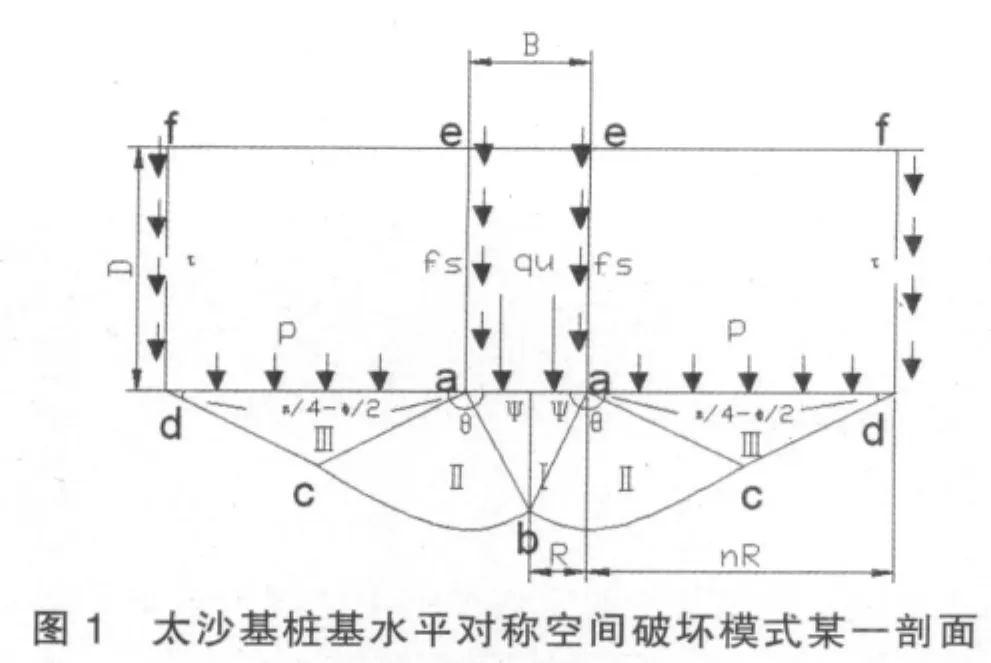
1)當地基發生整體剪切破壞,發生如圖1所示的太沙基深基礎破壞模式[6]。基底平面以下形成連續的滑動面,如取一剖面描述則其滑動面一直延伸到基底面并交于d點,滑動面由直線ab、對數螺旋曲線bc和直線cd三部分組成。
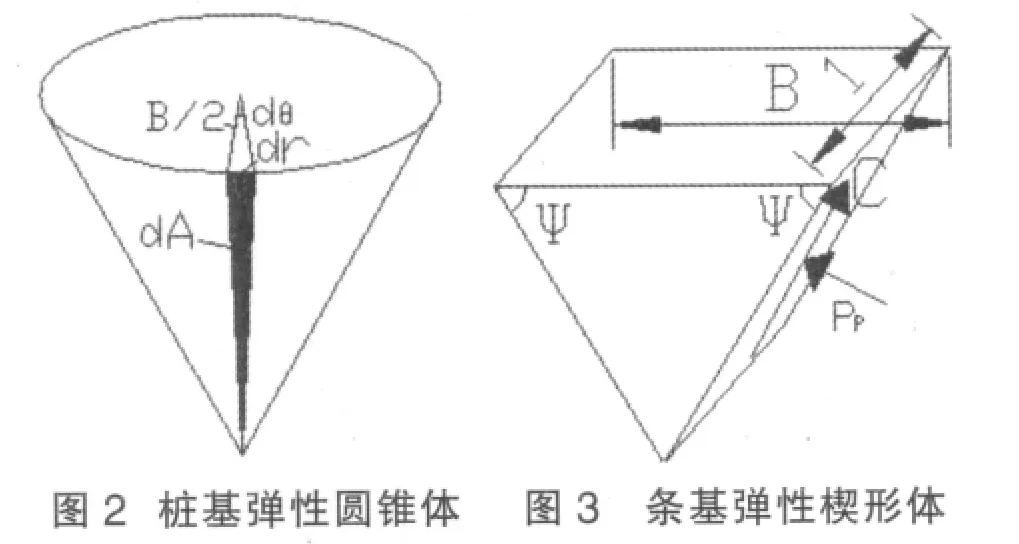
2)基底以下有一部分土體將隨基礎一起移動而始終處于彈性狀態,該部分土體為彈性圓錐體。彈性圓錐體的母線ab為滑動邊界的一部分,ab線與水平面成ψ角,并且假設作用在彈性圓錐體側面上的被動土壓力和粘聚力在母線方向的合力為作用在圓錐體側面的的圓形分布的線荷載。
3)除彈性圓錐體外,在滑動區域范圍內的所有土體處于塑性狀態,滑動區由徑向剪切區Ⅱ和朗肯被動區Ⅲ組成,徑向剪切區的邊界bc由對數螺旋曲線表示:

式中:φuni為統一強度理論的內摩擦角,r0為起始矢徑,θ為任意矢徑與起始矢徑r0的夾角。朗肯被動區Ⅲ的邊界cd為直線與水平面成45°-φuni/2角。
4)基底平面ad環形區域下的土直接受到基礎下的土所給予的側向擠壓,使這塊土有向上移動并驅使環形面積ad以上的土體也產生了向上的相對移動,從而在環形面積以上土體的邊界de和基墩側面與土之間分別產生了向下的剪阻力τ和摩阻力fs。
3 樁基極限承載力的確定
首先計算基底以上ad環形區域的受力狀態,基礎側面上的法向應力σα按靜止壓力分布,若樁基礎側面與土之間的摩擦角為δ,則作用于基礎側面上的平均法向應力σα和τα為:
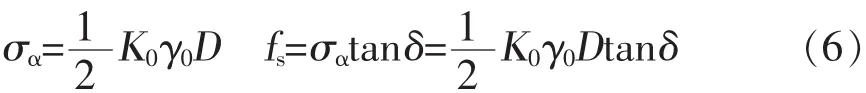
式中:K0為土的靜止側壓力系數,γ0為基礎底面以上土的容重,D為樁基的埋置深度。
環形區域的外環破壞面土的平均剪阻力假定為:

根據上述基本假定由圖2中的圓錐形彈性體的平衡條件可得整體剪切破壞時的極限荷載。

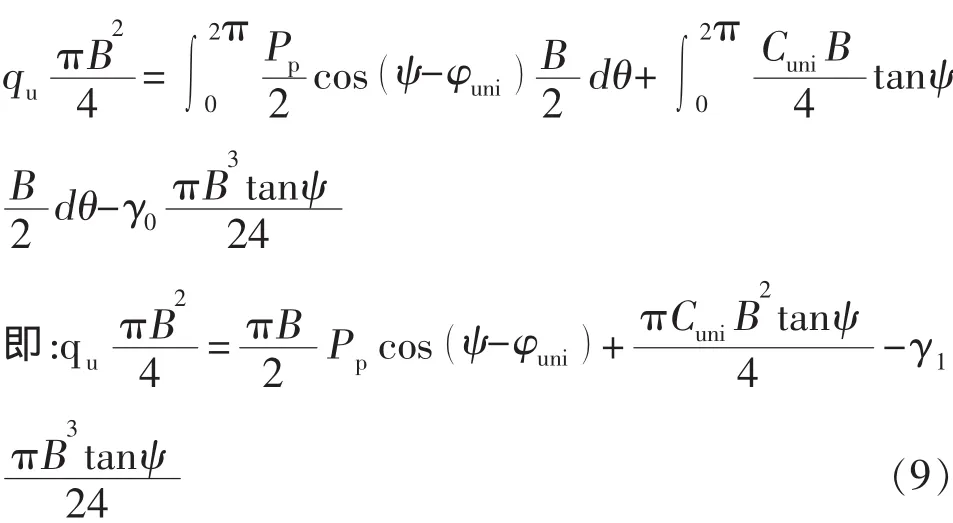



若基礎完全粗糙,此時彈性圓錐體ab與基底水平面的夾角,則式(17)可以寫成如下形式:


將式(16)代入式(13),則基底完全光滑的承載力系數 Nc,Nq,Nγ可確定。
4 計算算例及結論對比分析
有一直徑400mm的圓形樁基礎,打入均質黏性土6m,黏性土容重為20 kN/m3,固結不排水抗剪強度指標C0=20 kPa,φ0=30°。設土的靜止側壓力系數0.45,樁基與土之間的內摩擦角為δ=12°。下邊分別利用文中公式和太沙基公式求樁基極限承載力并加以比較(僅計算)。
基底完全粗糙的情況:

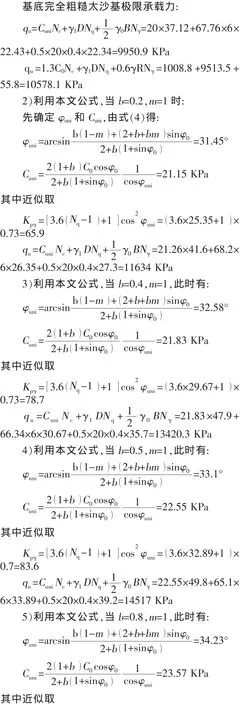

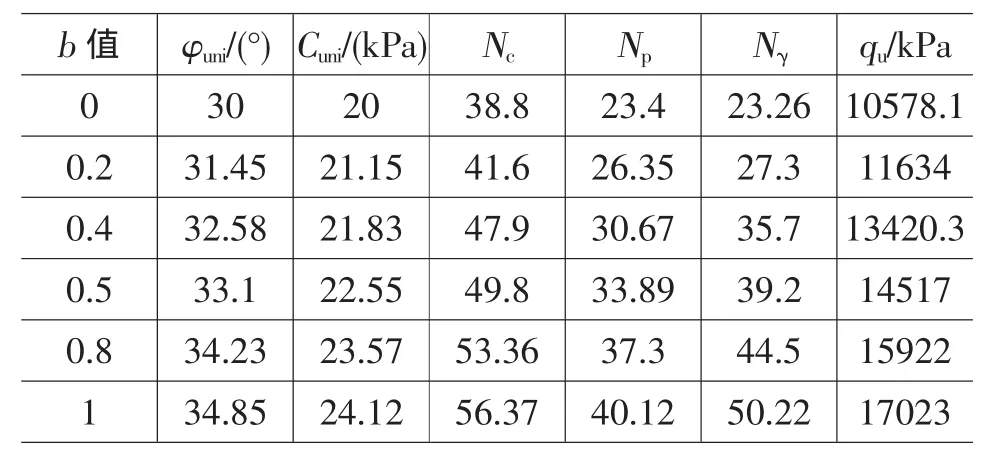
表1 基底完全粗糙時不同b值樁基地基承載力計算結果
應用Matlab軟件做出基底完全粗糙時qu隨b值的變化曲線見圖5。
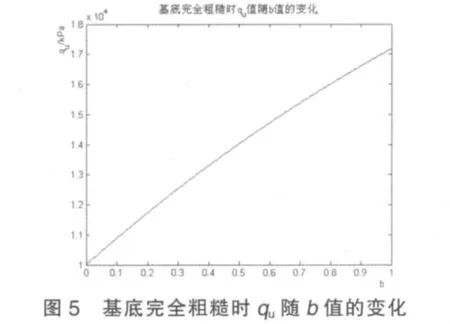
基底完全光滑的情況:
1)利用太沙基公式
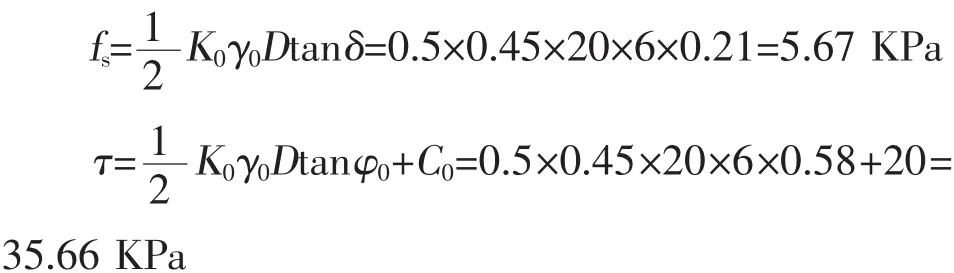
基底完全粗糙太沙基極限承載力:
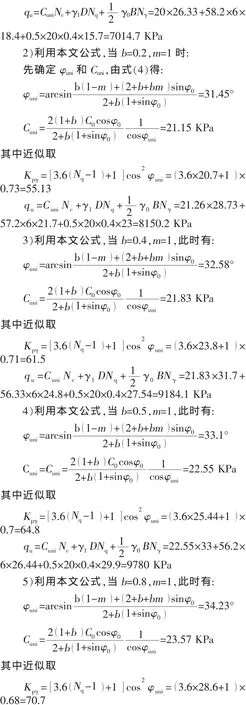

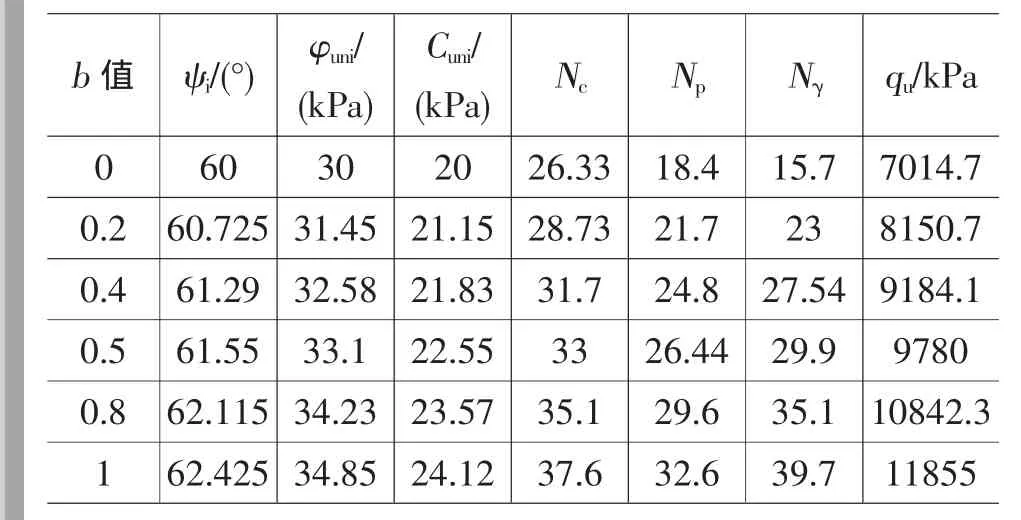
表2 基底完全粗糙時不同b值樁基地基承載力計算結果
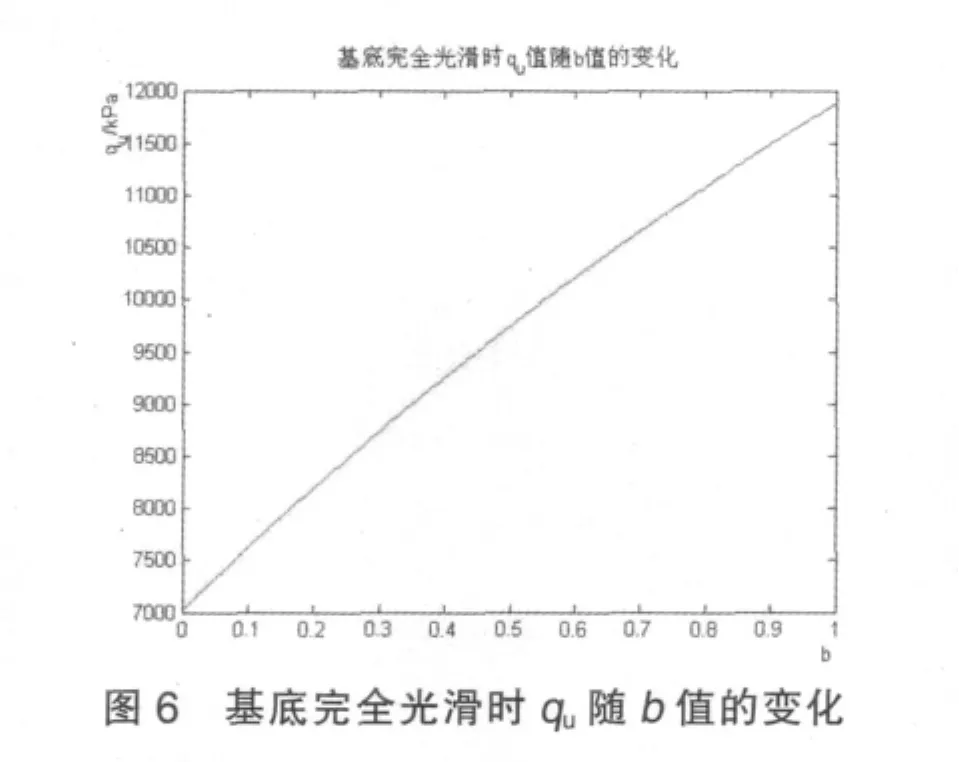
應用Matlab軟件做出基底完全光滑時qu隨b值的變化曲線見圖6。
5 結論
1)基于Mohr-Coulomb準則的太沙基樁基極限承載力,由于沒有考慮中間主應力的影響,其結果最小,由算例知在基底完全粗糙和完全光滑的條件下由統一強度理論計算的結果隨b的增大而增大,當b=0時即為Mohr-Coulomb準則,當b=1時即為雙剪強度理論。
2)在實際工程中基底既不是完全粗糙也不是完全光滑的,即ψ角是介于φ和φ/2+45°之間的,但根據兩種極端情況下得出的結果,不難得出實際工程中樁基極限承載力亦隨b的增大而增大。
3)利用統一強度理論建立了樁基極限承載力的統一解形式,利用此解可以合理的得出不同b值對應的相應解,可以充分發揮材料自身的承載能力,對實際工程有重要意義。
[1]雍景榮,朱凡,胡岱文.土力學與基礎工程[M].成都:成都科技大學出版社,1995.
[2]周小平,張永興.基于統一強度理論的太沙基地基極限承載力[J].重慶大學學報(自然科學版),2004,27(9):133~136.
[3]周小平,張永興.利用統一強度理論求解條形地基極限承載力[J].重慶大學學報(自然科學版),2003,26(11):109~112.
[4]周小平,黃煜鑌,丁志誠.考慮中間主應力的太沙基地基極限承載力公式[J].巖石力學與工程學報,2002,21(10):1554~1556.
[5]俞茂宏.雙剪理論及其應用[M].北京:科學出版社,1998.
[6]俞茂宏,楊松巖,劉春陽,劉劍宇.統一平面應變滑移線場理論[J].土木工程學報,1997,30(2):14~26.
[7]錢家歡,殷宗澤.土工原理及計算(第二版)[M].北京:中國水利水電出版社,1996.


