行星齒輪傳動齒根動應力計算

蔣立冬，李應生，朱振榮，陳營利

（中國船舶重工集團公司第七○三研究所，黑龍江哈爾濱 150078）

0 引言

齒根彎曲應力是齒輪最重要的強度性能之一，它的大小直接影響齒輪的使用壽命和安全［1］。目前多采用有限元軟件Ansys等對齒輪進行接觸仿真得到齒根應力值［2－3］。但對于功率分流式行星傳動的齒輪，其重合度較大，同時嚙合的齒數多達4～6個。為了計算1個齒由進入嚙合到退出嚙合全過程中齒根應力的變化，對于重合度大于4的齒輪，計算至少要涉及到9個不同的齒。對于人字齒輪，1個嚙合位置就是18個齒。對于有3個嚙合位置的太陽輪，就至少要對54個齒進行有限元網格密劃。而計算量要涉及32～38個嚙合位置。因此，若要采用完整模型進行齒根動應力的計算，其計算量將十分龐大。本文通過研究與對比計算后發現，可以在保證計算精度的條件下，通過適當簡化計算模型，減少有限元計算規模，實現齒根動應力的計算。

1 齒根動應力計算方法

在進行齒根動應力計算時，首先需要確定人字齒輪嚙合過程中的齒向載荷分布和齒間載荷分布，文中主要計算齒輪在靜載作用下的齒根應力變化，故首先根據系統靜力學分析確定1對齒輪傳動中所傳遞的總法向載荷。

在確定了齒輪嚙合所傳遞的法向載荷后，根據輪齒的幾何參數關系和齒輪的結構，分析在1個嚙合周期內的若干對接觸線的位置以及相應位置輪齒的剛度。再根據上述分析結果，進一步得到輪齒的嚙合剛度，以及在各嚙合位置相應的接觸線間載荷的分配與每條接觸線上載荷的分布情況，為齒輪的強度計算提供較為準確的加載位置和齒面載荷分布。

計算出的各嚙合位置相應的接觸線間載荷的分配與每條接觸線上載荷的分布，利用Ansys中的APDL語言形成載荷文件［4］，在計算時導入相應的載荷文件從而在輪齒接觸面上尋找載荷作用點附近的節點進行加載計算。

由于齒輪的重合度不是整數，故同時參與嚙合的齒的個數是交替變化的。在簡化計算時，考慮到某1個輪齒的齒根應力主要受到自身的嚙合力以及與其左右相鄰的2個齒上嚙合力影響，而與其相鄰較遠的齒上的嚙合力對這個齒的齒根應力的影響可以忽略。因此，本文中計算齒根應力的模型是只保留幾個齒進行加載，而忽略其他參與嚙合齒上的載荷。

2 功率分流行星傳動齒根動應力計算

2.1 模型的構建

現以功率分流行星齒輪傳動系統差動級太陽輪為例，說明齒根動應力的計算過程。

在功率分流式行星傳動中，差動級太陽輪與3個行星輪進行嚙合。為了減少計算量，在建立模型時對太陽輪進行了剃齒簡化，具體是把與聯軸器聯接的直齒抹平至分度圓;與行星輪嚙合的人字齒只保留5個齒，并將這5個齒剃齒至分度圓，其余的齒抹平到分度圓，但只在中間3個齒上加載，劃分網格時也只對中間的3個齒進行密化，其余2個齒保證了齒輪模型的完整性，簡化后的實體模型如圖1所示。

圖1 簡化后的差動級太陽輪實體模型Fig.1The model of the sun gear in the differential stage

設置材料參數:彈性模量E=2.06×105MPa，材料密度ρ=7 900 kg/m3，泊松比μ=0.3。

為了降低計算規模和提高計算效率，太陽輪網格劃分的具體措施是，在加載的3個輪齒齒面設定盡可能小的單元尺寸，將受載輪齒的齒根處也設定盡可能小的網格單元尺寸，從而劃分較密的網格。整個結構統一采用四面體單元Solid45單元，所生成的太陽輪有限元網格如圖2所示。

圖2 差動級太陽輪有限元模型Fig.2The finite element model of the sun gear in the differential stage

2.2 邊界條件

對行星齒輪傳動系統進行靜力學分析，得到差動級太陽輪1個齒在嚙合過程所傳遞的法向載荷歷程如圖3所示。

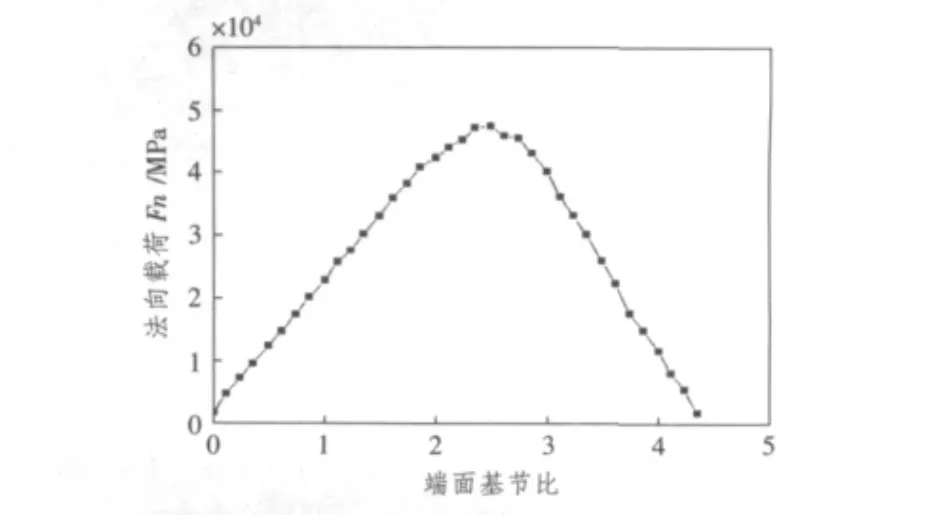
圖3 太陽輪在嚙合過程中單齒上的法向載荷歷程Fig.3The normal force of single tooth on sun gear in meshing process

根據齒面載荷分布計算程序確定的接觸線載荷分布值和載荷作用點坐標，在嚙合齒面上施加力邊界條件。在載荷作用點相應的就近節點上施加載荷時，把作用力分解到x，y，z三個方向上，如圖4所示。

由于對太陽輪加載時只對1個嚙合位置加載，而另外2個嚙合位置施加固定約束，故只考慮同1個行星嚙合位置上齒輪的嚙合過程。改變力邊界條件，實現1個齒從嚙入到嚙出的加載過程，可以在Ansys中進行坐標變換，并讀取載荷力文件在載荷作用點相應的就近節點上加載計算。

圖4 嚙合力施加示意圖Fig.4The loaded meshing force

由于該太陽輪是和3個行星輪進行嚙合，對于簡化后的模型，在另2個嚙合處施加固定約束，同時這兩處固定約束是變化的，可以在Ansys中把坐標進行旋轉變換，即依次把坐標系繞z軸分別順時針旋轉360°，即得到后面幾處和行星輪嚙合的固定約束位置。再通過變換把節點坐標和節點的各載荷分量轉化到相應坐標系下，再依次進行加載。選擇1個嚙合位置的位移邊界條件如圖5所示。

圖5 太陽輪的力邊界條件示意圖Fig.5The constrained force of the sun gear

2.3 齒根動應力計算結果

將上述有限元模型實施求解操作后，可以得到1個齒在嚙合過程中齒根的應力，同時可以得出齒根處應力最大值的變化情況，以及齒根應力最大值對應的節點在各個嚙合位置的應力。由于齒輪的齒根斷裂應力是對應著徑向應力σr，因此，應用最大的徑向應力與極限應力對比，可以判斷輪齒是否滿足強度條件。計算結果表明，太陽輪的齒根最大徑向應力為79.561 MPa，出現在四齒嚙合時的齒根處（見圖6）。

在計算過程中，齒輪模型都只對3個齒進行加載，所以在研究1個齒上的應力時，對象是中間齒上的應力結果。在靜載荷作用下，對于1個齒從嚙合進入到退出的過程中，所施加的法向載荷變化如圖5所示，通過計算可以得出太陽輪嚙合過程齒根處的最大徑向應力變化如圖7所示，圖中的數字5和4分別表明處于五齒嚙合區和四齒嚙合區。

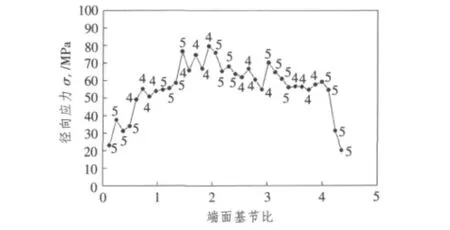
圖7 嚙合過程中太陽輪齒根處最大徑向應力的變化Fig.7The max radial stress on sun dedendum in the meshing process

嚙合過程中變化的徑向應力最大值所在的點的徑向應力歷程如圖8所示，可以反映出齒根處應力最大值一點在嚙合過程中的應力變化情況。該文的計算方法與采用傳統計算方法得出的齒輪彎曲應力值很吻合，說明本文的計算方法是正確的［5］。

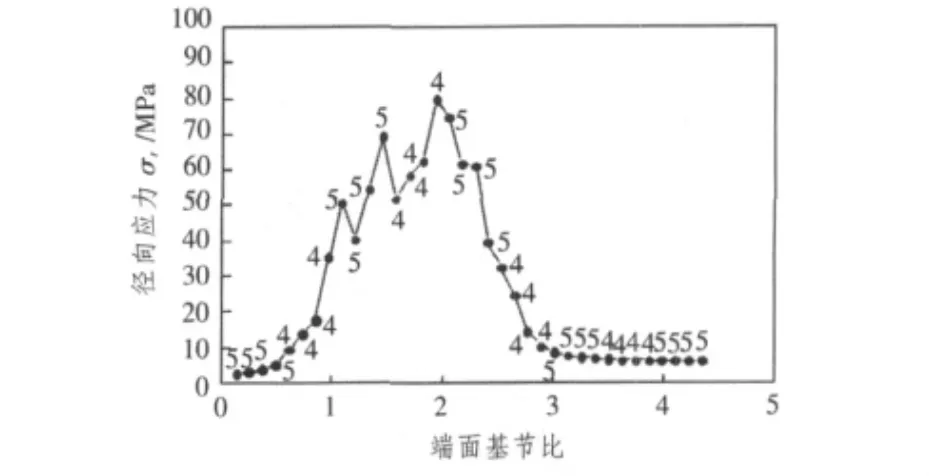
圖8 徑向應力最大值點在嚙合過程中的應力值Fig.8The stress value of the position with max stress in the meshing process

3 結語

本文針對功率分率行星齒輪傳動齒輪重合度大，齒根應力計算工作量大的問題，對齒根動應力的計算問題進行了詳細研究。首先根據輪齒的幾何參數關系和齒輪的結構，分析在1個嚙合周期內若干對接觸線的位置，以及在各嚙合位置相應的接觸線間載荷的分配與每條接觸線上載荷的分布情況;然后利用Ansys

中的APDL語言形成載荷文件，在計算時導入相應的載荷文件從而在輪齒接觸面上尋找載荷作用點附近的節點進行加載計算。本文的計算方法可以精確、快速地得到1個齒在嚙合過程中齒根的動應力。

［1］馮守衛，王守宇，張偉社，等．齒輪齒根應力輪齒撓度嚙合剛度和端面載荷系數的研究［J］．機械傳動，2005，29 （3）:12－15．

FENG Shou-wei，WANG Shou-yu，ZHANG Wei-she，et al． Study on tooth root stress，tooth deflection，mesh stiffness and transverse load factors of gears［J］．Journal of Mechanical Transmission，2005，29（3）:12－15．

［2］錢學毅，郭波，鄒麗梅．基于ANSYS和Pro/E的直齒圓錐齒輪齒根應力有限元分析［J］．機械傳動，2006，30（5）: 66－67．

QIAO Xue-yi，GUOBo，ZOULi-mei．Finiteelement analysis of tooth root stress for straight bevel gear based on ANSYSandPro/E［J］．JournalofMechanical Transmission，2006，30（5）:66－67．

［3］肖望強，李威，李梅．雙壓力角非對稱齒廓齒輪齒根彎曲應力的有限元分析［J］．北京科技大學學報，2006，28 （6）:570－575．

［4］王國強．實用工程數值模擬技術及其在ANSYS上的實踐［M］．西安:西北工業大學出版社，1999．

WANG Guo-qiang．Technology of practical engineering numerical simulation and application on Ansys［M］．Xi'an: Xi'an Northwestern Polytechnical University Press，1999．

［5］朱孝錄．齒輪傳動設計手冊［M］．北京:化學工業出版社，2005．