復式河槽平均局部阻力系數的研究
趙紅旭,關雅迪
(1.國電電力發展股份有限公司,黑龍江牡丹江157000;2.大連大學,遼寧大連116622)
0 引言
SKM方法是以平均水深的N—S方程為基礎提出的,因其可較準確反應漫灘水流的現象而被廣泛應用,其解析解計算式中有3個重要的參數分別為渦黏系數λ、二次流項Γ及達西阻力系數f。其中達西阻力系數f不同于傳統達西公式,通過其定義(f=8τb/ρUd2)及許多學者[1,7-10]的研究發現將SKM法的達西阻力系數稱為平均局部阻力系數更為合適。達西阻力公式在知道復式河槽各區斷面平均流速時可準確推算各區流量及總流量,但在實際測量中由于灘槽摻混作用很難準確測得各區斷面平均流速,因此要準確得到各區達西阻力系數就變得很困難。所以在實際測量中可用SERCFCF系列試驗的方法,用LDV測垂向點流速Ui,用普雷斯通管測量對應垂線的床面剪切力τbi,后用上述定義式求得局部阻力系數再平均求得復式河槽各區平均局部阻力系數,修正后可準確推求總過流量。
許多學者(Shiono[1],Knight[2-3],Rameshwaran[4],Rezaei[5],Ervine[6],Liao[7-8],Tang[9-10],槐 文 信[11-12],楊 中華[13-14]及許唯林[15]等)在研究SKM法時均采用這一平均局部阻力系數。Shiono和Knight[1]在提出SKM方法時即給出了平均局部阻力系數計算式并擬合了主槽與灘地阻力系數與相對水深的關系式。Liao[7-8]研究了平均局部阻力系數對于SKM法解析解的影響。Rameshwaran[4]發現主槽和灘地的平均局部阻力系數與相對水深存在一定關系。綜上可得,在研究SKM法時必然會涉及到平均局部阻力系數的計算,因此,探索其規律就顯得尤為重要。
本文重點研究復式河槽各區的平均局部阻力系數,探討各區平均局部阻力系數的相互關系,進而通過反算推求斷面總過流能力,并推求平均局部阻力系數與達西公式的轉換關系。
1 局部阻力系數分析與計算
本文運用SERC—FCF的水槽試驗資料(詳見表1),給出了每個系列各區局部阻力系數平均值與相對水深(Dr=(H-h)/H)的關系(如圖3~圖5)。各區平均局部阻力系數值采用下式計算為:

式中:fij、τbij和Udij分別為第i區j點的局部阻力系數、局部剪切力和局部平均流速;ρ為水體密度。
復式河槽斷面形態如圖1所示,其中可劃分為4個區域:主槽區(4區)、摻混區(3區)、灘地區(2區)和灘地邊坡區(1區)。這里給出(1)式計算得到的FCF0804組資料主槽和灘地局部阻力系數見圖2。
各系列灘地平均局部阻力系數f2隨相對水深Dr的關系如圖3,隨著Dr增大,f2減小。試驗資料表明f2與相對水深為0.25的f2(0.25)之比與Dr滿足乘冪關系,如圖4。關系式如下

主槽與灘地平均局部阻力系數之比f4/f2與Dr滿足拋物線分布,如圖5所示。可以看出它們的比值滿足二次函數,其關系式如下

在邊壁區平均局部阻力系數f1受到邊壁影響,但圖6表明,f1與f2可認為相等。圖7說明主槽邊坡平均局部阻力系數f3與(f2+f4)/2有一定線性關系,可用下式計算


表1 復式河槽系列試驗斷面形態資料
2 流量估算
在推求復式河槽過流能力時,用各區達西阻力系數推求整個過留斷面流量的方法已被證明具有較高精度[16]。其計算公式為:

本文用平均局部阻力系數來反算復式河槽過流能力。各區流量可表示為:

式中:Qi為第i區過流量;Ai為第i區過流斷面面積;fi為第i區平均局部阻力系數;其余參數同上。
總過流量為

根據前述的各區阻力系數關系求得SREC-FCF03的資料在不同相對水深下的總過流量。實測流量和計算流量如圖8所示。可以看出計算值較實測值大,說明平均局部阻力系數較(5)式計算的阻力系數有一定偏差,需對其值進行修正。

圖1 復式河槽斷面形態圖

圖2 主槽和灘地平均局部阻力系數f4和f2(FCF0804)

圖3 灘地平均局部阻力系數隨相對水深的變化

圖4 灘地平均阻力系數f2和f2(0.25)之比與相對水深的變化關系圖

圖5 主槽和灘地平均阻力系數隨相對水深的變化圖

圖6 灘地邊坡區與灘地區局部阻力系數的關系圖

圖7 主槽邊坡區與主槽和灘地區平均阻力系數的關系圖

圖8 計算流量與實測流量比較圖

圖9 主槽區阻力系數與平均局部阻力系數隨相對水深的變化

圖10說明灘地阻力系數f2與平均阻力系數表現出一定線性關系,經擬合得
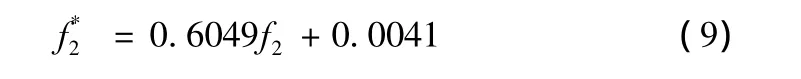
將(1)式計算出的平均局部阻力系數用(8)(9)式進行修正,再用修正后的平均局部阻力系數反算過流量,如圖11所示,從圖中看出修正后的平均阻力系數估算斷面過流量比較準確,平均相對誤差為1.4%。
3 結論
1)本文研究基于SERC—FCF的系列試驗資料,結論可運用于水槽試驗中,在天然河道中的平均局部阻力系數需用實測資料進一步率定。
2)灘地平均局部阻力系數隨相對水深的增加而減少,將其無量綱后于相對水深符合成乘冪關系,主槽和灘地平均阻力系數之比與相對水深滿足二次函數;灘地邊坡和灘地平均阻力系數相等;主槽邊坡平均阻力系數可用主槽和灘地平均阻力系數函數表示。
3)灘地平均阻力系數與達西阻力系數滿足線性關系,而主槽兩值之比呈對數分布。
4)用平均局部阻力系數推算的斷面總過流量較實測值偏大,經過修正后,其值推求的計算流量與實測值吻合較好,平均相對誤差為1.4%。

圖10 灘地區阻力系數與平均局部阻力系數的關系圖
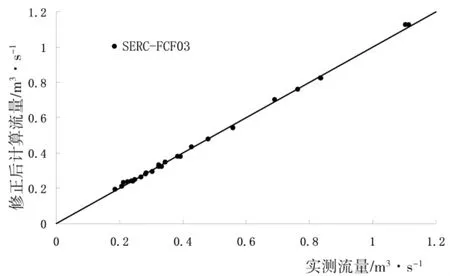
圖11 修正后的計算流量和實測流量比較圖
[1]K Shiono,D Knight.Turbulent open-channel flows with variable depth across the channel[J].Journal of Fluent Mechanism,1991,222(5):617-646.
[2]D Knight,M Omran and Xiaonan Tang.Modeling depth-averaged velocity and boundary shear in trapezoidal channels with secondary flows[J]. Journal of hydraulic engineering ASCE,2007,133(1):39-47.
[3]D Knight,B Abril.Refined calibration of a depth-averaged model for turbulent flow in a compound channel[C].Process Institution of Civil Engineers,Water,Maritime and Energy,London,paper 11017,118,151-159.
[4]P Rameshwaran,K Shiono.Quasi two-dimensional model for straight overbank flows through emergent vegetation on floodplain[J].Journal of Hydraulic Research,2007,45(3):302-315.
[5]B Rezaei,D Knight.Application of the Shiono and Knight Method in compound channels with non-prismatic floodplain[J].Journal of Hydraulic Research,2010,47(6):716-726.
[6]A Ervine,K Babaeyan-Koopaei and R Sellin.Two-dimentional solution for straight and meandering overbank flows[J].Journal of hydraulic engineering ASCE,2000,126(9):653-669.
[7]Huasheng Liao,D Knight.Analytic Stage-discharge formulas for flow in straight prismatic channels[J].Journal of hydraulic engineering ASCE,2007,133(10):1111-1122.
[8]Huasheng Liao,D Knight.Analytic Stage-discharge formulas for flow in straight trapezoidal open channels[J].Advances in water resources,2007,(3):2283-2295.
[9]Xiaonan Tang,D Knight.Analytical models for velocity distribution in open channel flows[J].Journal of Hydraulic Research,2009,47 (4):418-428.
[10]Xiaonan Tang,D Knight.Lateral depth-averaged velocity distributions and bed shear in rectangular compound channels[J].Journal of hydraulic engineering ASCE,2008,134(9):1337-1342.
[11]槐文信,耿川,曾玉紅,等.部分植被化復式河槽紊流時均流速分布解析解[J].應用數學和力學,2011,32(4):437-445.
[12]槐文信,徐治剛,楊中華等.部分植被花復式河道水流的二維解析解[J].應用數學和力學,2008,29(8):976-983.
[13]楊中華,高偉.考慮灘槽相互作用的漫灘水流二維解析解[J].四川大學學報:工程版,2009,41(5):42-47.
[14]楊中華,高偉,槐文信.漫灘水流二次流項系數研究[J].應用數學和力學,2010,31(6):681-690.
[15]許唯林.復式河道漫灘水流計算方法研究[J].水利學報,2002 (6):21-28.
[16]楊克君,曹叔尤,劉興年.復式河槽阻力系數及過流能力計算[J].水科學進展,2005,16(1):23-27.

