反艦導彈自適應模糊滑模控制系統(tǒng)設計

王朝轟，李增榮，賀建彬

（1.91115部隊，浙江 舟山 316000；2.海軍裝備部駐上海地區(qū)軍事代表局，上海 200083；3.海軍工程大學兵器工程系，武漢 430033）

新型反艦導彈的彈道越來越復雜，在建立其彈道模型時，傳統(tǒng)的姿態(tài)控制方法已經(jīng)不能滿足設計要求，需要尋找新的途徑。尤其是，高低結(jié)合彈道的引入使得彈道設計的難度大大增加。然而，過載控制是一種比較簡單、可靠的控制方法，更為適用于新型反艦導彈。

文獻[1]將神經(jīng)網(wǎng)絡應用于自適應反饋線性化非線性系統(tǒng)；文獻[2]利用神經(jīng)網(wǎng)絡控制未知動態(tài)特性的非線性系統(tǒng)；文獻[3]運用動態(tài)逆的雙階段設計方法設計了導彈的逆控制器，并利用有效信息對逆控制器進行在線補償，實現(xiàn)了對導彈的控制；文獻[4]提出了一種基于神經(jīng)網(wǎng)絡的導彈魯棒動態(tài)逆控制方法，利用RBF神經(jīng)網(wǎng)絡逼近導彈慢模態(tài)數(shù)學模型，魯棒控制器用于減弱模型不確定性及神經(jīng)網(wǎng)絡的逼近誤差對跟蹤精度的影響，該控制器設計可以保證閉環(huán)系統(tǒng)的穩(wěn)定性。文獻[5-6]運用自適應模糊滑模設計，對導彈末端機動引導律進行了探討，仿真表明了其方法的正確性和有效性。但文獻[1-4]諸方法雖然達到了預期的效果，但本質(zhì)上都屬于姿態(tài)控制方法。相對于過載控制方法，傳統(tǒng)姿態(tài)控制方法使導彈機動性能變差。因此，直接對導彈過載進行控制的過載控制方法將有利于提高導彈的機動能力。

本文針對反艦導彈的過載控制系統(tǒng)設計問題，提出了一種自適應模糊滑模控制系統(tǒng)設計方法。通過Lyapunov 穩(wěn)定性分析，證明了此閉環(huán)系統(tǒng)的所有誤差信號均有界且指數(shù)收斂至原點的有界鄰域內(nèi)，且仿真結(jié)果驗證了該方法的有效性。

1 反艦導彈過載控制模型

以氣動外形呈軸對稱分布的導彈為例，研究其俯仰通道線性動力學模型[7]：

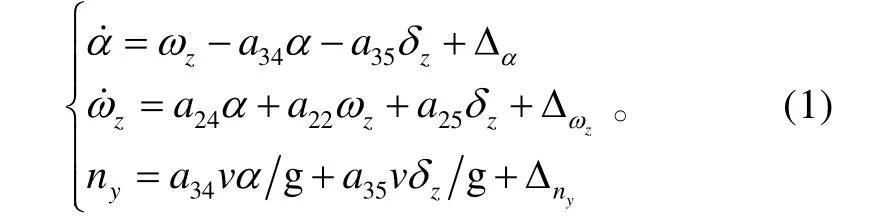
式(1)中：α為迎角；ωz為俯仰角速度；δz為俯仰舵偏角；ny為法向過載；v為飛行速度；g為重力加速度；a22、a24、a25、a34和a35均為導彈的動力系數(shù)；Δα、Δzω和Δny均為模型線性化過程中的不確定項。

考慮舵系統(tǒng)的一階動態(tài)特性為：

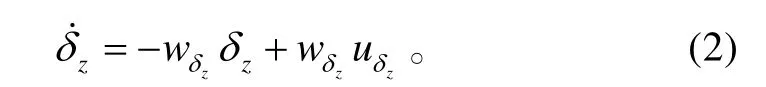
式(2)中：wzδ為俯仰舵系統(tǒng)的帶寬；uzδ為控制輸入。

進行如下的坐標變換：

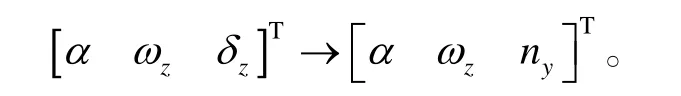
聯(lián)立式(1)、(2)可得：

針對俯仰通道模型(3)，控制目標為：在給定的法向過載指令 nyc作用下，設計合理的控制律uzδ，使得導彈的實際法向過載 ny跟蹤 nyc，且迎角α和俯仰角速度ωz都收斂到理想狀態(tài)。為了實現(xiàn)此控制目標，將式(3)變換為標準的三角形式，定義可逆的狀態(tài)變換矩陣T為：

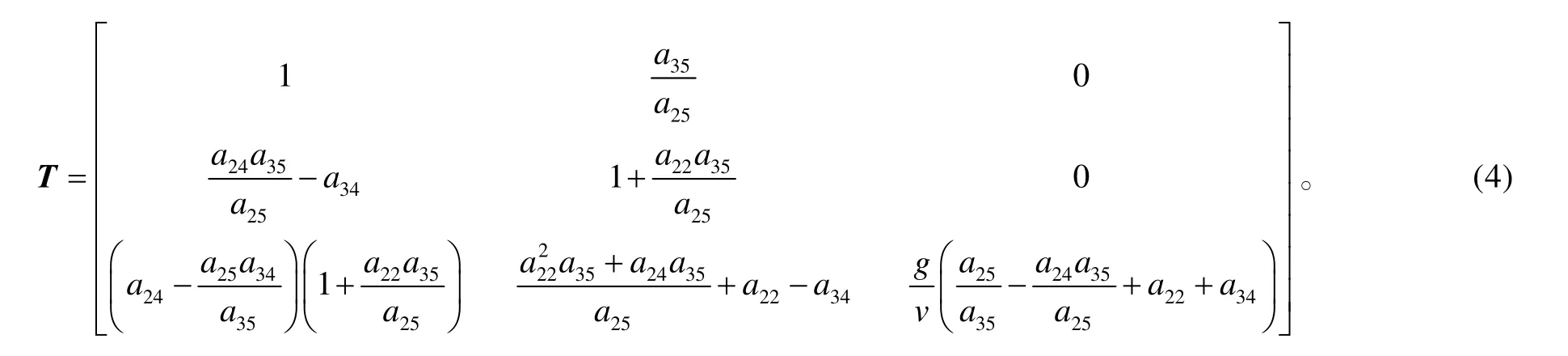
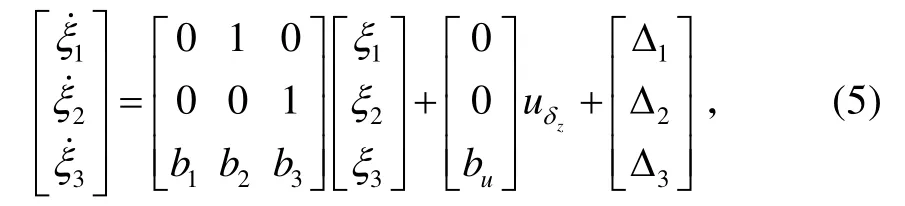
式中各參數(shù)的取值參見文獻[4]。

由于狀態(tài)變換矩陣T是可逆的，則系統(tǒng)(5)與系統(tǒng)(3)屬于等價變換。以下將針對系統(tǒng)(5)，設計和分析俯仰通道的過載控制系統(tǒng)。

2 反艦導彈過載控制系統(tǒng)設計

2.1 問題闡述

假設1：存在未知的上界值r1、r2和r3，使得系統(tǒng)的不確定項 Δ1、Δ2和Δ3滿足：

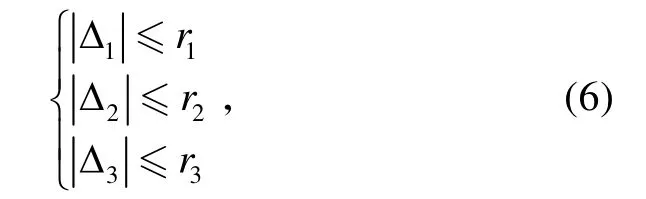
針對等價變換后的俯仰通道過載控制模型(5)，采用反演設計方法和自適應模糊控制方法進行設計。定義被控對象(5)的狀態(tài)誤差為：

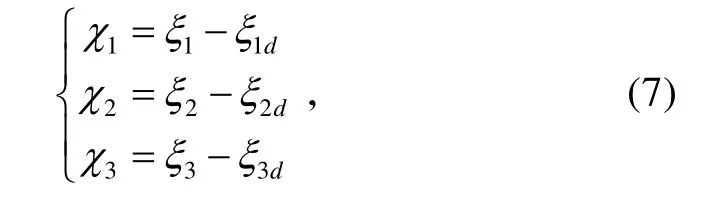
式中，ξ1d、ξ2d和ξ3d為系統(tǒng)期望的狀態(tài)軌跡，ξ1d由期望的過載信號 nyc濾波得到，ξ2d和ξ3d分別由式(13)、(29)定義。

由式(5)、(7)，可得狀態(tài)誤差的動態(tài)方程分別為：

2.2 設計步驟

1)考慮系統(tǒng)(8)，對于期望狀態(tài)的微分信號ξ1d采用模糊邏輯系統(tǒng)給出[8-11]，采用俯仰通道期望的過載信號 nyc和狀態(tài)變量α、ωz、ny作為此模糊邏輯系統(tǒng)的輸入信號，應用模糊邏輯系統(tǒng)具有的任意逼近能力，估計出信號。

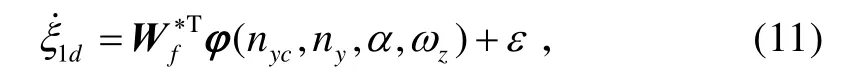
對于期望狀態(tài)ξ1d的獲取，可以直接對微分信號進行積分即可得到。

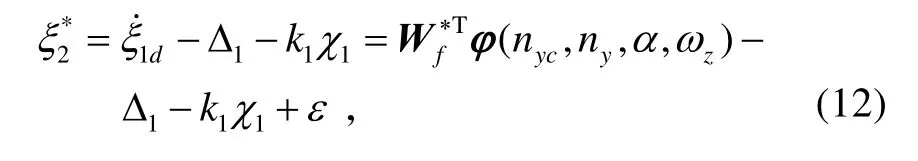
將ξ2作為式(8)的虛擬控制量，則存在一個理想的虛擬控制量：使得其中 k1＞0為設計參數(shù)。由于是得不到的，故選取期望的虛擬控制量為：

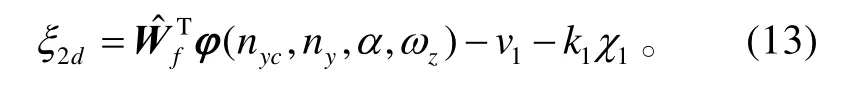
針對系統(tǒng)(8)，選取Lyapunov函數(shù)為：

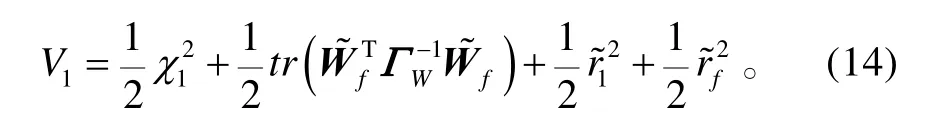
對V1求導，并將式(8)、(11)、(13)代入式(14)，可得：

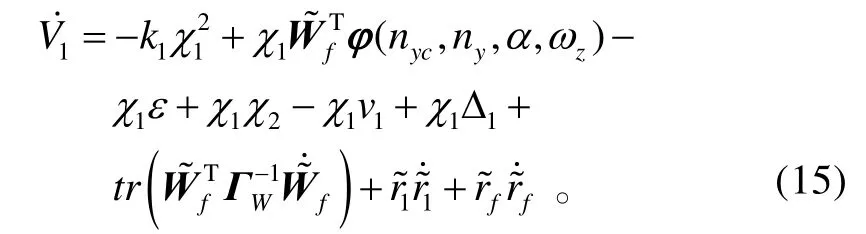
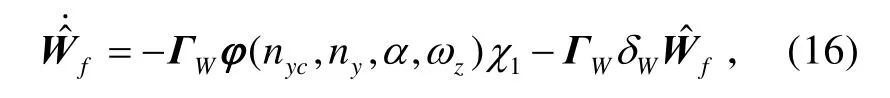
式中，δW＞0為設計參數(shù)。

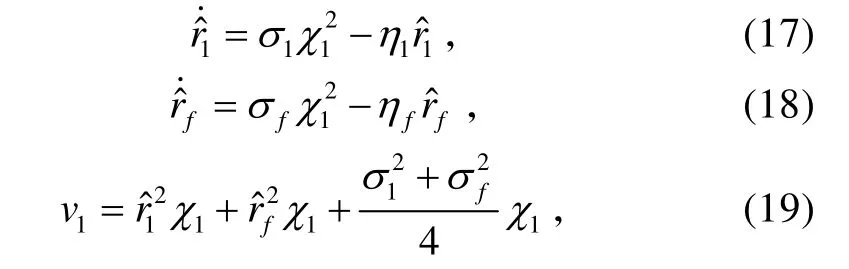
式中，σ1＞0、η1＞0、σf＞0和ηf＞0為設計參數(shù)。

將式(16)～(19)代入式(15)，可得：

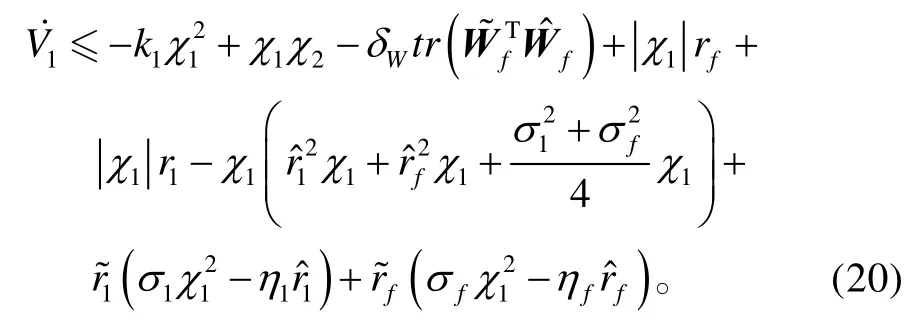
由于

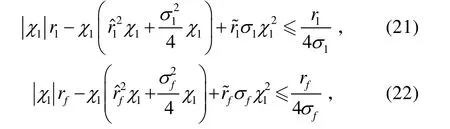
所以，有

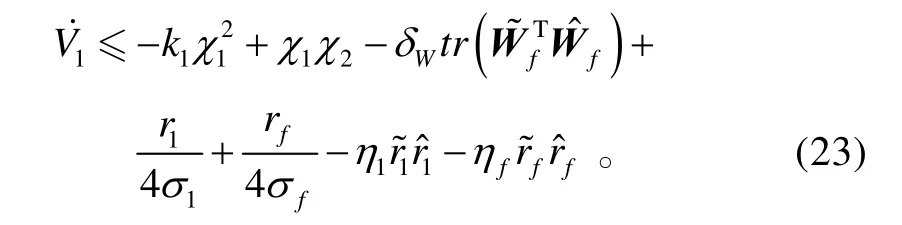
考慮到

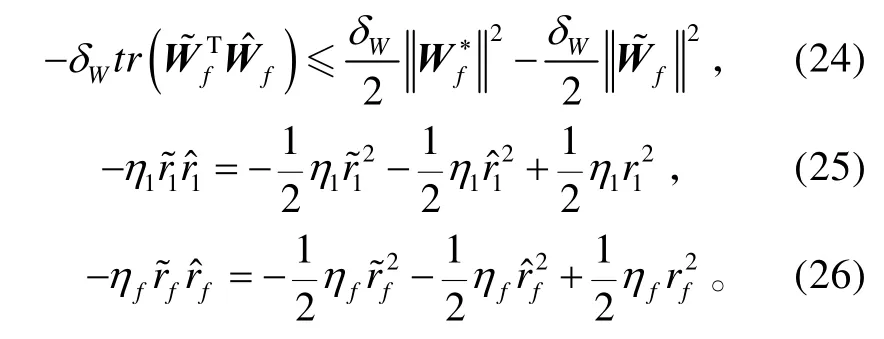
將式(24)～(26)代入式(23)，可得：

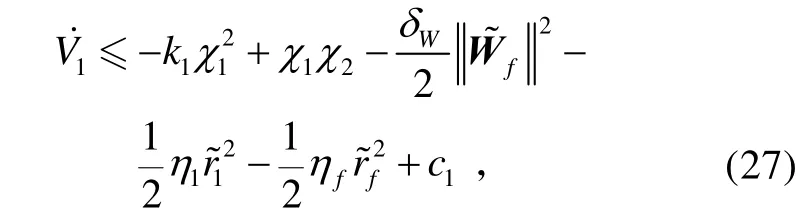
2)考慮系統(tǒng)(9)，將ξ3作為式(9)的虛擬控制量，則存在一個理想的虛擬控制量：

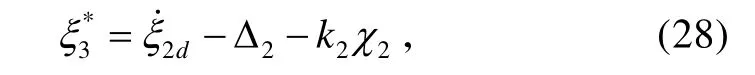
3ξ是得不到的，故選取期望的虛擬控制量為：

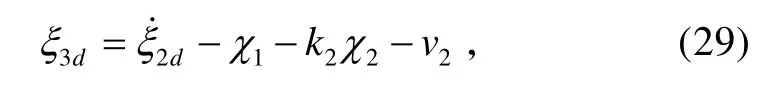
式中，v2為引入的魯棒項，如式(33)所示。

針對系統(tǒng)(9)，選取Lyapunov函數(shù)為：

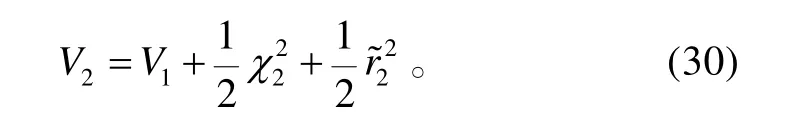
對V2求導，將式(9)代入式(30)，且考慮到假設1，可得：

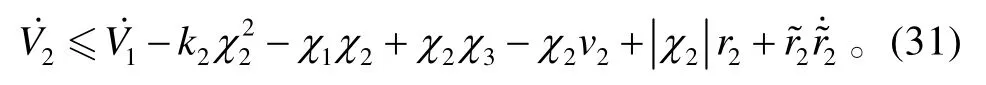
式中，σ2＞0、η2＞0為設計參數(shù)。

將式(32)、(33)代入式(31)，可得：

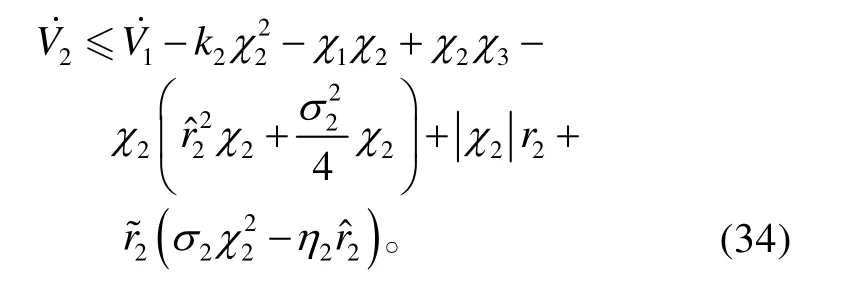
由于

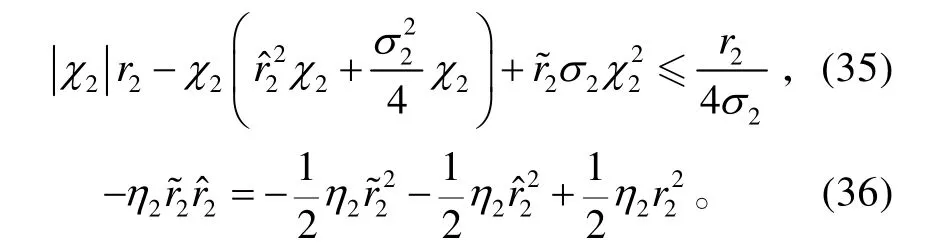
將式(27)、(35)、(36)代入式(34)，可得：

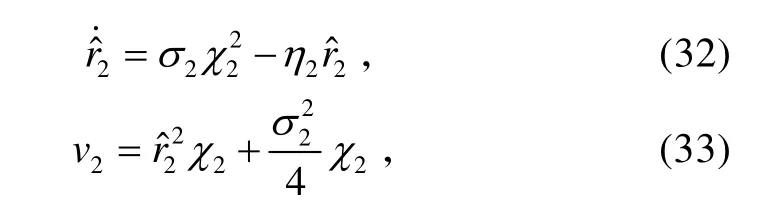
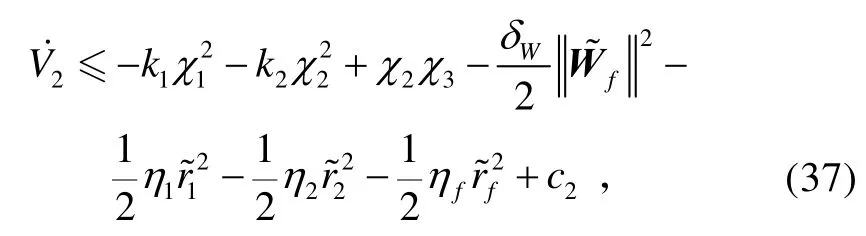
3)考慮系統(tǒng)(9)，其中uzδ為實際控制量，采用滑模控制方法設計控制量uzδ。

設計系統(tǒng)滑模面為：

設計系統(tǒng)的控制量uzδ為：

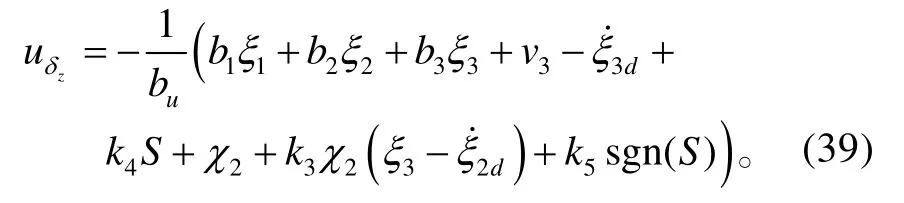
式(39)中：v3為引入的魯棒項，見式(44)；k4＞0、k5＞0為設計參數(shù)；sgn(?)表示符號函數(shù)。

針對系統(tǒng)(9)，選取Lyapunov函數(shù)為：

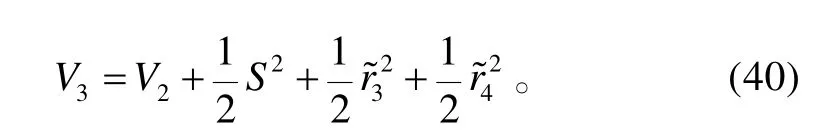
對V3求導，將式(38)、(39)代入式(40)，且考慮到假設1，可得：

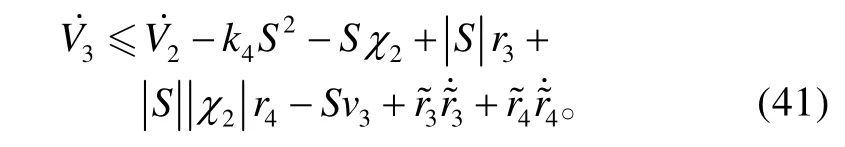
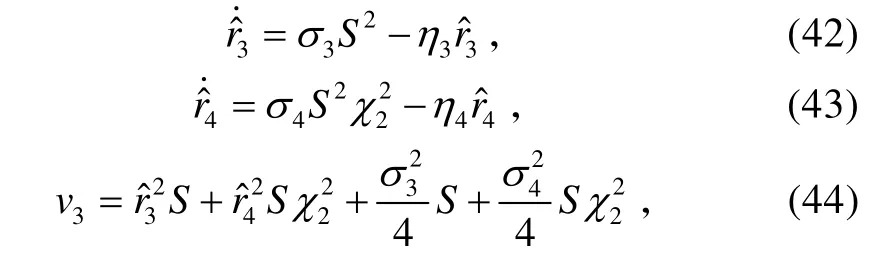
式中，σ3＞0、η3＞0、σ4＞0和η4＞0為設計參數(shù)。

將式(42)～(44)代入式(41)，可得：

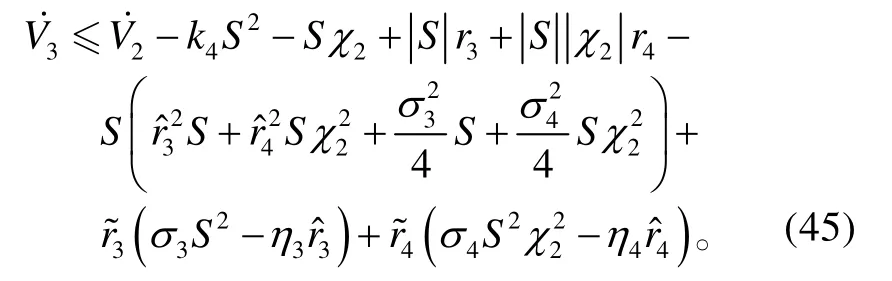
由于

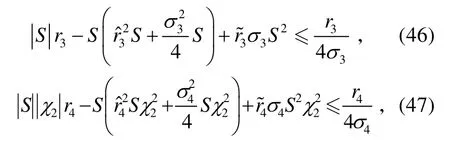
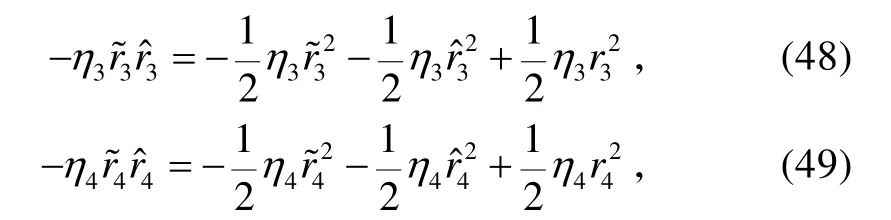
將式(37)、(46)～(49)代入式(45)，可得：

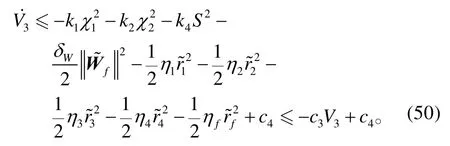
式(50)中：

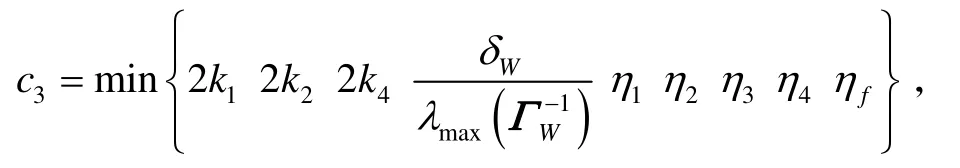
λmax(?)表示矩陣“?”的最大特征根；

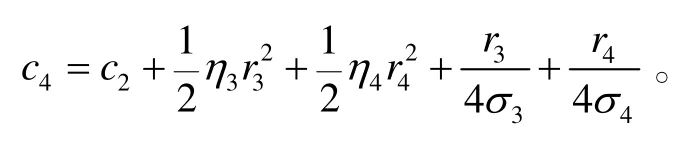
2.3 設計總結(jié)

綜上所述，可得如下結(jié)論。

考慮系統(tǒng)(5)，在假設1的前提下，虛擬控制量和控制量分別采用式(13)、(28)、(39)的形式，模糊邏輯系統(tǒng)的參數(shù)調(diào)節(jié)律采用式(16)的形式，自適應參數(shù)和調(diào)節(jié)律分別采用式(17)、(18)、(32)、(42)、(43)的形式，則系統(tǒng)狀態(tài)跟蹤誤差1χ、2χ和3χ，模糊邏輯系統(tǒng)的參數(shù)估計誤差，以及自適應參數(shù)的估計誤差均有界且指數(shù)收斂至系統(tǒng)原點的一個鄰域：

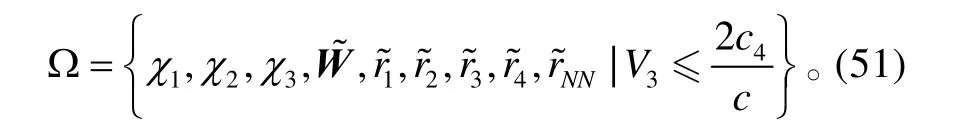
通過式(51)可以看出，調(diào)整1k、k2、k4、δW、η1、η2、η3、η4和ηf的值可以調(diào)節(jié)收斂速度和收斂域的大小。

由于狀態(tài)變換矩陣T是可逆的，系統(tǒng)(5)與系統(tǒng)(3)屬于等價系統(tǒng)，因此，控制量(39)同樣適用于系統(tǒng)(3)。

在實際操作過程中，利用彈上的俯仰加速度計可以測量得到ny信號；利用測速陀螺儀可以得到俯仰角速度信號；對于迎角α的獲取，可以利用加速度計輸出信號 ny與俯仰舵偏角信號δz進行估計，解算公式為將得到的信號矢量經(jīng)過矩陣T的變換，即可得到控制量(39)中所需的狀態(tài)向量

3 仿真分析

采用本文提出的控制方法，對反艦導彈的俯仰通道控制回路進行特征點仿真。

俯仰通道動力學模型如式(2)、(3)所示，假設此模型中不確定項分別為：

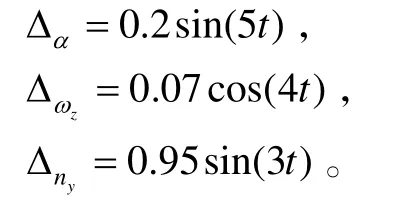
根據(jù)定理1的設計要求，分別選取參數(shù)：

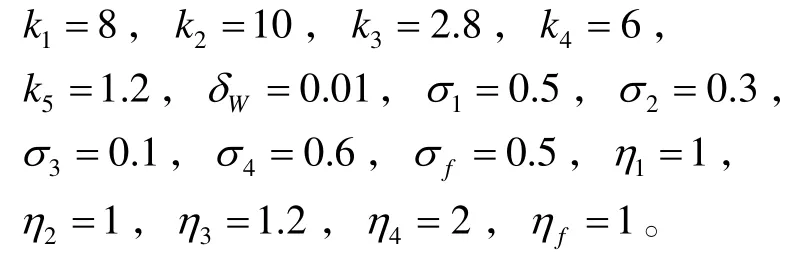
模糊邏輯系統(tǒng)的隸屬函數(shù)為：

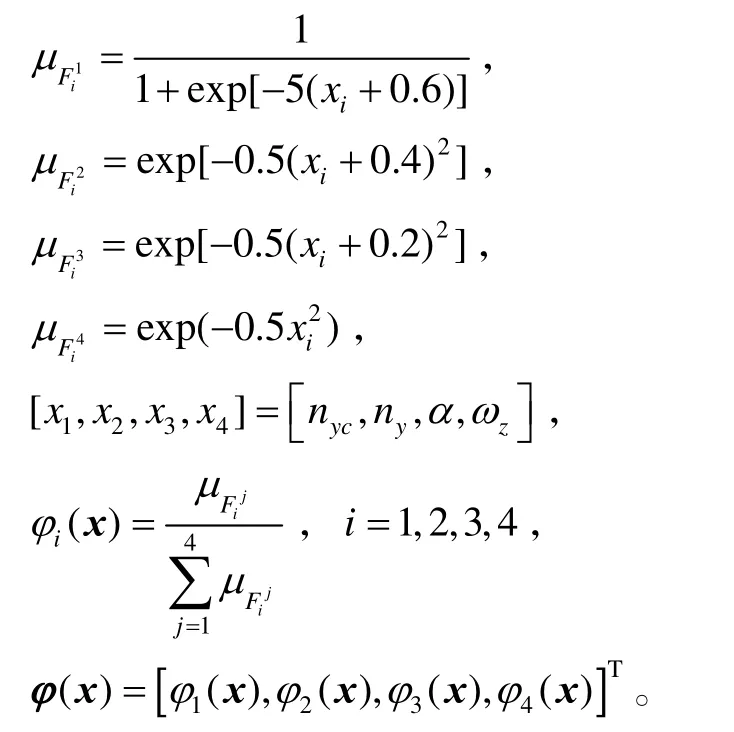
同時，為了削弱滑模控制的抖振現(xiàn)象，對符號函數(shù)sgn(S)進行連續(xù)化處理，以連續(xù)化函數(shù)S (|S|+ε)代替sgn(S)，ε=0.003。

運用上述設計的控制器，得到的仿真結(jié)果分別如圖1～4所示。

在仿真圖2中，虛線為法向過載的指令信號nyc，實線為實際法向過載信號 ny。

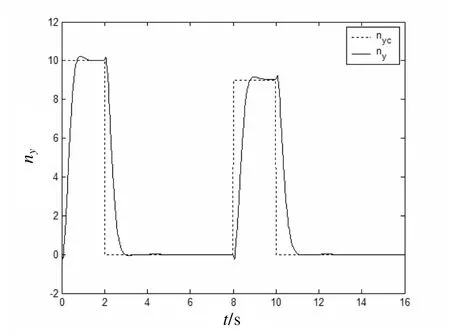
圖1 法向過載 ny仿真曲線

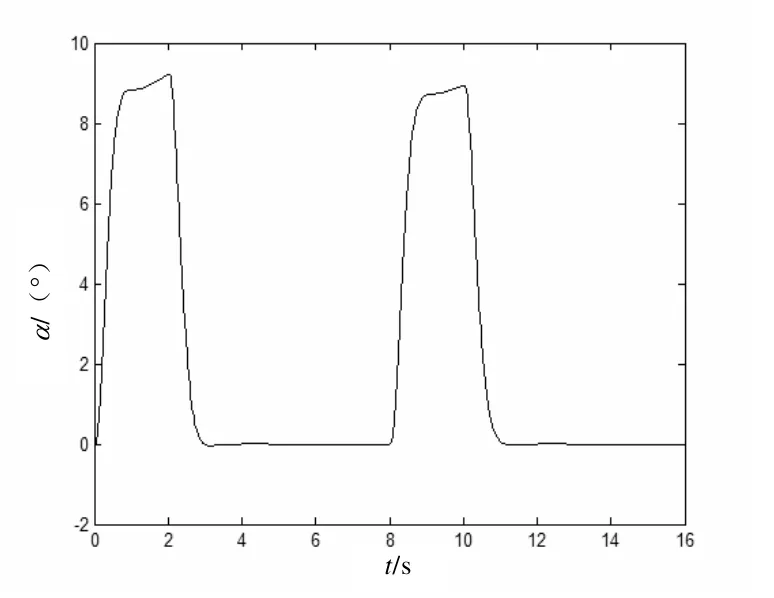
圖2 迎角α仿真曲線

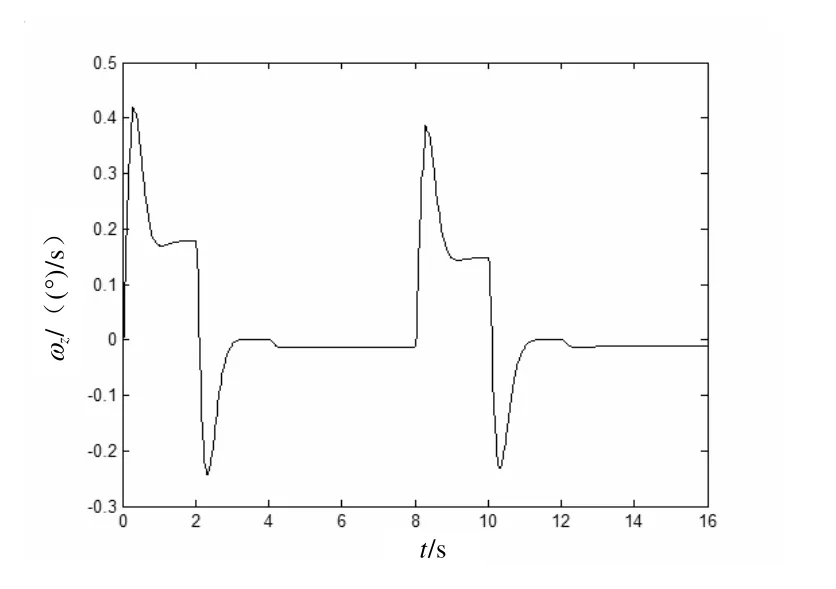
圖3 俯仰角速度ωz仿真曲線

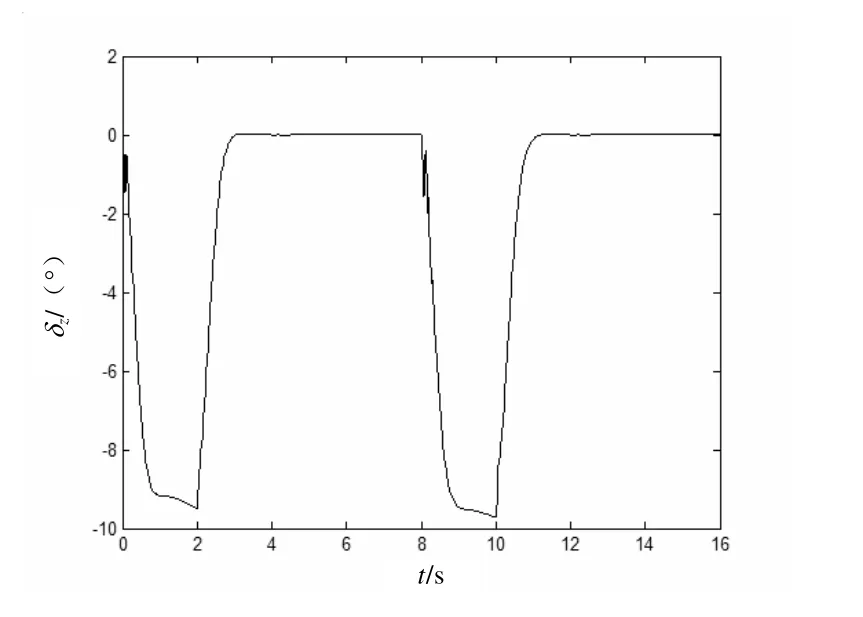
圖4 俯仰舵δz仿真曲線

通過此仿真結(jié)果可知，當俯仰通道模型存在不確定項時，本文提出的控制方法仍然能夠較好地控制 ny、跟蹤 nyc，而且迎角α和俯仰角速度ωz信號都在合理范圍內(nèi)，俯仰舵δz沒有抖振現(xiàn)象。從而，表明應用本文方法設計的俯仰通道控制系統(tǒng)具有良好的動態(tài)品質(zhì)、跟蹤性能和魯棒性。

4 結(jié)論

本文研究了反艦導彈的過載控制系統(tǒng)設計問題，提出了一種自適應模糊滑模控制設計方法。此方法將反演設計、模糊邏輯系統(tǒng)、自適應控制和滑模控制等方法結(jié)合起來，利用模糊邏輯系統(tǒng)估計被控系統(tǒng)的虛擬控制量；利用自適應控制方法估計系統(tǒng)不確定項的未知上界；利用反演設計方法進行系統(tǒng)虛擬控制量和實際控制量的推導。基于有限的已知信息，實現(xiàn)對反艦導彈俯仰通道的過載控制，仿真結(jié)果表明，所設計的俯仰通道控制系統(tǒng)具有良好的動態(tài)品質(zhì)、跟蹤性能和魯棒性。

[1]崔祜濤.基于自適應神經(jīng)網(wǎng)絡非線性飛行控制[J].航空學報,1998,19(2):173-178.

[2]景韶光.非線性神經(jīng)網(wǎng)絡自適應控制及其在導彈中的應用[J].西北工業(yè)大學學報,1997,15(4):603-606.

[3]楊志峰,雷虎民,李慶良,等.基于逆誤差補償?shù)姆蔷€性導彈控制器設計[J].飛行力學,2010,28(4):54-58.

[4]楊志峰,雷虎民,李慶良,等.基于RBF神經(jīng)網(wǎng)絡的導彈魯棒動態(tài)逆控制[J].宇航學報,2010,31(10):2295-2301.

[5]于德海,范作娥,史賢俊.帶落角約束的末端機動Terminal 滑模導引律設計[J].海軍航空工程學院學報,2011,26(5):517-520.

[6]于德海,范作娥,史賢俊.帶落角的反艦導彈自適應模糊滑模三維導引律設計[J].四川兵工學報,2011,32(8):52-55.

[7]錢杏芳,林瑞雄,趙亞男.導彈飛行力學[M].北京:北京理工大學出版社,2000:69-70.

[8]任長娥,佟紹成.基于高增益觀測器的SISO 非線性系統(tǒng)模糊自適應輸出反饋控制[J].遼寧工業(yè)大學學報:自然科學版,2011,31(2):71-80.

[9]郭濤,張軍英.時滯關(guān)聯(lián)大系統(tǒng)的自適應模糊動態(tài)面控制及仿真[J].系統(tǒng)仿真學報,2011,23(2):325-334.

[10]于金鵬,陳兵,于海生,等.基于自適應模糊反步法的永磁同步電機位置跟蹤控制[J].控制與決策,2010,25(10):1547-1551.

[11]文杰,姜長生,薛雅麗.嚴格反饋型非仿射非線性系統(tǒng)的自適應模糊控制[J].控制與決策,2010,25(10):1237-1245.