約束總體最小二乘在空間后方交會中的應用

劉慶元 姜柱

（中南大學地球科學與信息物理學院，湖南長沙410083）

1.引言

空間后方交會是以共線條件方程式為基礎，將像片的6個外方位元素和地面坐標作為待定值看待。首先傳統的方法需要處理大量的三角函數解算，給計算帶來不必要的麻煩，文獻［3］和［4］利用單位四元素法代替三個旋轉角，簡化了計算。但是其平差方法通常采用高斯-馬爾科夫模型進行求解。該模型僅將非線性函數模型在參數概略值處按泰勒級數展開，忽略高次項使其線性化，因此，必然造成系數矩陣中存在誤差。因而，進行平差時必然要考慮到系數矩陣的誤差。為了同時考慮系數矩陣和觀測值的誤差，建立更合理的模型，本文引入了約束總體最小二乘（CTLSE）。該方法可用于解決所謂的變量中的誤差模型的估計問題。

2.單位四元數與共線條件方程式

2.1 單位四元素

四元素是一個四元矢量，可用來描述坐標旋轉。在三維空間中的單位球上的任意一個位置只對應X軸和Y軸旋轉的兩個角，但繞Z軸旋轉的第三個角卻無法描述。這時如果再增加一個自由度就可以表示所有三個旋轉角，這樣便產生了四維空間的單位球。四維空間的單位球定義如下：三維空間中所有三個旋轉角可以通過四維單位球上的點表示，四維單位球上點的四元坐標構成了單位四元數。用單位四元數表示旋轉矩陣為：

由于采用單位四元數對共線條件方程式進行描述，描述像片姿態角時不在出現傳統的角元素，取而代之的是單位四元素的4個系數q0,q1,q2,q3。對共線方程線性化后得出誤差方程式為：

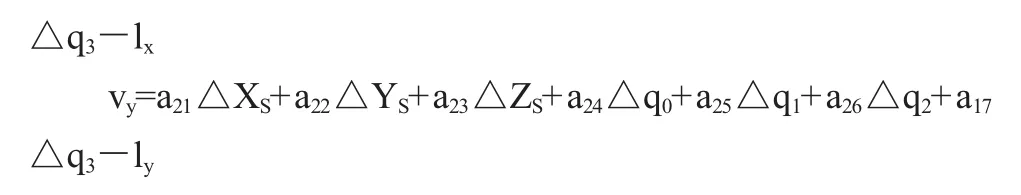
各系數值及常數值見文獻[3]；

結合單位四元數之間的約束條件方程，經線性化后得到：

采用聯系數的直接解法，得到的法方程為：

如此反復趨近，直至每幅影像外方位元素的改正值均小于某個限值時為止，迭代結束。

2.2 約束總體最小二乘（CTLS）

與僅考慮到觀測向量L中是含有誤差的，而認為系數矩陣A中并不存在誤差的最小二乘方法相比，約束總體最小二乘法所關心的是當L和A中都含有誤差，同時考慮這些誤差時，參數向量x的估計方法。令顧及L和A誤差的模型為：

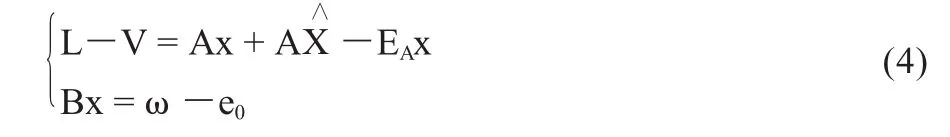
式中，V和EA分別為觀測值和系數矩陣元素的隨機誤差。基于拉格朗日極值的總體最小二乘法，在模型（4）下，總體最小二乘準則可以表示為：

式中，eA=vec(EA)，是將誤差矩陣EA按列拉直得到的列向量，排列順序為從左到右。

由此可得模型（4）在準則（5）下的拉格朗日極值函數為：

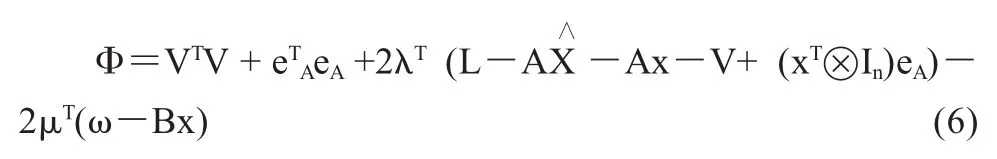
式中，?是表示Kronecker積，EAx=(xT?In)eA

對式（6）求偏導得到拉格朗日條件為：

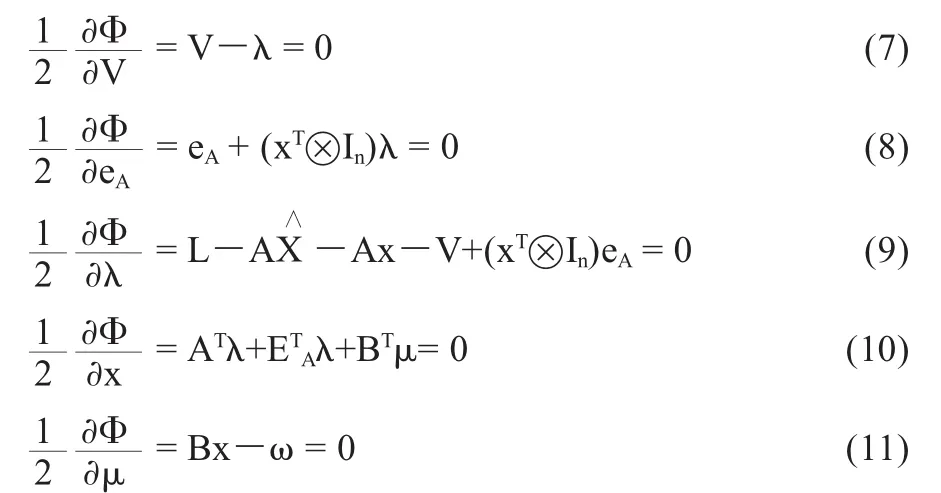
由式(7)和式(9)得

將式（12）代入式（7）和式（8）得，

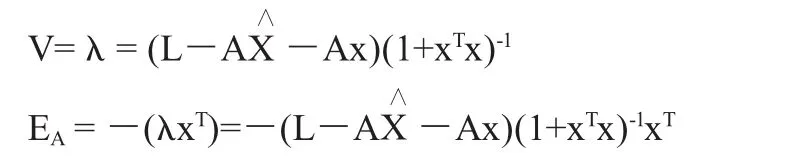
從而得到：

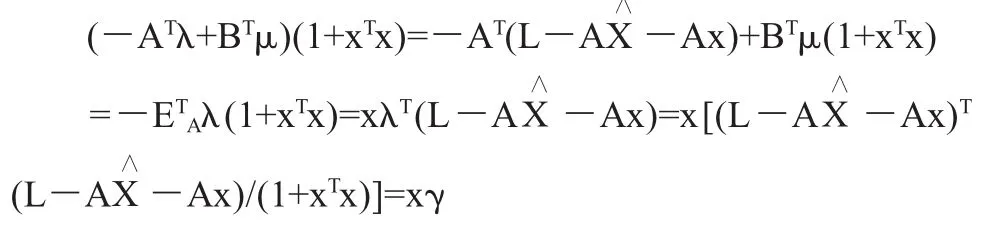
因此，約束總體最小二乘問題的迭代解法為：

第一步：

令γ(0)=0，μ(0)=0；

第二步：

如此反復迭代，直至滿足要求為止。

參數精度為：

3.計算步驟及實例分析

3.1 計算步驟

(1)給定初始值，設K為任意兩點求得的攝影比例尺分母；

(2)代入式（1）和（2）組成誤差方程式；

(3)根據式（13）到（15），直接求得參數的CTLS解，從而求得外方位元素；

(4)利用約束總體最小二乘法對平差結果進行精度評定。

3.2 實例

本文引用文獻[9]中得數據，像片的內方位元素為已知，x0=0，y0=0，f=153.24mm，表1為四個控制點的像片坐標和地面坐標；分別由最小二乘和CTLS方法得到的外方位元素和單位權中誤差以及參數的中誤差見表2。

系數矩陣的殘差矩陣為：EA=10-6

表1 像點坐標和控制點坐標

表2 兩種平差方法的比較

4.結論

(1)采用單位四元素描述的平差模型與傳統方法相比，單位四元素利用四個獨立的量代替三個旋轉角度，在實際計算時避免了頻繁的三角函數運算，簡化了運算過程，提高了效率。

(2)約束總體最小二乘（CTLS）不僅考慮了觀測值L所含有的誤差，同時也考慮了系數矩陣A所含有的誤差，數學模型與實際情況更加吻合，同時求得到的單位權中誤差和參數的中誤差都要比傳統的最小二乘計算的結果小，得到的計算結果精度更高。

[1] 張廣軍.視覺測量[M].科學出版，2008.

[2] 王之卓.攝影測量原理[M].武漢大學出版社，2007.

[3] 王勇，姜挺，江武剛等.基于單位四元素描述的單像空間后方交會[J].測繪科學技術學報，2007，24(2).

[4] 曾卓喬.一種不測定初始值的近景攝影測量微機程序[J].測繪學報，1990(4).

[5] Burkhard Schaffrin，Andreas Wieser On weighted total least-squares adjustment for linear regression 2008，(82)：415-421.

[6] 陳瑋嫻，袁慶，陳義.約束總體最小二乘在點云數據拼接中的應用[J].大地測量與地球動力學，2011，31(2).

[7] 王娟，陳安平.總體最小二乘問題解算的兩種方法比較分析[J].測繪信息與工程，2010，(6).

[8] 陸鈺，陳義，鄭波.總體最小二乘方法在三維坐標轉換中的應用[J].大地測量與地球動力學，2008，28(5).

[9] 陳義，陸鈺，鄭波.總體最小二乘方法在空間后方交會中的應用[J].武漢大學學報信息科學版，2008，33(12).

[10] 彭天強，張文林，常寧.高精度參數估計問題[J].數學的實踐與認識，2007，37(14).