動態數據驅動的航班延誤預測研究＊

陳海燕 王建東 徐 濤

（南京航空航天大學計算機科學與技術學院1） 南京 210016）

（中國民航大學計算機科學與技術學院2） 天津 300300）

近10a來，國內外學者針對航班延誤原因、傳播模型［1］及如何減少延誤［2］等問題進行了研究.目前，常用的航班延誤預測方法一般采用確定性模型，勢必會忽略一些重要的隨機因素，如突發事件.因此，對航班延誤實時預測毫無意義.

航班延誤實時預測本質上是一個動態系統狀態估計問題.本文將仿真領域最新研究成果——動態數據驅動應用系統（dynamic data driven application system，DDDAS）范型用于航班延誤的實時預測，對連續進港航班延誤波及問題進行分析和建模，基于系統狀態空間模型構建了一種動態數據驅動的航班延誤預測框架，并用某樞紐機場的歷史航班運行數據驗證該方法的有效性.

1 DDDAS應用問題

傳統的系統仿真方法是將早期測量得到的靜態數據輸入到系統模型中預測現在或未來系統的變化.然而，由于早期測量數據并不能及時和準確的反映動態系統的實時變化情況，仿真的結果往往與實際測量結果相差甚遠，導致預測失敗.為此，美國國家科學基金會于2000年提出全新的仿真預測分析系統——DDDAS［3］，旨在將仿真和實驗有機結合起來，使仿真可以在執行過程中動態地從實際系統接收數據并做出響應，而仿真結果可以動態地控制實際系統的運行，指導測量的進行.

目前，DDDAS在交通運輸領域的已有一些應用成果.Fujimoto等［4］基于一種微觀城市地面交通仿真模型，根據所采集到的實時交通流數據來優化信號控制、確定當前地面交通狀態及預測未來狀態.Huang［5］重點研究了在軌道交通中如何在仿真過程中不斷利用實測數據對預測模型進行校驗以獲得更精確可靠的預測輸出.Wang［6］提出了一種基于隨機宏觀高速公路交通流模型和擴展卡爾曼濾波技術的實時高速公路交通狀態估計器.在空中交通領域，Hyatt［7］給出了一種航班延誤預測DDDAS框架和實時數據采集方法.

從上述研究中可以總結出，要應用動態數據驅動方法進行系統狀態預測必須解決2個關鍵問題：（1）預測模型.根據系統行為特征建立一個可計算的預測模型，能反映系統狀態之間的關系，及系統狀態與可測數據之間的關系；（2）數據同化.根據模型性質確定一種數據同化算法，能將動態實測數據融合到模型預測中，達到更新預測結果的目的.

2 航班延誤狀態空間模型

2.1 延誤問題分析

由于同一時間跑道只能供一架飛機使用，連續進港的相鄰兩航班之間的存在延誤波及問題.在計劃緊湊的情況下，若前行航班發生延誤，會引起鏈式反應，將延誤影響傳播到后行航班.設飛機在發出準備降落就緒信號前產生的延誤為已知的累積延誤，在發出準備降落就緒信號后產生的延誤為降落延誤，兩者之和為該航班的進港延誤.設進港延誤為d，降落延誤為l，累積延誤為a，波及延誤為p，前后行飛機之間存在最小飛機間隔時間為m，兩飛機間緩沖時間為b，m包含在b中，且必須得到滿足.前行飛機對后行飛機的延誤波及產生過程見圖1.

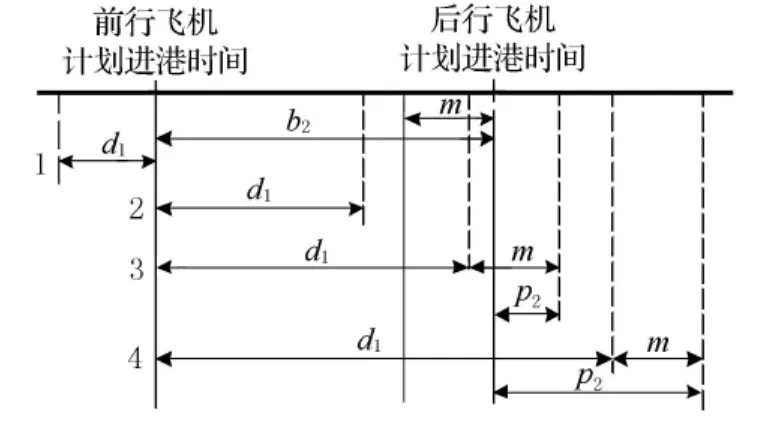
圖1 延誤波及產生過程

可見，當d1大于b2和m之差時，為確保最小飛機間隔，后行飛機將產生波及延誤p2，后行飛機的降落延誤可表示為

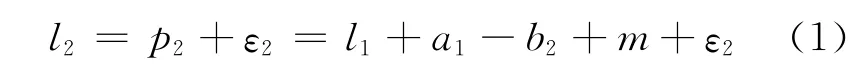
式中：ε2為降落過程中由其他隨機因素引起的延誤.

2.2 狀態空間模型

通過上節對航班降落延誤問題的分析，可將系統狀態空間模型表示為如下分段線性模型：

其中：式（2）為過程方程；式（3）為觀測方程；xk為第k個航班的降落延誤；ak為第k個航班的累積延誤；bk為第k個航班的計劃間隔；m為最小飛機間隔，按規定執行；yk為觀測值；wk，vk為過程噪聲和觀測噪聲；εk為隨機延誤.由于影響航班降落的因素較復雜，且各種因素與航班延誤之間的關系很難用數學模型表示，因此，εk不能直接計算得到.這里可采用智能數據挖掘算法，從歷史數據中學習到隨機因素的影響模式，估計出當前情況下的εk；若遇極端情況，如空中管制、惡劣天氣等，可直接參考專家意見.關于εk的計算已由另文發表［8］，本文不再展開討論.

3 動態數據驅動的航班延誤預測

3.1 動態數據驅動的航班延誤預測系統框架

基于狀態空間模型構造出動態數據驅動的航班延誤預測框架見圖2.

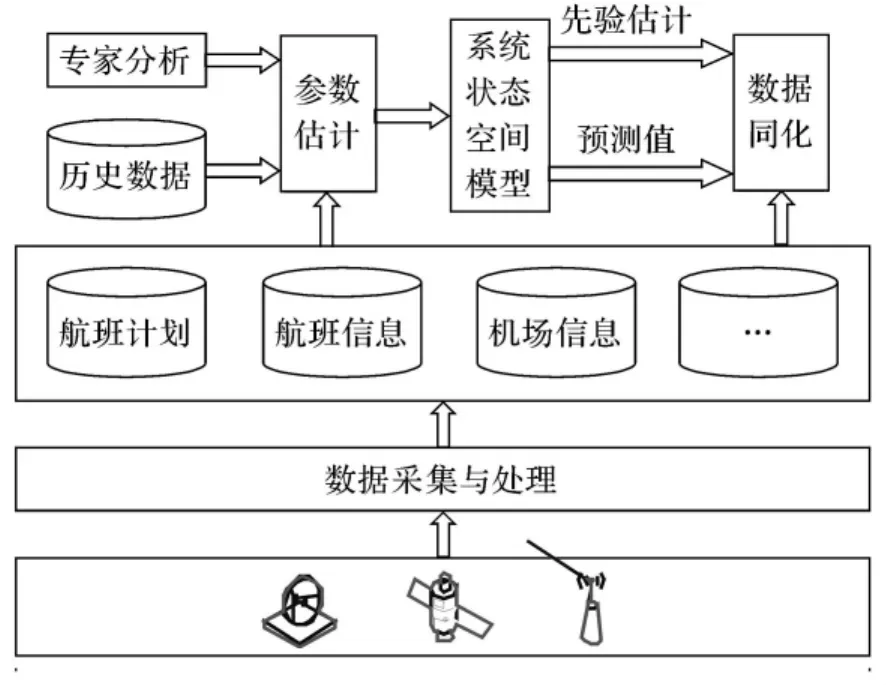
圖2 動態數據驅動的航班延誤預測框架

該框架由4個主要模塊組成：（1）數據采集與處理模塊.完成實時數據的采集和處理，為參數估計和數據同化提供輸入數據；（2）參數估計模塊.根據實時數據估計狀態空間模型中ak，bk，wk，vk，εk等參數在當前條件下的取值；（3）系統狀態空間模型.根據過程方程所描述的前后行航班降落延誤之間的關系，計算出后行航班降落延誤的先驗估計值作為數據同化的輸入；（4）數據同化模塊.用實際測量的結果來更新或優化模型預測的結果，目前可用卡爾曼濾波［9］或粒子濾波［10］方法實現數據同化，前者適用于線形系統狀態估計，后者適用于非線性非高斯系統的狀態估計.

3.2 基于卡爾曼濾波的狀態預測

1）初始化狀態初值x0及其協方差P0.

2）時間更新 根據xk－1，Pk－1計算xk和Pk的先驗估計

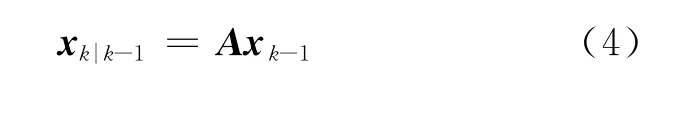
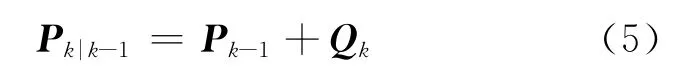
式中：Qk＝Var（wk）.

3）測量更新 當新的觀測值yk到達時，更新xk｜k－1，Pk｜k－1，得到xk和Pk的后驗估計

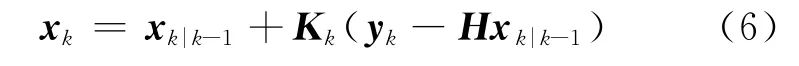
式中：K為卡爾曼增益，計算方法為

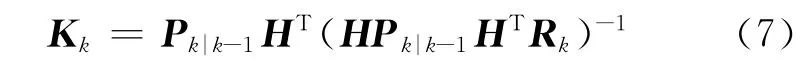
式中：Rk＝Var（vk）.

4）重復2），3）預測不斷向前推進.

4 實驗及結果分析

本文在Matlab平臺上進行了一系列實驗，實驗數據來源于國內某樞紐機場航班運行歷史記錄.實驗從不同角度展開，在驗證動態數據驅動航班延誤預測能力的同時，還驗證了噪聲、連續預測步數等因素對預測準確度的影響.

實驗1 考察動態數據驅動航班延誤預測的準確度，以及噪聲方差R，Q取不同值時對預測結果的影響.圖3顯示了對50架連續進港航班進行降落延誤預測的結果.

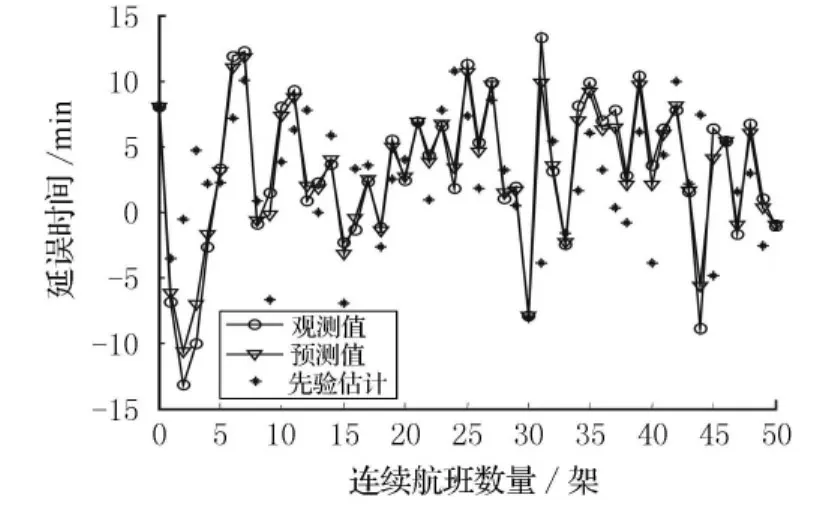
圖3 預測結果

5組不同的經驗（R，Q）值下，先驗估計、預測值（后驗估計）與實際觀測值之間最終的均方根誤差見表1.

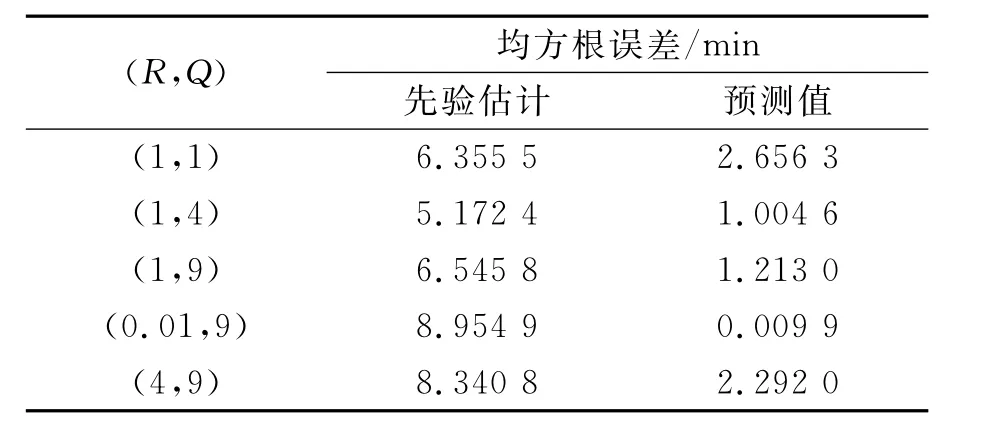
表1 不同（R，Q）值下的均方根誤差

由表1可見，融合實時觀測數據能明顯提高預測的準確度；（R，Q）取值對預測準確度有重大影響.

實驗2 考察預測不同數量連續航班時預測準確度的變化，均方根誤差見表2.

表2 均方根誤差隨連續航班數量的變化

從表2可以看出：連續航班數量對預測準確度的影響不大，動態數據驅動的延誤預測方法有較好的穩定性.

5 結束語

本文提出了一種動態數據驅動的航班延誤預測方法.該方法能在利用系統狀態空間模型進行先驗預測的同時，將采集到的有關航班運行過程的各種實時數據反饋到預測過程中，用于動態地更新延誤預測值.實例研究證明所提出的動態數據驅動的航班延誤預測方法具有較高的預測準確度，且受被測連續航班數量的影響很小.這就為機場或航空公司預測未來航班的執行、制定減少航班延誤的相關決策及進一步的機場環境預測提供了有力支持.

［1］Abdelghany K F，Shah S S，Raina S，et al.A model for projecting flight delays during irregular operation conditions［J］.Journal of Air Transport Management，2004，10（6）：385－394.

［2］AhmadBeygi S，Cohn A，Lapp M.Decreasing airline delay propagation by re－allocating scheduled slack［J］.IIE Transactions，2010，42（7）：478－489.

［3］Darema F.Dynamic data driven application systems［R］.NSF Workshop on Dynamic Data Driven Application Systems，March，2000.

［4］Hunter M，Fujimoto R，Suh W，et al.An investigation of real－time dynamic data driven transportation simulation［C］∥Proceedings of the 2006Winter Simulation Conference.Washington，DC，USA：IEEE，2006：1 414－1 421.

［5］Huang Y，Seck M D，Verbraeck A.Towards automated model calibration and validation in rail transit simulation［C］∥Procedia Computer Science1，2010：1 259－1 265.

［6］Wang Y，Papageorgiou M，Messmer A，et al.An adaptive freeway traffic state estimator［J］.Automatica，2009（45）：10－24.

［7］Hyatt R，Bansal D，Chakraborty S，et al.Flight cast－an airline flight delay predicting DDDAS［C］∥Proceedings of 2007International Symposium on Distributed Computing and Application to Business，En－gineering and Science.Wuhan China，Hubei Science and Technology Press，2007：85－88.

［8］Chen H Y，Wang J D，Xu T.Modeling of flight delay state－space model based on genetic EM algorithm［J］.Transactions of Nanjing University of Aeronautics ＆ Astronautics，2011，28（3）：276－281.

［9］Kalman R E，Bucy R.New results in linear filtering and prediction problems［J］.Journal of Basic Engineering，1961，83（1）：95－108.

［10］B?lviken E，Acklam P J，Christophersen N，et al.Monte carlo filters for non－linear state estimation［J］.Automatica，2001，37（2）：177－183.