聲在隨機介質波導中的傳播

楊士莪

(哈爾濱工程大學 水聲工程學院，黑龍江 哈爾濱 150001)

迄今為止，對于聲在隨機介質中傳播起伏問題的研究，絕大部分僅限于無限介質的環境條件，很少有人討論波導傳播所可能附加的效應.而且除Rytov方法以外，所利用的數學工具，如Feynman所提出的路徑積分等方法，多數工程技術人員也都很不熟悉［1-3］.為此，采用逐次近似方法討論在波導條件下，聲傳播起伏的某些特點，將是有實際參考意義的.為了數學上的簡便，文中將僅限于討論點源聲波在具有絕對軟上邊界，和半無限流體介質下邊界的平面平行波導中的傳播，且波導和下半空間中的介質總體均勻，其平均聲速和密度分別為:c0、ρ0、c1、 ρ1，但上、下方介質中均具有隨機的微弱不均勻起伏，這樣將仍能反映出介質起伏對聲信號傳播的主要影響規律.

1 聲場基本方程式

取直角坐標，令波導深度為H，聲源位于z軸上深度為zs處，這時波導中及下方介質中聲場勢函數φ(0)(r)、φ(1)(r)應滿足的微分方程式可分別寫為

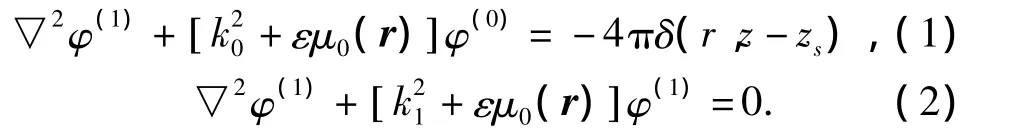
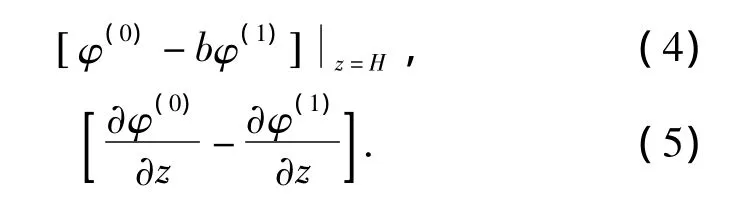
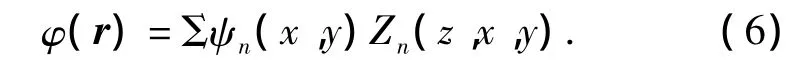
式中，Zn(z，x，y)為第n階局地簡正波，并應滿足下列方程式與邊界條件:

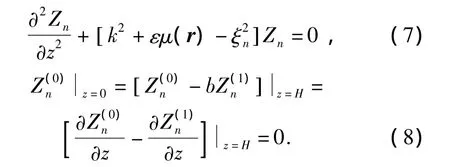
將Zn寫為ε的冪級數，即

將此表示代入式(4)，按照ε的同冪次項進行整理后，可分別得到:

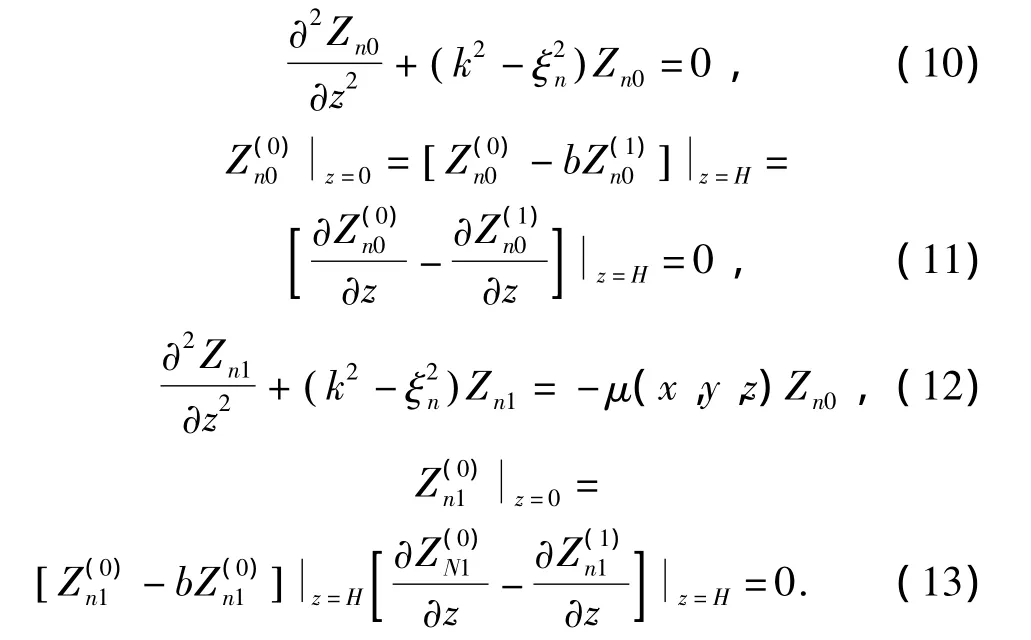
上述公式及今后為了書寫簡便起見，對φ、ψ、Z等函數，當其有關公式基本相同時，即省略各函數的肩標，而不再分別列出.已知對兩層均勻介質的Pekeris波導有:

根據式(12)、(13)求解聲場的一次近似時，可選用以下函數做為微分方程的2個線性獨立解:

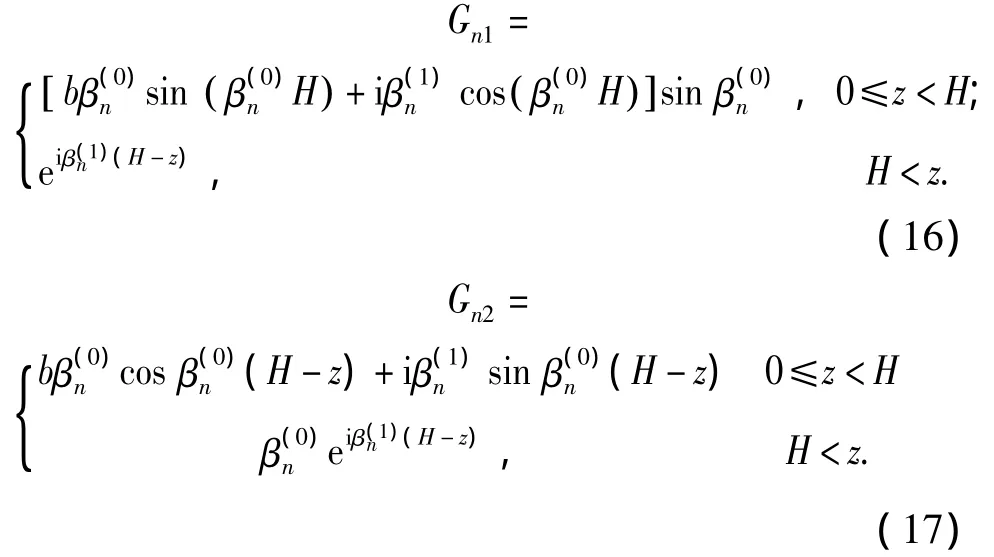
依照二階微分方程求特解的方法，最后可得

其中:

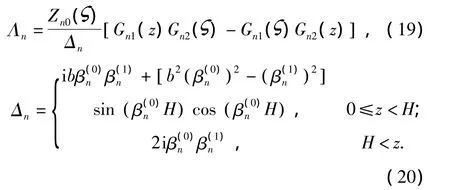
Λn、Δn均為與隨機量無關的確定性函數.由于原所選取的G1、G2均滿足邊界條件(11)，故可知上式給出的Zn1的解，也必然滿足給定的邊界條件.按照以上方法，可依次求得更高階的近似，可以看出，Zn的各高階近似，將相應的含有μ(x，y，x)的高冪次項.為簡便，在此將僅考慮Zn的一階近似.

2 信號起伏的時空相關函數

首先計算各ψn的近似值.根據耦合簡正波方法，利用各階簡正波的正交性，忽略局地簡正波空間變化的二階小量，可得:

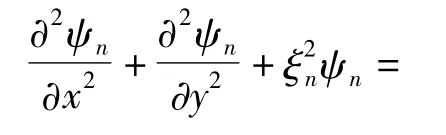
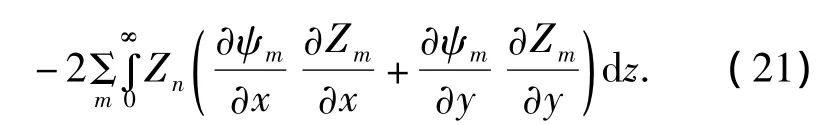
對于不存在隨機不均勻體的兩層液態介質波導來說，作為0階近似有其中并滿足上式右端為0的微分方程式.注意到，故上式等號右邊的項可視為當波導中存在隨機不均勻體時，引發聲場水平勢函數分量修正值的二次聲源.同樣將ψn展開寫成ε的冪級數:

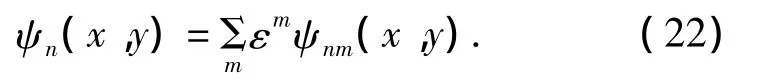
若僅考慮一階近似，可得:

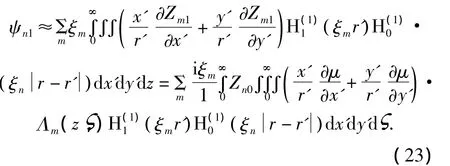
若需要計算ψn的更高階近似，可依前述利用逐次近似法進行.當僅考慮一階近似時，可得到波導中信號起伏值為

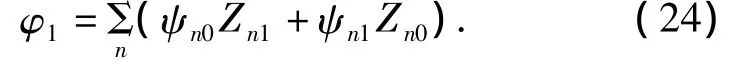
從上式中可以看出，由于波導中存在隨機起伏的不均勻體，不僅各階局地簡正波有變化，且各階勢函數水平分量也有變化.需要注意的是:這時ψn與Zn均不是μ(x，y，z)的線性函數，因此即μ(x，y，z)服從0均值的Gauss分布規律，波導中信號起伏一般也不遵從Gauss規律，僅在一級近似條件下，可以近似的認為服從Gauss規律.

利用式(15)計算信號起伏的水平和垂直相關函數時，考慮到各不同階簡正波相互干涉，其空間平均值近似為0，因而可以僅計算相同階簡正波的結果;同時還可以考慮到，聲場勢函數水平分量的起伏，和介質起伏的空間梯度有關，而簡正波的起伏則與介質起伏直接相關，因而可認為ψn1與Zn1相互獨立，其統計平均值也可以忽略.從而得到如下公式:

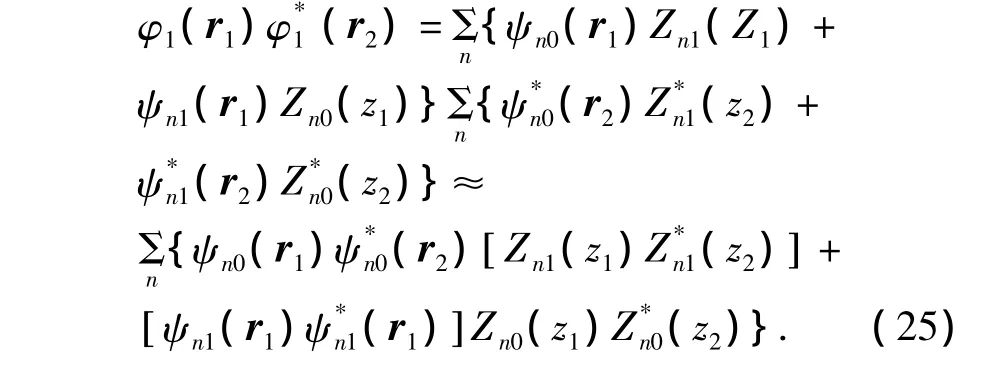
設介質起伏的空間相關函數為

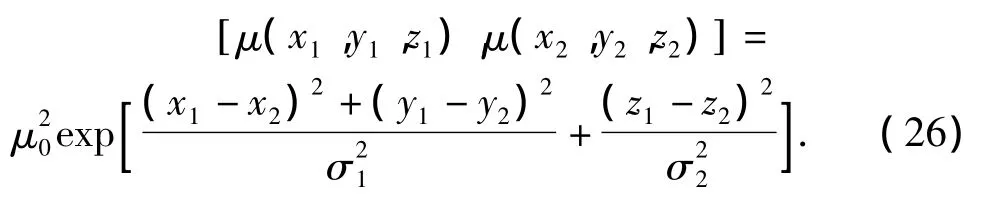
經過若干計算后可得:

1)波導中信號起伏的均方值:

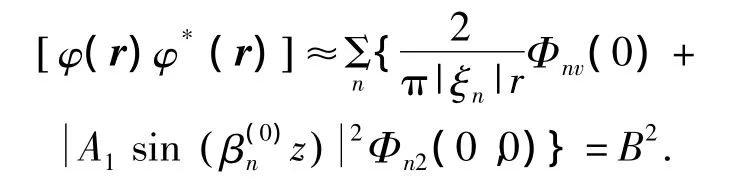
2)波導中信號起伏的垂向相關系數:

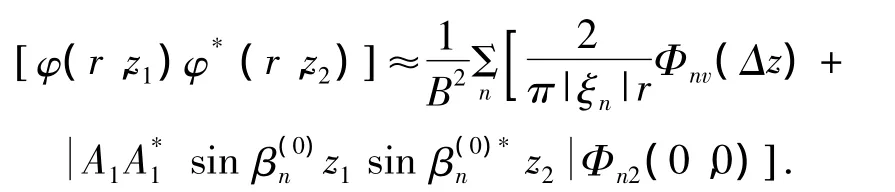
3)波導中信號起伏的縱向相關系數:

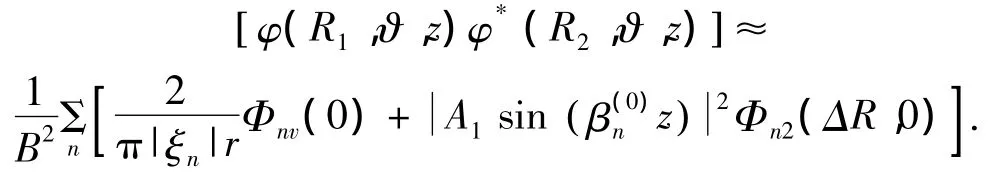
4)波導中信號起伏的橫向相關系數:

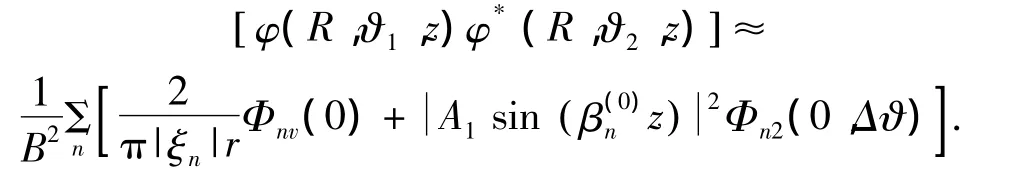
其中:

從上述各表達式可以看出，無論是波導中信號起伏的均方值，抑或是信號起伏的各項空間相關函數，都將和接收點與聲源的相對位置有關.由于具體公式的復雜性，很難直接從解析公式中看出應有的規律，而需要利用數值計算進行分析討論.由于篇幅的限制，具體的仿真計算結果，以及試驗驗證情況，將在后續文章中給出.

3 結論

文中介紹了一種利用逐次近似法，分析當介質環境存在微小擾動時，聲在波導中遠距離傳播情況下的起伏方法.從有關計算過程中可以看出，由于波導中存在隨機起伏的不均勻體，在聲波傳播過程中，不僅各階局地簡正波有變化，且各階勢函數水平分量也有變化.需要注意的是:這時ψn與Zn均不是μ(x，y，z)的線性函數，因此即或μ(x，y，z)服從0均值的Gauss分布規律，波導中信號起伏一般也不遵從Gauss規律，僅在介質起伏率甚小的一級近似條件下，可以近似的認為服從Gauss規律.隨著傳播距離的竲加，高階簡正波逐漸衰減，信號起伏的空間相關將會逐漸竲大，但具體的規律十分復雜，將在后繼工作中借助數值分析進行討論.

［1］YANG Shie.Theory of underwater sound propagation［M］.哈爾濱:哈爾濱工程大學出版社，2009.

［2］FLATTE S M.Sound transmission through a fluctuating ocean［M］.Cambridge:Cambridge University Press，1979.

［3］Ярощук И О，Гулин О Э.Метод статистичекого моделирования в зачах гидроакутики.Владивосток Дальнаука，2002.

［4］BERTSATOS I.General second-order covariance of Gaussian maximum likelihood estimates applied to passive source localization in fluctuating waveguides［J］.The Journal of Acoustical Society of America.2010，128(5):2635-2651.