改進SVC算法在雷達信號分選中的應用
趙貴喜,穆成新,劉永波,王睿東
(解放軍93163部隊,哈爾濱 150001)
0 引 言
隨著現代科學技術的不斷發展,各種體制雷達不斷涌現,使得雷達信號環境日益復雜,這就對雷達信號分選提出了新的要求。傳統的基于利用脈沖重復間隔(PRI)單參數進行信號分選的方法已經越來越不能適應當前復雜的電磁環境。支持向量聚類(SVC)是由Asa Ben.Hur等人在支持向量機的基礎上提出的一種非參數聚類算法,被廣泛應用于各個領域。
本文將SVC聚類算法應用到雷達信號分選中,在利用SVC進行聚類分析時發現,SVC不僅時間復雜度高,而且在處理分布復雜、不均勻的樣本時,識別率較低。K-Means聚類算法在處理大量數據時時間復雜度不高,但是存在需要事先確定數據聚類數目的明顯缺陷,本文將SVC聚類算法與K-Means聚類算法相結合,提出了聯合聚類分選算法,并通過仿真實驗驗證了算法的可行性。
1 SVC算法
SVC聚類是2001年由Asa Ben-Hur等人在支持向量機的基礎上提出一種非參數聚類算法。它的基本思想是:將樣本點經過一個非線性映射映射到一個高維特征空間,并在此空間中尋找一個包圍所有樣本點且具有最小半徑的超球,當這個球面被映射到數據空間時,能分割成幾個部分,每個部分都包含了獨立的數據點聚類,位于球表面的點即為支持向量,一個高維空間的球在原來的空間中可以是任意的形狀。
SVC通過二次規劃問題求解,得到全域最優解,而且能處理任意形狀的聚類,并劃分有重疊區域的聚類形狀,對噪聲也能有效分析[1-3]。
定義1:設數據空間x i∈Rd,數據集{x i}∈X,包含d維空間i個數據點,運用非線性變換將數據從x映射到高維特征空間,尋找Hilbert空間最小包絡x點的超球體半徑R。為了發現帶有軟邊界的最小包絡球體,表達為:
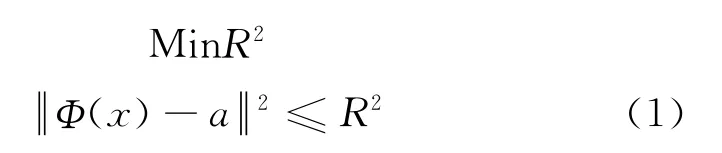
式中:||·||為歐基里德函數;a為球體中心。
引入松弛系數ξj,式(1)變為:
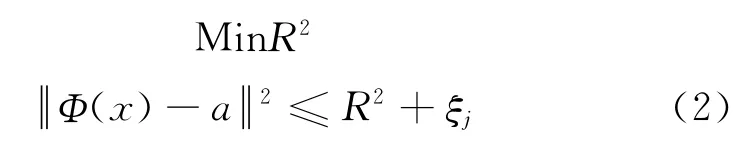
引入拉格朗日乘式:

如果βi=C,則表示點x i映象位于特征空間的球體之外,被稱作約束支持向量(SV)。如果0<βj<C,則點x i的映像將位于特征空間球體的表面。這樣的點被當作是支持向量(SV)。SV位于聚類邊界,基本支持向量(BSV)位于邊界之外,其他所有點都在邊界之內。
用高斯核函數K(x i,x j)表示點積,則得到只包含βj的Wolfe對形式為:
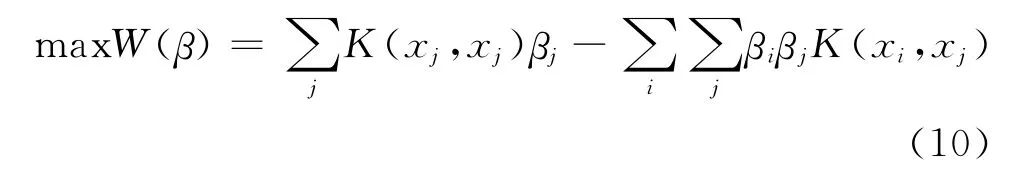

SVC算法在處理中等規模的數據樣本時,計算和存儲非常困難,而且對于分布復雜、不均勻的樣本,尋找獲得全局最優聚類配置的參數值極其困難,容易陷入局部最優解,而非全局最優[4-5]。
2 KSVC聯合聚類算法
2.1 K-Means聚類算法
K-Means聚類算法由 Mac Queen首先提出,屬于聚類方法中一種基于劃分的方法,它是一種較簡單的迭代優化方法。該算法首先隨機地選擇k個對象,每個對象初始地代表了一個類的平均值或中心。對剩余的每個對象,根據其與各個類的中心距離,將它賦給最近的類,然后重新計算每個類的平均值。這個過程不斷重復,直到準則函數收斂。通常采用平方誤差準則。
K-Means聚類算法選用雷達數據的脈沖到達角(DOA)tDOA、載頻(RF)fRF和脈寬(PW)τPW三維參數作為聚類分選參數。設某一信號p i經過標準化處理后,取出tDOA、fRF和τPW這三維數據,成為新的形式p′i(tDOA,fRF,τPW),i=1,2,…,N,這樣就形成了雷達脈沖描述向量集合P′= {p′1,p′2,…,p′N}。K-Means聚類就是要找到P′的一個劃分V k={C1,C2,…,C k},使目標函數f(V k)值收斂最小。f(V k)為:
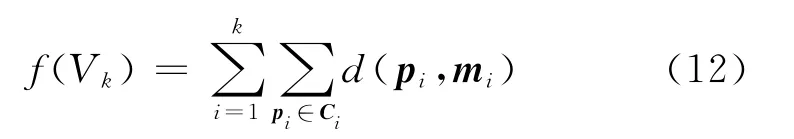
從K-Means聚類算法分選流程上可以看出,有2個關鍵步驟可以影響聚類結果:
高等動物細胞核直徑一般為5~10 μm,高等植物細胞核直徑一般為5~20 μm。教師利用超輕黏土、廢棄膠頭滴管膠帽和細鐵絲等材料,分別模擬核模、核孔復合體和核酸,制作放大約4萬倍的細胞核模型(即直徑約20 cm),如圖1所示。
(1)聚類數目k在算法開始運行之前必須確定,然而這個k值的選定往往是困難的。很多時候,并不知道給定的全脈沖數據應該分成多少部雷達才最合適。如果聚類數目k設置不正確,聚類分選會出現嚴重的“增批”和“漏批”現象。在實際運用中,k值要么直接給定,要么根據經驗來選取,沒有一個比較通用的好方法。這是該算法的局限性。
(2)初始聚類中心的選擇。這是K-Means算法的關鍵步驟,這種隨機選擇初始聚類中心的方式常常使算法在不同的運行中產生不同的聚類結果,很多時候有可能得不到最佳的聚類結果,算法常以局部最優結束,甚至出現無解。
2.2 聯合分選算法
K-Means聚類算法當選定合適的初始聚類中心和合適的聚類數目時會取得良好的分選效果,而SVC聚類分選算法是一種無監督聚類分選算法,不需要事先知道數據的類別數目。
基于以上考慮,本文將2種聚類算法相結合,利用SVC算法事先確定雷達信號數據的分類數目,再利用K-Means分選算法進行分選,從而縮短聚類分選時間和復雜程度。
算法描述如圖1所示。
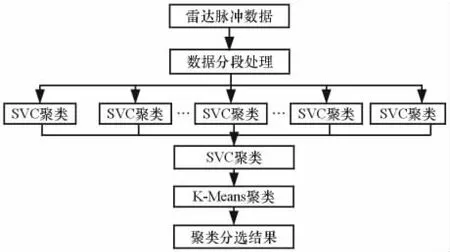
圖1 算法描述圖
聯合聚類算法采用雷達脈沖到達角tDOA、脈沖重頻fRF和脈沖寬度τPW3個參數聯合分選,按如下步驟執行:
(1)讀入雷達脈沖數據,提取雷達信號參數tDOA、fRF和τPW進行數據標準化處理;
(3)對每段數據分別進行SVC聚類處理;
(4)將分段聚類的數據再進行SVC聚類處理,得到數據的初始劃分;
(5)運用聚類算法提供的初始聚類數目和初始聚類中心作為輸入,用K-Means算法進行聚類分析;
(6)統計聚類信息,輸出結果。
3 仿真實驗
實驗模擬了4部雷達,按照到達時間進行混合,對同時到達的信號進行丟失處理,共320個脈沖信號。雷達參數設置如表1所示。
4部雷達混合數據經過標準化后,分布如圖2所示(圖中“*”代表雷達脈沖)。
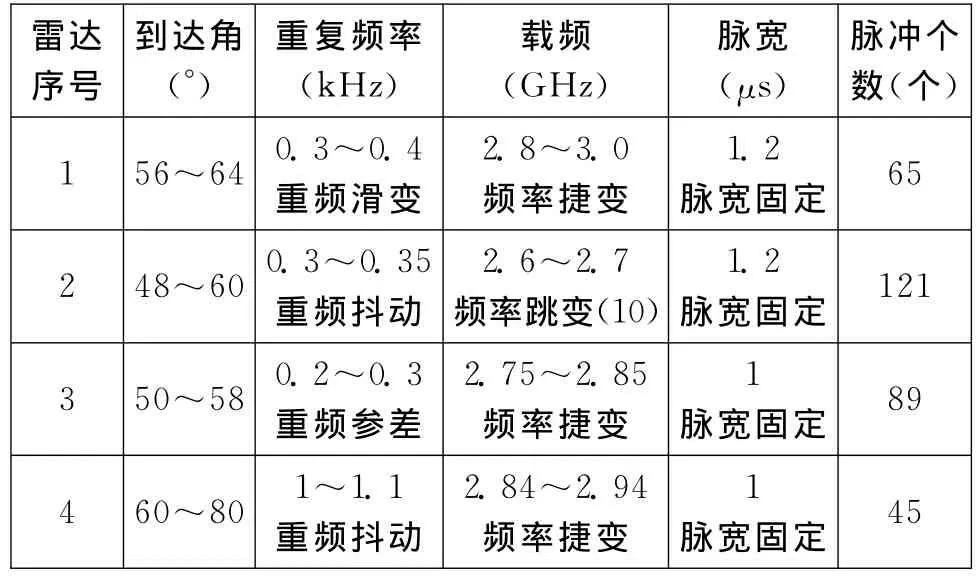
表1 雷達仿真數據
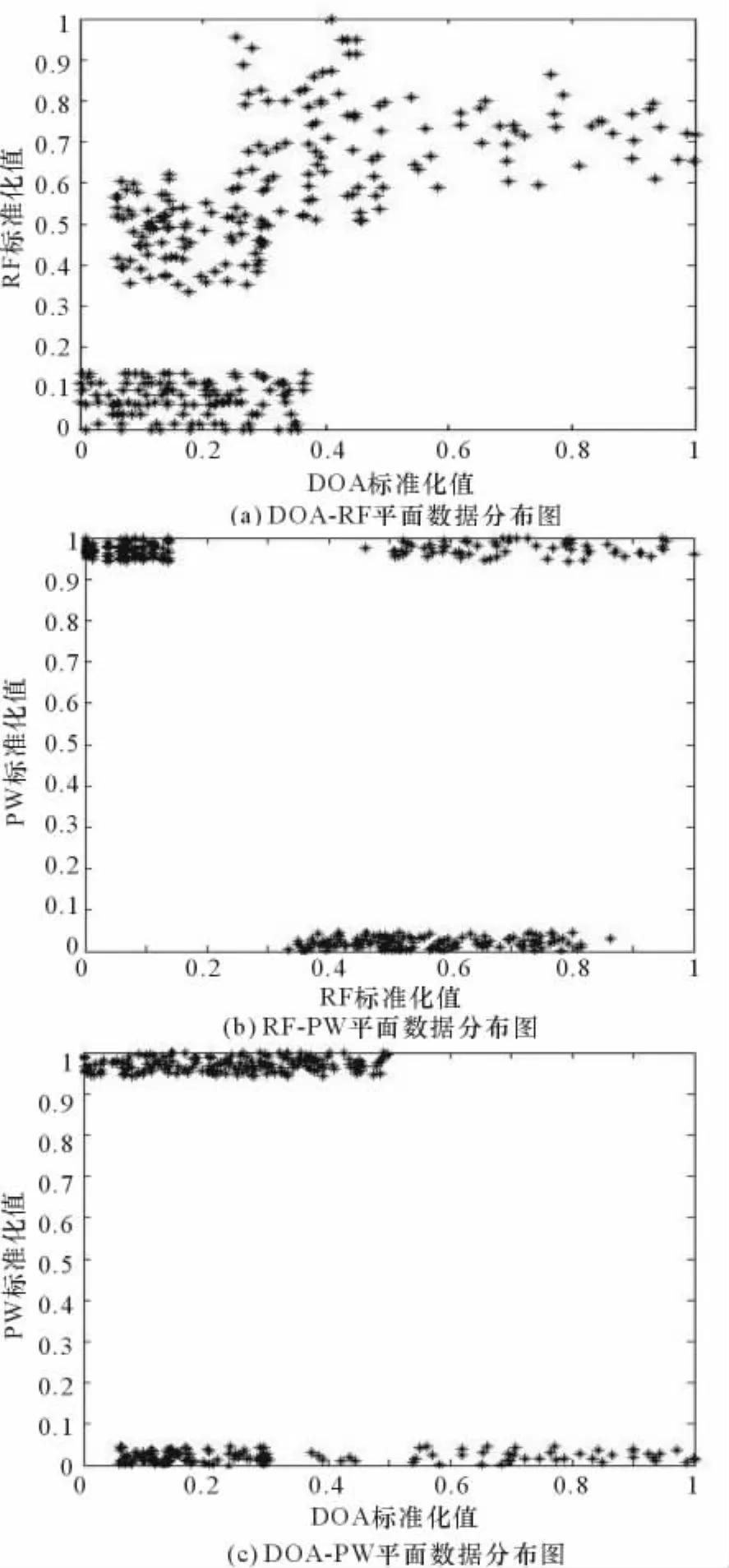
圖2 雷達混和數據二維屬性分布圖
從圖2(a)、2(b)、2(c)的雷達混合數據分布圖可以看出,4部雷達在不同的屬性維度上混合嚴重,從圖3(d)的分選結果可以看出本文提出的聯合聚類分選算法準確地將混合數據分選成了4類,并且每部雷達數的分選數目正確。
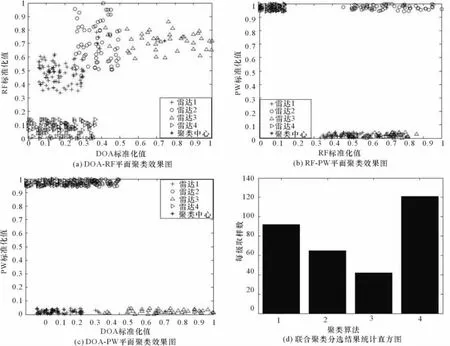
圖3 聯合聚類分選效果圖
通過詳細的對比可以看出雷達A中有5個數據被錯誤地分選成了雷達B,雷達B中的5個數據被錯誤地分選成了雷達A,雷達C和雷達D均正確分選,分選正確率達到96.88%。
4 結束語
本文提出的基于SVC聚類和K-Means聚類的聯合聚類分選算法可以很好地分選出雷達信號,經過仿真實驗驗證取得了比較理想的效果。這只是本文對雷達信號分選算法的一種嘗試,還存在很多缺點,如處理大量數據時,消耗時間較長,參數設置困難,這些都有待進一步研究。
[1]蘇意玲.一種基于支持向量機和聚類的Web挖掘新方法[J].計算與現代化,2009,172(12):33-35.
[2]蔣加伏,趙嘉,胡益紅.一種基于支持向量聚類的圖像分割 方 法 [J].計 算 機 工程 與 應 用,2009,45(30):165-167.
[3]孫德山,李海清.基于線性規劃的支持向量聚類算法[J].計算機工程與設計,2010,31(6):1305-1307.
[4]Francesco Camastra,Alessandro Verro.A novel kernel method for clustering[J].IEEE Transaction on Pattern Analysis and Machine Intelligence,2005,27(5):801-805.
[5]孫德山,吳今培.基于線性規劃的多類支持向量機算法[J].計算機科學,2005,32(10):160-163.

