MIMO雷達測向性能研究與分析

田增彬，方 標，杜溢智，袁湘輝

（1.海軍裝備部，北京 100641；2.海軍工程大學，武漢 430033）

0 引 言

考慮到地物、障礙等環境因素對目標不同部分散射信號的反射，雷達接收的信號是各多徑信號的疊加，具有與通信中角度擴展相似的特性。此外，雷達目標具有明顯的閃爍特性，理論和實驗均表明，雷達目標在姿態和方向上的微小變化都將導致雷達回波的嚴重起伏，可達10～25 d B［1］。這種回波信號的起伏十分類似于移動信道的信號衰落，將嚴重影響常規雷達的探測性能。鑒于雷達回波信號具有某些與移動通信信道相似的特性，將已在移動通信中得到深入研究的多輸入多輸出（MIMO）概念，延伸應用于解決雷達信號接收和目標探測問題，是近年來雷達研究的一種可行的嶄新嘗試。

MIMO技術是指在發射端和接收端分別使用多個發射天線和接收天線，信號通過發射端和接收端的多個天線發送和接收，以改善每個用戶得到的服務質量。其核心是空時信號處理，也就是利用在空間中分布的多個天線將時間域和空間域結合起來進行信號處理，有效地利用了隨機衰落和可能存在的多徑傳播成倍地提高業務傳輸速率。

在MIMO技術的基礎上，針對傳統雷達體制探測存在的不足，美國學者最先提出了MIMO雷達的概念。該體制雷達采用了空間分集（角度分集）與信號分集技術，整個雷達系統可從不同方向對目標進行探測，利用了目標的起伏來改善雷達的性能，較好地克服了目標RCS的角閃爍所帶來的性能損失，獲得了較大的空間分集增益，從而在信號檢測能力上較傳統雷達有其獨到特點。國際上比較知名的MIMO雷達研究技術方向主要有美國麻省理工學院MIT的林肯實驗室提出的發射分集方案和貝爾實驗室提出的收發全分集的技術方案［2］。

本文主要討論MIMO雷達工作于測向（DF）模式時可能達到的最佳性能。在雷達DF系統中，接收機對目標的方位估計是基于目標的反射回波的。為了簡化模型，這里作如下假設：

（1）發射信號矢量是復合正態分布的隨機變量，存在空間白噪聲，并且具有相關矩陣為（1／M）I M的固定功率譜密度；

（2）發射和接收天線陣元都是全向的；

（3）接收信號的獨立快拍是可處理的。

1 MIMO雷達測向基本原理

在用于測向的MIMO雷達中，發射天線的間隔需滿足對關注目標正交的重要條件，同時接收陣列的單元間隔足夠小，以便能進行DF測量［3］。假定目標相對于接收陣列法線的角度為θ0，接收矩陣為K＝I Q?aT（θ0）。為了照射目標以實現空間分集，發射機上的相移被設置為0°，可得出通道矩陣為：

調節目標矢量α后，接收矢量r為復合的、具有相關矩陣（2M）－1‖α‖2a（θ0）a＋（θ′0）＋R S／N－1I N的多變量范數，θ′0為發射陣列方位角。

為了更好理解，研究M＝2，N＝1的特殊情況。該信號模型為：

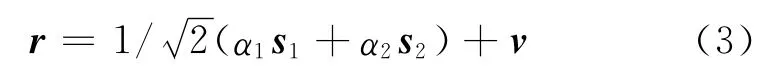
如果2個天線發射相同的波形，即s1＝s2＝s，那么接收信號模型為：

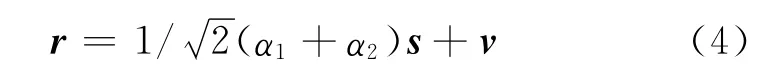
由于通道參數a1，2在接收機處是未知的，故不可能利用目標多樣性搜索。

因為當Q→∞時，隨機變量具有χ2分布，而且它們是獨立同分布的（利用g1和g2之間的正交性），所以式（5）中的目標分量具有χ24分布。這是因不同發射天線單元的目標引起了不同和不相關RCS的結果。因此，MIMO雷達最后得到了分集增益。

2 仿真設計與結果分析

2.1 仿真原理

均方誤差（MSE）可以用于比較不同系統的性能，系統的MSE取決于具體使用的算法，如最大似然估計、MUSIC算法、波束形成等。本文通過比較無偏估計器的最低邊界——克勞美羅界來評價不同系統的性能。

2.1.1 克勞美羅界（CRB）

在 MIMO測向雷達中，接收信號模型［4，5］為：

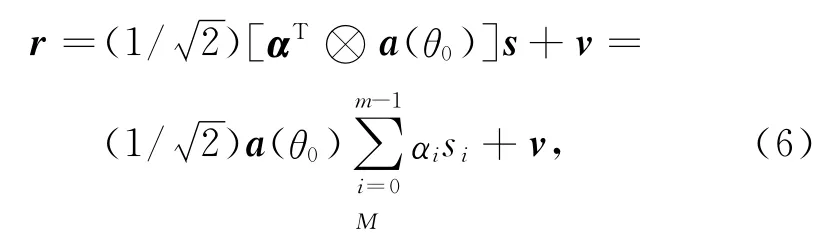
調節通道參量a，令為1個零均值、方差為（1／M）‖α‖2的復合正態隨機變量。

在這個模型中有3個未知的參量：方位參量θ，目標參量α以及信噪比R S／N，令矢量ψ＝ ［θ，R S／N，‖α‖2］以表示各個未知的參量。克勞美羅界（CRB）是無偏估計器的MSE所能達到的最小值，用p（r｜ψ）表示接收信號參數的分布，則關于ψ的CRB可表示為：

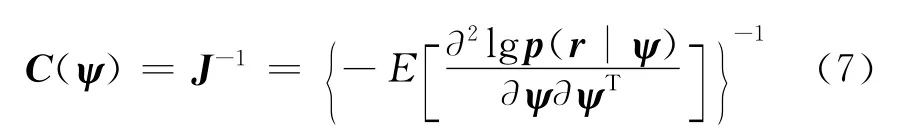
由于關心的是目標方位θ，所以其它參量對于估計反而成了干擾，通過調節α，可使r為具有相關矩陣 （2M）－1‖α‖2a（θ）aH（θ）＋R S／N－1I N的復合正態分布的隨機變量。則CRB可表示為：

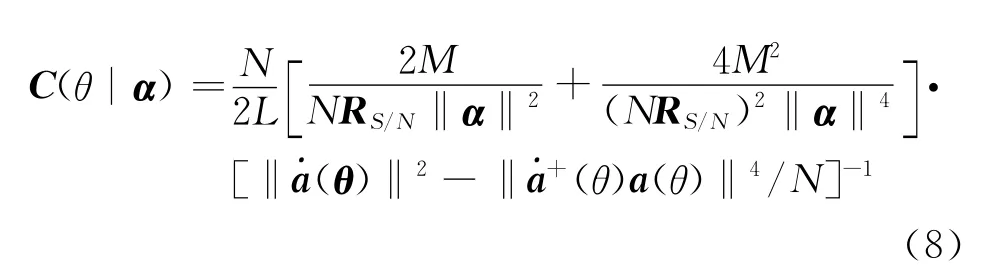
式中：L為陣列估計方位所使用的快拍數。

通過求CRB關于α的均值，可以得到：

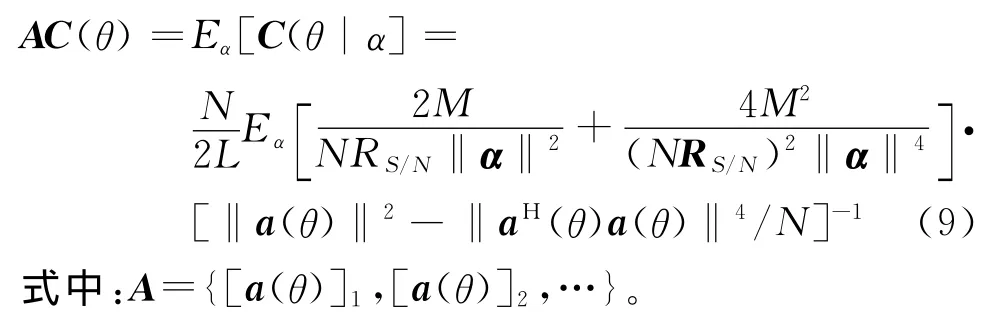
2.1.2 均勻線列陣

使用全向接收天線的均勻線列陣，假設有N個接收陣元，陣元間隔為半波長，則第n個陣元的控制向量等效為［5］：

最后，基于式（14）建模、編寫 MATLAB程序，進行仿真［6］。

2.2 仿真結果

2.2.1 不同發射陣元數下的性能分析

本節討論的是發射天線陣元個數對系統性能的影響，假設均勻線性陣列（ULA）接收陣元數N＝6，來波方位α′＝30°，快拍數L＝80，在發射陣元數改變的情況下，獨立進行10次實驗，分別求出不同陣元數條件下角度的均方根誤差，如圖1所示。

從圖1可以看出，對于MIMO測向雷達，發射天線的陣元數目增加時，系統性能有一定的改善，但對于系統估計的誤差影響幅度不是很大。圖1所求出的各條曲線基本重合，證實了這一點，即系統對于發射天線陣元數的不敏感性。并且，通過增加發射天線陣元來提高系統性能存在1個下界，即當M的值達到一定程度時，估計誤差幾乎不再改變。另外，信噪比（SNR）的增大對性能的改善有很明顯的作用，但當SNR較大時，它的改善作用不再明顯。

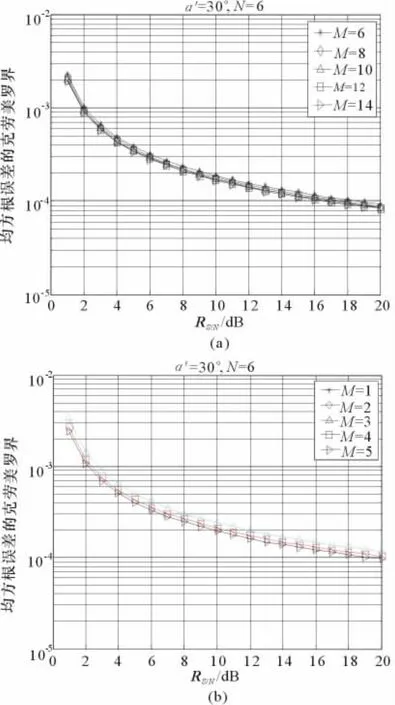
圖1 不同發射陣元數下的克勞美羅界

2.2.2 不同接收陣元數下的性能分析

假設ULA發射陣元數M＝6，來波方位α′＝30°，快拍數L＝80，在接收陣元數改變的情況下，獨立進行10次實驗，分別求出不同陣元數條件下角度的均方根誤差，如圖2所示。

從圖2中可以看出，隨著接收天線陣元數目的增加，估計誤差隨之有較大的改善，但是降低的幅度逐漸減小。同樣，信噪比（SNR）的增大對性能的改善也有很明顯的作用，但當SNR較大時，它的改善作用不再明顯。

在分別討論了發射陣元和接收陣元數目變化對DF性能的影響之后，接下來對發射陣元和接收陣元數目同時變化時的影響進行仿真。假設來波方位α′＝30°，快拍數L＝80，在發射陣元數和接收陣元數同時改變的情況下，獨立進行10次實驗，分別求出不同陣元數條件下角度的均方根誤差，如圖3所示。

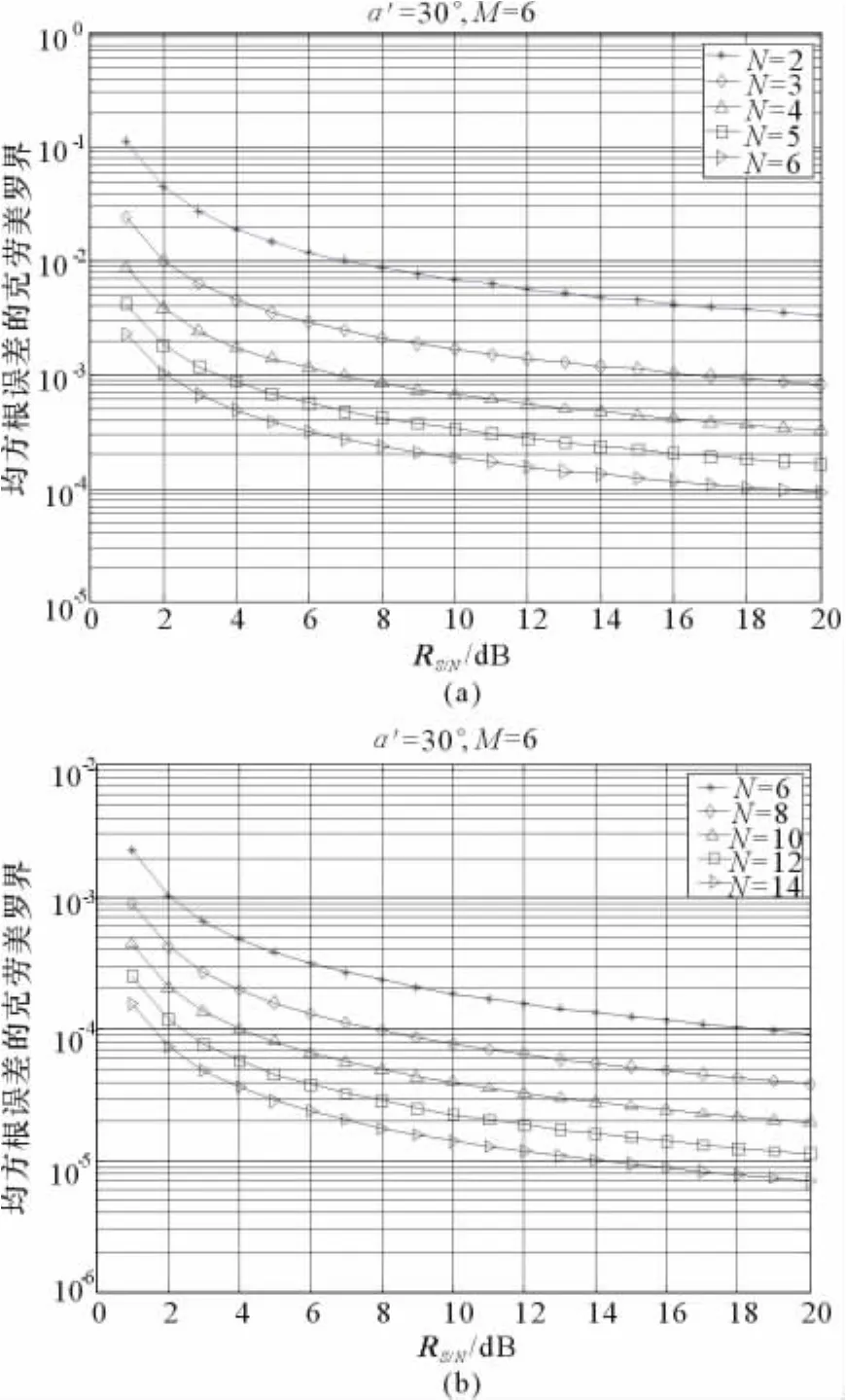
圖2 不同接收陣元數下的克勞美羅界

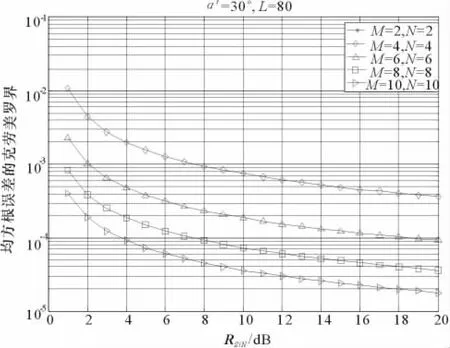
圖3 不同發射陣元和接收陣元數下的克勞美羅界

將圖3和圖1、圖2進行比較可以看出，同時增加發射天線陣元和接收陣元數量，可以更加快速地提高MIMO雷達的方位估計性能，當然，也可以看到其在相同陣元數目下改善的幅度是同等的。

2.2.3 不同快拍數下的系統性能分析

假設1：ULA接收陣元數N＝6，來波方位α′＝30°，在快拍數改變為240的情況下，改變發射陣元數目，獨立進行5次實驗，分別求出不同陣元數條件下角度的均方根誤差，如圖4所示。

圖4 固定快拍數和接收陣元數下的克勞美羅界

假設2：ULA發射陣元數M＝6，來波方位α′＝30°，在快拍數改變為240的情況下，改變接收陣元數目，獨立進行5次實驗，分別求出不同陣元數條件下角度的均方根誤差，如圖5所示。

將圖4、圖5與圖1、圖2比較，可以看出對于發射天線陣元或接收天線陣元數目的變化，當提高快拍數L時，估計精度都相應地變高。為了更加直觀地比較L對系統的影響，再做出如下假設：ULA發射陣元數M＝6，接收陣元數N＝6，來波方位α′＝30°，在快拍數改變的情況下，獨立進行5次實驗，分別求出不同快拍數條件下角度的均方根誤差，如圖6所示。

通過圖6可看出，在發射陣元和接收陣元不變以及來波方向不變的情況下，通過改變快拍數L可以很大程度地改善系統性能，只是當L值很大時，改善的幅度逐漸減小。但是采用這種方法的代價是系統復雜度的增加，因此通常根據實際情況取1個適當的值。

3 結束語

本文對MIMO雷達測向性能進行了仿真分析，驗證了基于MIMO體制雷達的優勢，通過不同發射天線陣元數、接收天線陣元數以及不同快拍數條件下系統方位估計MSE的克勞美羅界，計算分析了采用MIMO技術帶來的雷達測向性能的改善。MIMO雷達作為一個新生事物，盡管目前國際上仍處于概念研究階段，但它是一種很有發展潛力的新型雷達，值得繼續關注和研究。相信在不久的將來，MIMO雷達一定會得到快速的發展。

［1］黃韜，袁超偉，楊睿哲.MIMO相關技術與應用［M］.北京：機械工業出版社，2007.

［2］Fishler E，Haimovich A，Blum R.MIMO Radar：an idea whose time has come［A］.Radar Conference of Proc.IEEE［C］，2004：71－78.

［3］強勇，張冠杰，李斌.MIMO雷達及其應用研究［J］.火控雷達技術，2010，39（1）：1－10.

［4］明文華，劉志學.一種新體制雷達——MIMO雷達［J］.火控雷達技術，2008，37（1）：10－13.

［5］Skolnik M.Radar Handbook［M］.Third Edition.Newyork：McGraw－Hill，2008.

［6］Liew T H，Hanzo L.Space－time codes and concatenated channel codes for wireless communications［J］.Proc.IEEE，2002，90（2）：187－219.

［7］Zhu X，Murch R D.Performance analysis of maximum likelihood detection in a MIMO antenna system［J］.IEEE Transactions on Communications，2002，50（2）：187－191.