葉片外換熱計算程序STAN5收斂性改進
婁德倉
(中國燃氣渦輪研究院,四川 成都 610500)
1 引言
渦輪葉片燃氣邊的換熱系數,可通過數值求解流過型面的粘性流控制微分方程得到。這種解法的優點是:可得到壁面附近氣流的速度和溫度分布,且在此基礎上求得的壁面摩阻系數和換熱系數較為準確;能較方便地應用近年來發展的湍流模型;計算中用到的經驗公式少,適應性較廣。由于求解邊界層方程的計算量較求解N-S方程的小得多,因而在工程計算中得到了較廣泛的應用。Crawford等人于1975年采用Patankar-Spalding方法編制了邊界層微分方程計算程序STAN5[1],隨后又對該程序進行了諸多改進。目前使用的TAXSTAN程序是其最新版本[2],能考慮葉片表面氣膜出流對外換熱的影響。
上世紀80年代,STAN5程序被西工大劉松齡教授等引入國內,經改進后用于渦輪葉片外換熱計算,結合氣膜修正等經驗公式,能用于帶氣膜冷卻渦輪葉片的熱分析。鄧化愚等人[3]還對程序進行了改進,主要是加入了湍流度間隙因子,使程序能考慮來流湍流度對外換熱的影響。蔡毅等人[4]通過微分法、積分法等的對比,發現STAN5程序在計算方法及精度上更具優勢。但在應用STAN5程序進行外換熱計算時,會出現不收斂等問題,這主要是由外邊界的逆壓梯度分布、計算網格及邊界層卷吸量的控制等因素引起。因此,計算中經常要對渦輪氣動數據進行人工干預,這會造成計算結果的人為誤差。為此,本文對STAN5程序計算中存在的收斂性等問題進行分析,并采取相應措施進行改進。
2 邊界層微分方程
描述軸對稱可壓縮流的邊界層流動方程,包括連續性方程、動量方程和能量方程。其中連續性方程可表示為[5]:

式中:坐標x、y的方向分別與物體的型線相切和垂直,u和v分別為x、y方向的分速度,ρ為氣流密度,r為徑向坐標。
動量方程為:

式中:p為壓力,μ為動力粘性系數,ρ----u′v′為湍流剪切應力,u′和v′分別為x、y方向的湍流脈動速度,z為單位質量流體上的徹體力。
總焓形式的能量方程為:

式中:I為氣體總焓,λ為氣體導熱系數,cp為氣體定壓比熱,i為氣體靜焓;I′為總焓脈動值,S為單位質量流體中的源項。
根據以上方程,用已知的邊界條件和初始條件,便可解出ρ、u、v、I在邊界層內的分布。對于湍流邊界層,還須補充求湍流剪切力的關系式。
3 STAN5程序求解
3.1 初始條件
求解邊界層微分方程過程中,常將駐點區域層流邊界層作為計算初始條件。在STAN5程序中,根據Pohlhausen公式獲得層流邊界層內的速度分布:

式中:δ為邊界層厚度,Λ為Pohlhausen參數,ue為邊界層外氣流速度。
邊界層起始點溫度分布(T)可通過溫度分布與速度分布間的線性關系得到,關系式為:

式中:Tw為壁面溫度,Te為邊界層外氣流溫度。
3.2 湍流模型
現有的STAN5程序中采用的湍流模型有混合長度模型、單方程湍流模型,同時考慮了湍流度修正。其中較為常用的是Prandtl混合長度模型。
3.3 邊界層網格變換
邊界層微分方程求解方法很多,STAN5程序采用的是Patankar和Spalding提出的流函數坐標變換法[6],首先從x、y坐標變換為x、ω(x,y)坐標,對邊界層微分方程進行求解,然后再將結果返回到x、y坐標下。ω(x,y)及其與y的關系可用下式表示:
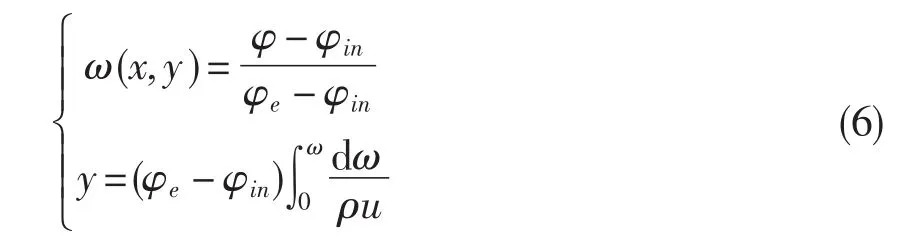
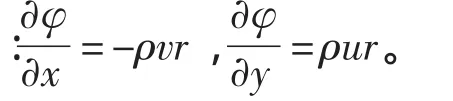
STAN5程序中的網格,其徑向分布采用基于式(7)建立的速度分布與網格密度關系。為保證邊界層底層網格有足夠的密度,采用了滑移點控制方法。

式中:c1為常數,β為滑移點參數。
4 STAN5在計算中存在的主要問題及改進
以某渦輪葉片外換熱計算過程為例。STAN5程序在計算葉片外部換熱時,首先將葉片表面的等熵馬赫數分布作為邊界層計算中的外部速度邊界。通過求解邊界層微分方程,獲得葉片表面換熱系數分布。典型的渦輪葉片表面等熵馬赫數分布如圖1所示。從圖中看,在渦輪葉片葉盆側前緣擴張段和尾緣激波區存在明顯的逆壓梯度,而這些位置通常會造成外換熱計算不收斂。因此在外換熱計算過程中,通常要對外部勢流速度進行人為調整,避免出現逆壓梯度(如圖1中虛框內所示)。由于邊界層微分方程為橢圓型微分方程(即下游計算結果完全受上游的影響),因此該調整會導致計算結果人為誤差較大,影響外換熱計算結果的精確性。

圖1 渦輪葉片表面等熵馬赫數分布Fig.1 Isentropic Mach number distribution of blade surface
4.1 收斂性問題及分析
根據邊界層內部流動方程的量級分析,邊界層內部的壓力分布可簡化為式(8)。其中沿流向的壓力梯度決定于外部主流的速度分布。因此,在外部勢流存在較強逆壓梯度且邊界層底部速度較小時,計算中就會出現速度負值。而邊界層網格又與速度分布相關,最終導致計算發散。

通常,邊界層內部出現速度負值時,STAN5程序自身會對速度負值進行調整(如式(9)),同時減少邊界層外部的卷吸流量,重新求解方程。

如圖2所示,修正后的速度分布與邊界層內真實的速度分布有很大差別。若繼續計算,仍會出現速度負值,導致計算發散。有時雖能得到收斂結果,但所采用的方法已改變了邊界層外部的氣流速度分布規律(圖3),并且這種收斂方式會對換熱系數(α)產生較大影響(圖4)。
4.2 收斂性的兩點改進
通常在邊界層方程計算中,若出現速度負值,表明邊界層已破壞,這時邊界層方程不再適用。程序自身的修正實質上是假設該區域內仍然為邊界層型流動。在渦輪流道中,大部分區域屬于順壓梯度的邊界層流動,因此該局部區域內采用此假設仍然合理。本文在此基礎上對逆壓梯度下的速度分布u(y)及其網格密度進行修正。



4.2.1 逆壓梯度下的速度分布
針對葉片外部速度場急速變化時產生的較強逆壓梯度,可采取兩種方法進行速度修正。
一是在當前計算站速度梯度出現負值時,對速度分布進行修正,如圖5(a)所示。當前計算點xi的速度分布形式ui(y),與前一計算點xi-1的速度分布形式ui-1(y)保持相似,即:

圖5 邊界層內部速度分布修正Fig.5 Modification of the velocity profile inside the boundary layer

結果表明該方法不能完全避免速度負值問題。
二是在當前計算站存在逆壓梯度且速度二次梯度出現負值時,對速度分布進行修正,如圖5(b)所示。當前計算點xi的速度分布形式ui(y),與前一計算點xi-1的速度分布形式ui-1(y)保持相似,并保持外邊界的速度值uei不變,即:

結果表明該方法能明顯改善計算不收斂。
4.2.2 基于壓力梯度變化的自適應網格
葉盆側尾緣激波區馬赫數變化劇烈,壓力梯度迅速由順壓梯度變為逆壓梯度,因此該區域對流向網格變化較敏感。雖采取了上述速度分布修正,但在有些馬赫數分布下仍會出現計算不收斂。通常邊界層在尾緣區域較厚,沿流向的空間步長較大(Δx=0.3δ),這時會出現兩種情況:一是當前節點位于最大(或較大)逆壓梯度點,導致計算發散;二是當前節點跨過最大(或較大)逆壓梯度點,計算穩定收斂。
為使邊界層內部沿流向網格步長與主流壓力梯度相聯系,在逆壓梯度下,采用式(12)計算網格步長:

式中:下標old表示上一步長的參數,Δx0為當前計算站下的初始步長,Δx1為經壓力梯度修正后的計算步長。圖6對比了壓力梯度修正前后葉片尾緣附近的網格,可見修正后的網格明顯變密。
經上述修正,STAN5程序計算中的不收斂現象得到解決。修正過程中,保持外邊界速度不變,就能保證計算結果誤差在合理范圍內。

圖6 修正前后的沿流向網格Fig.6 Comparison of the stream-wise mesh before and after modification
5 計算結果分析

圖7 外換熱計算結果分布Fig.7 External heat transfer coefficient of the blade
根據圖1中的馬赫數分布,改進后的STAN5程序外換熱計算結果與人工修正馬赫數分布計算結果間的對比如圖7所示。從圖中看出,兩者間的外換熱分布趨勢一致,但在葉盆側,兩者的計算值相差約±4%,最大達20%。采用新型網格的計算結果中,對尾緣激波區域(如圖中葉背尾緣)的換熱系數分布更加詳細。圖8為邊界層內部的速度分布云圖。

圖8 邊界層內部的速度分布云圖Fig.8 Contour of velocity inside the boundary layer
6 結論
本文分析了渦輪葉片外換熱計算程序STAN5中的求解方法,包括邊界層求解的微分方程、計算初始條件及網格變換等。針對程序在外流場存在較強逆壓梯度時所出現的計算不收斂及錯誤收斂等現象,對該程序進行了兩點改進:修正了逆壓梯度下邊界層內部速度分布,建立了邊界層內部沿流向的網格分布與主流壓力梯度間的聯系。改進后的程序有效地避免了計算發散等問題。算例分析結果表明,本文提出的改進方法與以前的人工調整方式獲得的結果相比,外換熱系數分布趨勢一致,局部誤差約為4%,最大誤差達20%。
[1]Crawford M E,Kays W M.STAN5-A Program for Numeri?cal Computation of Two-Dimensional Internal and Exter?nal Boundary Layer Flows[R].NASA CR-2742,1976.
[2]Kays W M,Crawford M E,Weigand B.Convective Heat and Mass Transfer[M].4thed.McGraw-Hill,2005.
[3]鄧化愚,蔡 毅,劉玉芳.渦輪氣冷葉片局部外換熱系數計算方法的改進[J].燃氣渦輪試驗與研究,1989,2(2):1—5.
[4]蔡 毅,劉松齡.渦輪葉片外換熱系數計算方法和比較[J].燃氣渦輪試驗與研究,1995,8(1):1—8.
[5]航空發動機手冊總編委會.航空發動機手冊:第16冊——空氣系統及傳熱分析[K].北京:航空工業出版社,2001.
[6]Patankar S V,Spalding D B.Heat and Mass Transfer in Boundary Layers:A General calculation Procedure[M].London:International Textbook Company Ltd.,1970.

