二維海面上方金屬目標(biāo)復(fù)合散射快速算法研究

姬偉杰 童創(chuàng)明，2

(1.空軍工程大學(xué)導(dǎo)彈學(xué)院，陜西 三原 713800；2.毫米波國(guó)家重點(diǎn)實(shí)驗(yàn)室，江蘇 南京 210096)

引 言

目標(biāo)與隨機(jī)地海面的復(fù)合電磁散射研究在軍用和民用領(lǐng)域都有廣泛的應(yīng)用，引起了國(guó)內(nèi)外學(xué)者的極大關(guān)注，但是大多數(shù)研究都側(cè)重于二維散射問(wèn)題[1-6]。對(duì)于在實(shí)際中遇到的三維散射問(wèn)題研究則比較少，而且大多采取解析法來(lái)求解以降低計(jì)算復(fù)雜度[6-7]。解析法對(duì)于粗糙面參數(shù)有嚴(yán)格的適用范圍，不能用于計(jì)算復(fù)雜參數(shù)粗糙面與目標(biāo)的復(fù)合散射，同時(shí)不能得到交叉極化的結(jié)果。數(shù)值算法不受此限制，因此，研究求解實(shí)際地海面與目標(biāo)復(fù)合散射的快速數(shù)值算法具有重要意義。

在二維粗糙面與目標(biāo)的復(fù)合散射計(jì)算中，不僅要考慮目標(biāo)與粗糙面自身的散射，還要考慮它們之間的相互作用，而其中粗糙面的未知量占絕大多數(shù)。因此，如何快速有效地計(jì)算粗糙面的電磁散射是一個(gè)重要的問(wèn)題。以往的方法都是將目標(biāo)與地海面當(dāng)作整體來(lái)建模以及求解[8-11]，由于數(shù)值算法都要產(chǎn)生矩陣方程，這就導(dǎo)致矩陣數(shù)據(jù)量過(guò)大而不能快速求解。N.Dechamps 等提出了一種計(jì)算一維分層粗糙面的快速數(shù)值算法：層內(nèi)波傳播展開(kāi)法[12](PILE)，將通過(guò)矩量法(MoM)得到的線性方程組求解分成四步來(lái)迭代求解：兩步用來(lái)求解單層粗糙面自身的散射；兩步用來(lái)求解上層粗糙面與下層粗糙面之間的相互作用。Kubicke G等進(jìn)一步將其擴(kuò)展應(yīng)用于計(jì)算粗糙海面上方金屬目標(biāo)的復(fù)合電磁散射特性[13]。

推導(dǎo)了二維粗糙面上方目標(biāo)復(fù)合散射的耦合積分方程組，將PILE算法擴(kuò)展應(yīng)用于求解該積分方程組。PILE的優(yōu)點(diǎn)就是將目標(biāo)與粗糙面的散射分開(kāi)來(lái)考慮，因此，粗糙面的表面積分方程可以用已經(jīng)成熟的快速數(shù)值算法來(lái)求解，如稀疏矩陣平面迭代及規(guī)范網(wǎng)格法(SMFSIA/CAG)[14]，它所需內(nèi)存小、計(jì)算速度快，是一種計(jì)算二維導(dǎo)體粗糙面電磁散射的有效快速數(shù)值算法。而目標(biāo)的未知量較小，其表面積分方程可以采用傳統(tǒng)的基于三角屋頂(RWG)基函數(shù)的MoM來(lái)求解[15]。

利用該算法計(jì)算了具有PM海浪譜的海洋粗糙面上方各種典型目標(biāo)的復(fù)合雙站散射系數(shù)，通過(guò)與傳統(tǒng)MoM的結(jié)果相比較，驗(yàn)證了算法的有效性，討論了算法的收斂性。計(jì)算了海面上導(dǎo)彈目標(biāo)的雙站散射系數(shù)(BSC)。該算法提供了一種計(jì)算二維粗糙面上方目標(biāo)復(fù)合電磁散射的有效途徑。

1.基礎(chǔ)理論

1.1 耦合積分方程組

圖1所示為二維隨機(jī)海洋粗糙面上方金屬目標(biāo)的散射，ki與ks分別為入射與散射方向矢量，θi與φi為入射角，θs與φs為散射角，H為目標(biāo)距離海面高度，粗糙面的高度函數(shù)z=ζ(x，y)，且〈ζ(x，y)〉=0.

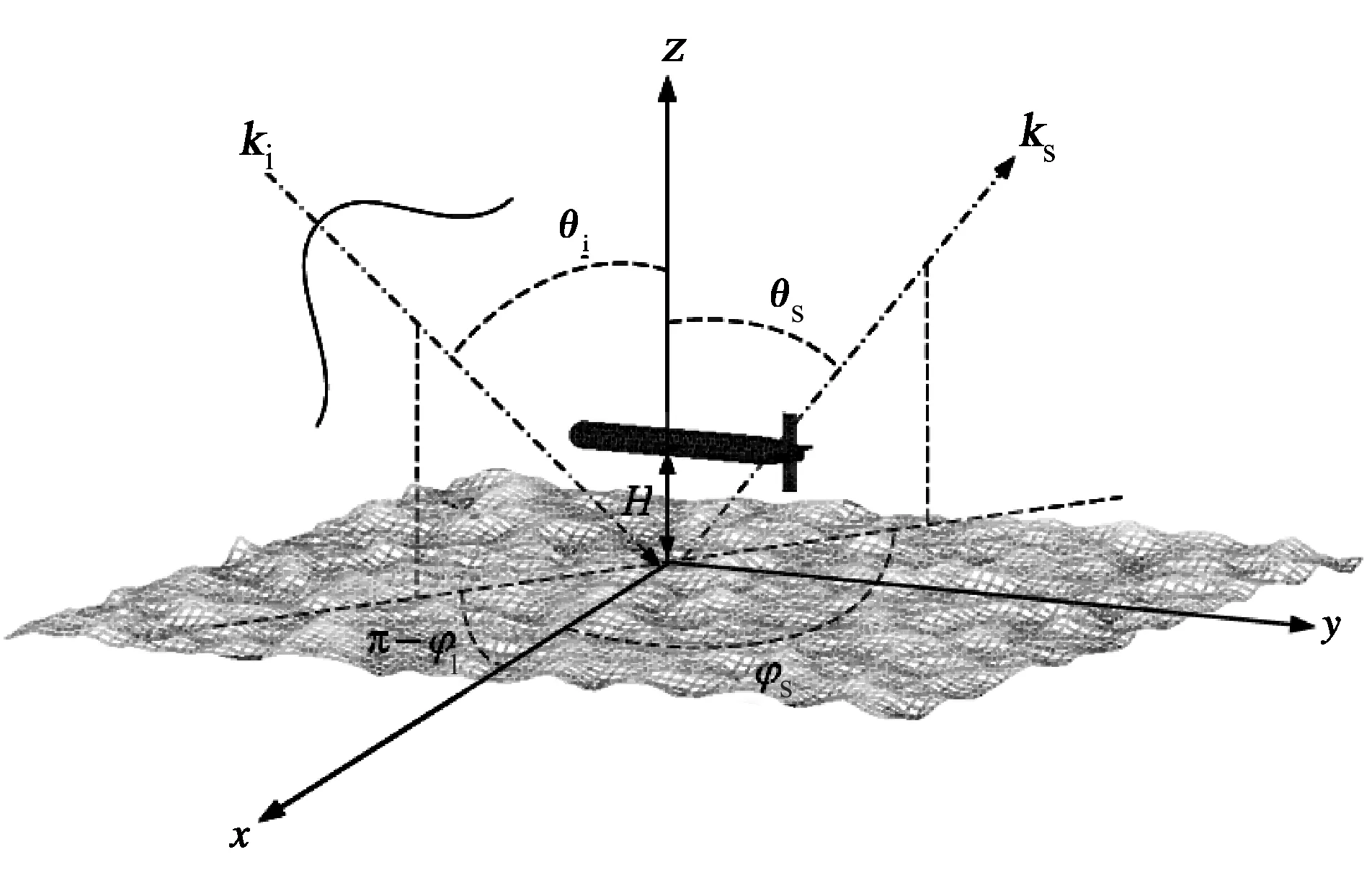
圖1 海面上導(dǎo)體目標(biāo)示意圖

當(dāng)粗糙面上沒(méi)有目標(biāo)時(shí)，滿足磁場(chǎng)邊界積分方程(MFIE)：

n′×Hs(r′)ds′

(1)

式中：Hinc(r)為入射磁場(chǎng)；n為粗糙面表面法向量；S指粗糙面表面；g(r，r′)=(r-r′)G(R)，

自由空間中的金屬目標(biāo)滿足電場(chǎng)邊界積分方程(EFIE)

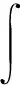
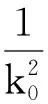
Hb(r′)))]g(r，r′)ds′

(2)

式中：Einc(r)為入射電場(chǎng)；nb為目標(biāo)表面法向量；Sb指目標(biāo)表面；k0為自由空間波常數(shù)； μ0為區(qū)域內(nèi)磁導(dǎo)率。

當(dāng)目標(biāo)與粗糙面同時(shí)存在時(shí)，必須考慮目標(biāo)與粗糙面的相互作用，由等效電流原理，粗糙面對(duì)目標(biāo)的散射貢獻(xiàn)為

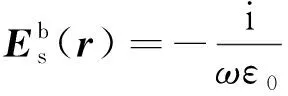
(3)

式中：Js(r)=n×Hs(r)，表示粗糙面表面電流；ε0為區(qū)域內(nèi)介電常數(shù)。

目標(biāo)對(duì)粗糙面的散射貢獻(xiàn)為

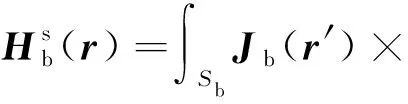
(4)

式中：Jb(r)=nb×Hb(r)，表示目標(biāo)表面電流。

結(jié)合式(1)和(2)，可以得到目標(biāo)與粗糙面的耦合積分方程組為

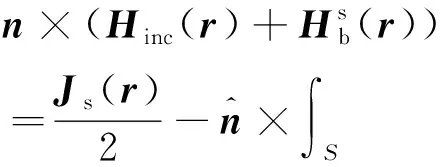
(5a)

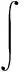
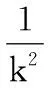
(5b)

1.2 E-PILE+SMFIA/CAG算法

將式(5)看成一個(gè)整體，直接運(yùn)用MoM可以得到如下線性方程組

ZI=V

(6)

式中：Z為總的阻抗矩陣，它既包括粗糙面的阻抗矩陣，又包括目標(biāo)的阻抗矩陣，以及目標(biāo)與粗糙面之間的相互作用阻抗矩陣，維數(shù)為2(N+M)×2(N+M)(N為粗糙面表面的未知量，M為目標(biāo)表面的未知量)；I為所求未知向量為

(7)

上標(biāo)T表示轉(zhuǎn)秩，Ir表示粗糙面的未知向量；V為激勵(lì)向量，包括目標(biāo)的激勵(lì)向量Vo和粗糙面的激勵(lì)向量Vr為

(8)

為了有效地求解線性方程組，將阻抗矩陣Z分成四塊

(9)

式中：Zo表示目標(biāo)自身的阻抗矩陣；Zr表示單層粗糙面自身的阻抗矩陣；Zo→r與Zr→o表示粗糙面與目標(biāo)相互作用的阻抗矩陣。對(duì)阻抗矩陣Z求逆可得

(10)

式中：

T=(Zo-Zr→o(Zr)-1Zo→r)-1

(11a)

U=-(Zo-Zr→o(Zr)-1Zo→r)-1Zr→o(Zr)-1

(11b)

Q=-(Zr)-1Zo→r(Zo-Zr→o(Zr)-1Zo→r)-1

(11c)

W= (Zr)-1+(Zr)-1Zo→r(Zo-Zr→o(Zr)-1Zo→r)-1×

Zr→o(Zr)-1

(11d)

所求未知向量I為

(12)

結(jié)合式(8)和式(9)，可以得到粗糙面未知向量

Io=(Zo-Zr→o(Zr)-1Zo→r)-1(Vo-Zr→o(Zr)-1Vr)

= (I-(Zo)-1Zr→o(Zr)-1Zo→r)-1(Zo)-1×

(Vo-Zr→o(Zr)-1Vr)

I為單位矩陣，定義特征矩陣為

Mc=(Zo)-1Zr→o(Zr)-1Zo→r

(13)

則由矩陣級(jí)數(shù)的求和理論，當(dāng)Mc為收斂矩陣時(shí)，有

(14)

數(shù)值計(jì)算中，矩陣的階數(shù)必須適當(dāng)?shù)慕財(cái)啵x截?cái)嚯A數(shù)為pPILE，結(jié)合式(12)和(14)可得

(15)

式中：

(16)

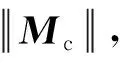
1.3 錐形入射波與散射系數(shù)

為避免人為截?cái)啻植诿嬉鸬倪吘壭?yīng)，采用錐形波入射[14]，限于篇幅，本文只考慮水平極化入射波情況，表達(dá)式為

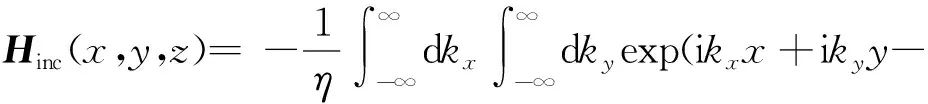
ikzz)·ETE(kx，ky)h(-kz)

(17)

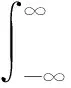
ikzz)·ETE(kx，ky)e(-kz)

(18)

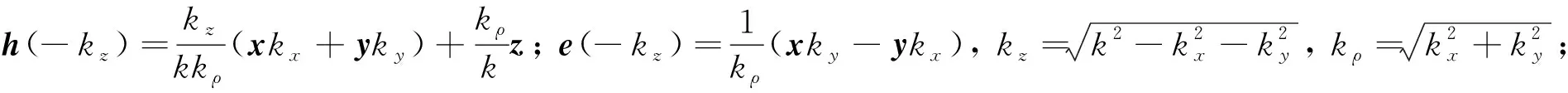
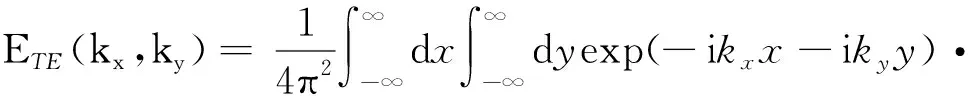
exp(i(kixx+kiyy)(1+w))exp(-t)

(19)

其中

t=tx+ty=(x2+y2)/g2

g參數(shù)控制錐形入射波的寬度。

定義雙站散射系數(shù)

(20)

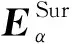
2.數(shù)值分析

2.1 算法的有效性與收斂性驗(yàn)證

采用具有PM海浪譜的隨機(jī)粗糙面模擬實(shí)際海洋面[16]。PM譜是以風(fēng)速為參量充分成長(zhǎng)狀態(tài)的海浪頻譜，是由觀測(cè)得到的純經(jīng)驗(yàn)譜，三維PM譜具有如下形式

(21)

定義迭代誤差

(22)

式中：Ztotal表示總的阻抗矩陣，它既包括粗糙面的阻抗矩陣，又包括目標(biāo)的阻抗矩陣；p表示階數(shù)。

以海洋粗糙面上方的金屬球體(見(jiàn)圖2)為例，驗(yàn)證算法的有效性。球體位于海面的正上方，球心距離海面高度為H，海面大小為L(zhǎng)x×Ly=10λ×10λ，風(fēng)速U19.5=5 m/s，此時(shí)海面方差h=0.133 4 m.入射波波長(zhǎng)取λ=1 m，入射角θi=30o，φi=0o，φv=0，錐形波參數(shù)g=Lx/3.海面剖分密度為每平方波長(zhǎng)上64個(gè)采樣點(diǎn)，產(chǎn)生6 400個(gè)采樣點(diǎn)，12 800個(gè)未知數(shù)，強(qiáng)作用距離rd=2.5λ.如無(wú)特殊說(shuō)明，文中所有結(jié)果均是對(duì)相同參數(shù)粗糙面實(shí)現(xiàn)10次取平均的結(jié)果。圖3所示為球體半徑取0.5λ，高度H=1.0λ，p取不同數(shù)值時(shí)實(shí)現(xiàn)一次的散射系數(shù)，同時(shí)給出了誤差大小，并與運(yùn)用傳統(tǒng)MoM得到的結(jié)果進(jìn)行了對(duì)比。由圖3可知，隨著p的增大，誤差迅速減小，當(dāng)p=2時(shí)兩種方法結(jié)果完全吻合。

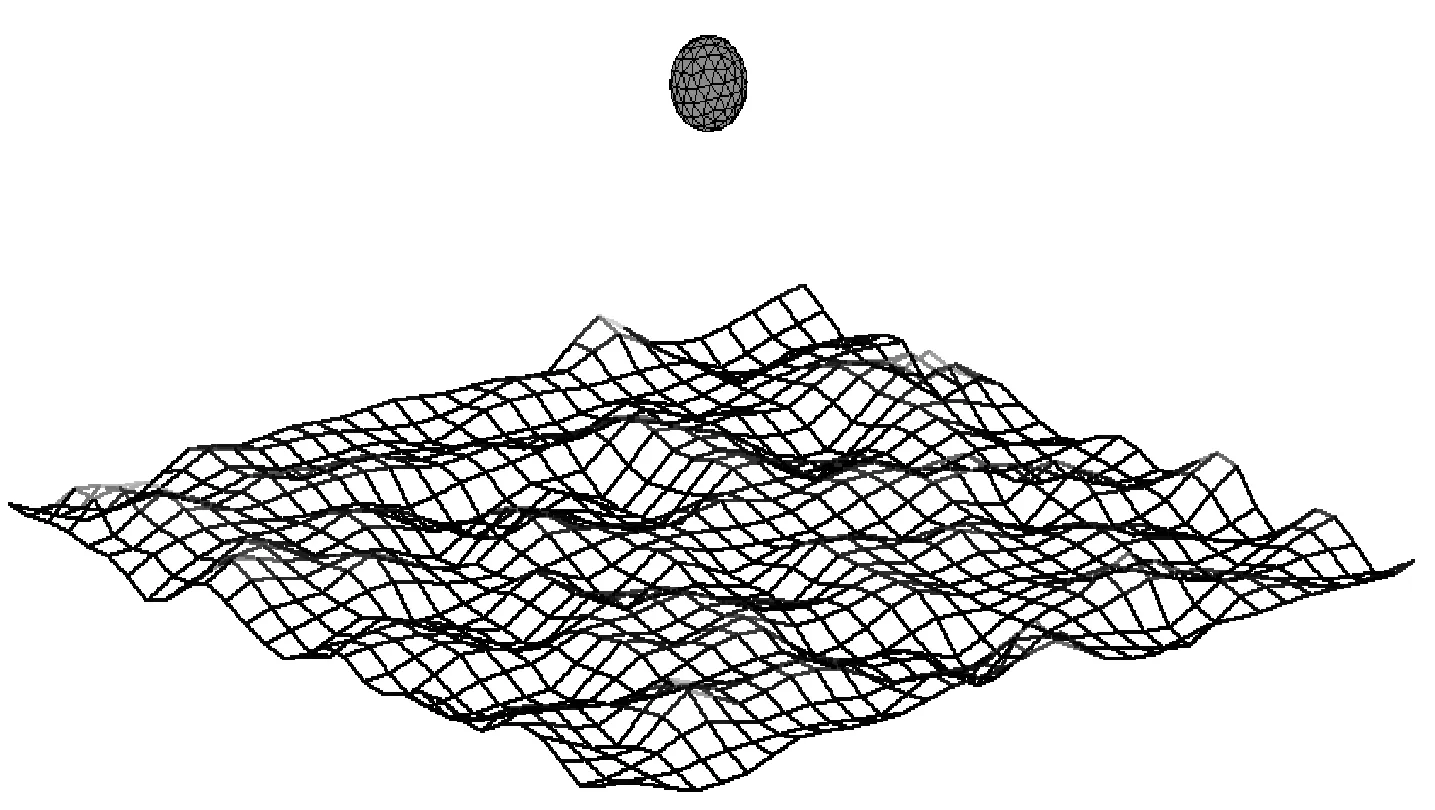
圖2 海面上方的金屬球體

驗(yàn)證算法的收斂性。其他參數(shù)不變，目標(biāo)分別取半徑為0.5λ的球體、圓柱(底面半徑為0.5λ，高為1λ)、邊長(zhǎng)為1λ的立方體，目標(biāo)表面剖分的三角面元個(gè)數(shù)分別為1 038、1 485和1 884，距離海面高度H=1.0λ，目標(biāo)尺寸相對(duì)于粗糙面的尺寸比較小(約為1： 100)，近似等效于目標(biāo)與無(wú)限大粗糙面之間的相互作用，此時(shí)，目標(biāo)可認(rèn)為是平面波入射。圖4所示為由式(22)計(jì)算相應(yīng)的迭代誤差隨階數(shù)p的變化結(jié)果，由圖可知，隨著階數(shù)p的增大，誤差成指數(shù)級(jí)衰減速度，且目標(biāo)為球體時(shí)收斂速度最快，目標(biāo)為立方體時(shí)收斂速度最慢，這是由于立方體目標(biāo)體積較大，與海面相互作用較強(qiáng)造成的，但所有結(jié)果均滿足計(jì)算精度要求，證明了本文算法對(duì)任意形狀目標(biāo)都具有良好的收斂性。計(jì)算所需時(shí)間見(jiàn)表1，可以發(fā)現(xiàn)，與MoM相比，E-PILE+SMFIA/CAG計(jì)算時(shí)間大大減少。

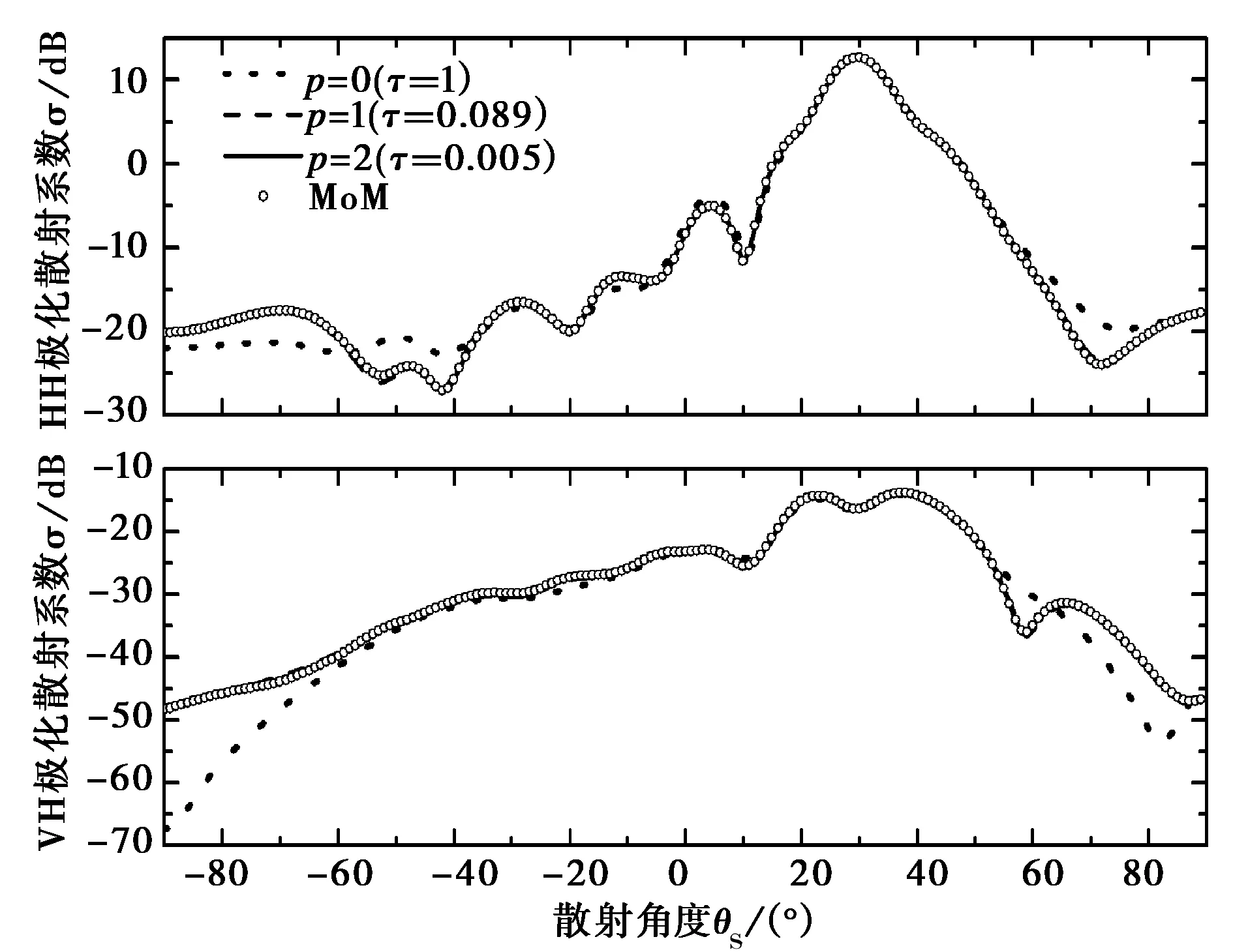
圖3 算法的驗(yàn)證

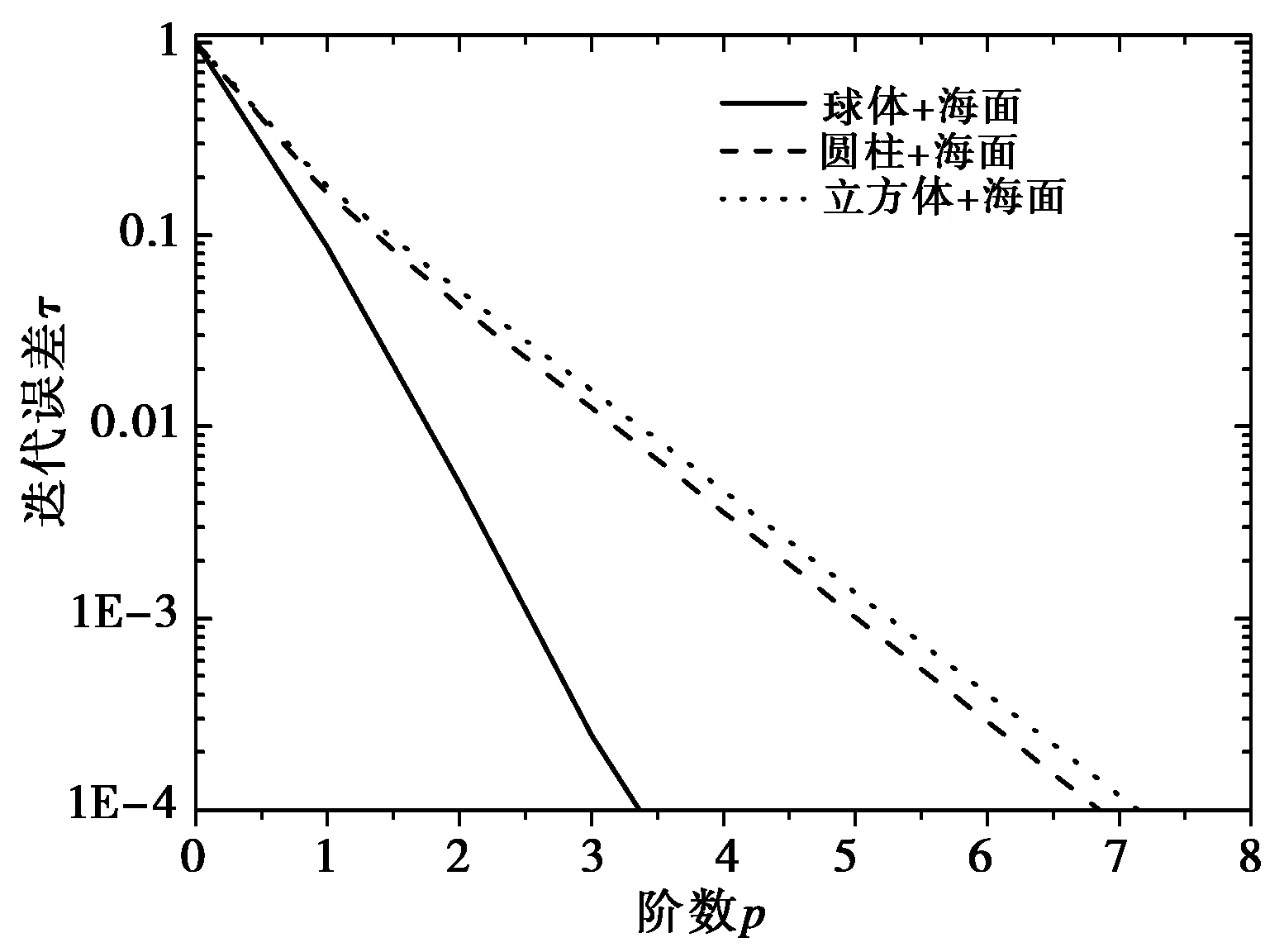
圖4 迭代誤差變化趨勢(shì)

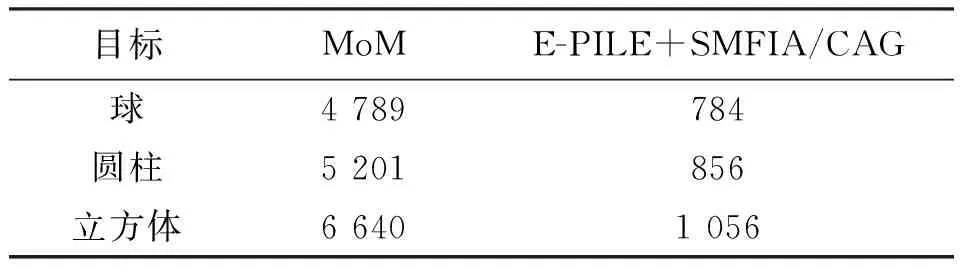
目標(biāo)MoME-PILE+SMFIA/CAG球4 789784圓柱5 201856立方體6 6401 056

2.2 結(jié)果分析與討論

計(jì)算海面上方金屬球體的雙站散射系數(shù)，球體半徑R=0.5λ，高度H=1.0λ，收斂精度取τ≤1%(對(duì)應(yīng)pPILE=2)。圖5(a)給出了HH和VH極化散射系數(shù)隨方位角θs變化情況，圖中還給出了只有海面時(shí)的散射系數(shù)，海面上方有無(wú)目標(biāo)時(shí)HH極化和VH極化散射系數(shù)在鏡面放射方向均有峰值，當(dāng)海面上方有目標(biāo)時(shí)，散射系數(shù)在除鏡面方向外的角度范圍內(nèi)明顯增大，尤其在后向散射方向更為明顯，同時(shí)由圖可知，VH極化散射系數(shù)要比HH極化散射系數(shù)小兩個(gè)數(shù)量級(jí)。HH和VH極化散射系數(shù)隨方位角φs的變化見(jiàn)圖5(b)(θs=θi=30°)，由圖可知，海面上有目標(biāo)時(shí)，HH極化散射系數(shù)在20°～160°范圍內(nèi)增大，在90°～150°范圍內(nèi)變化最為明顯，VH極化散射系數(shù)在所有角度都增大。

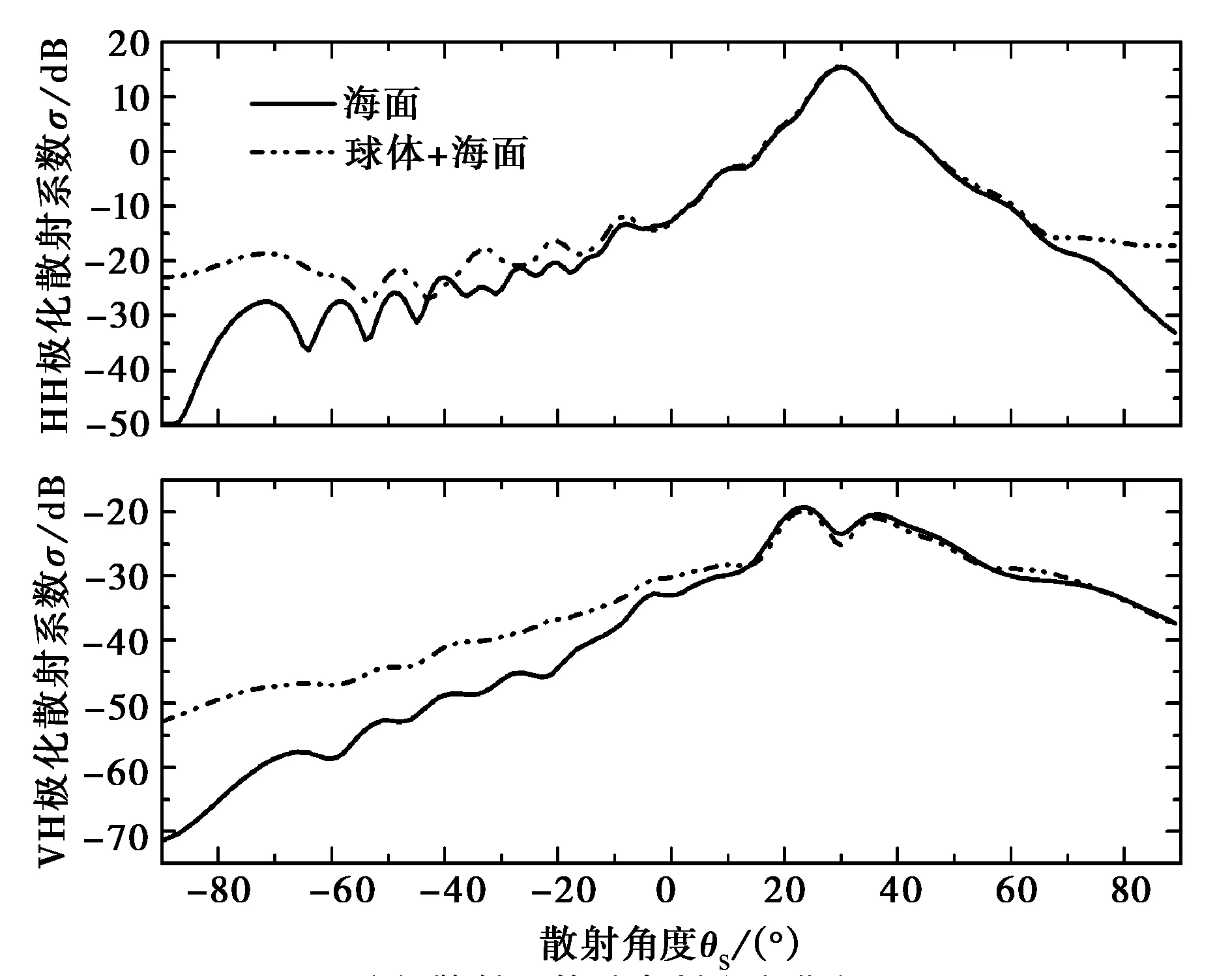
(a) 散射系數(shù)隨高低角變化(φs=0°)

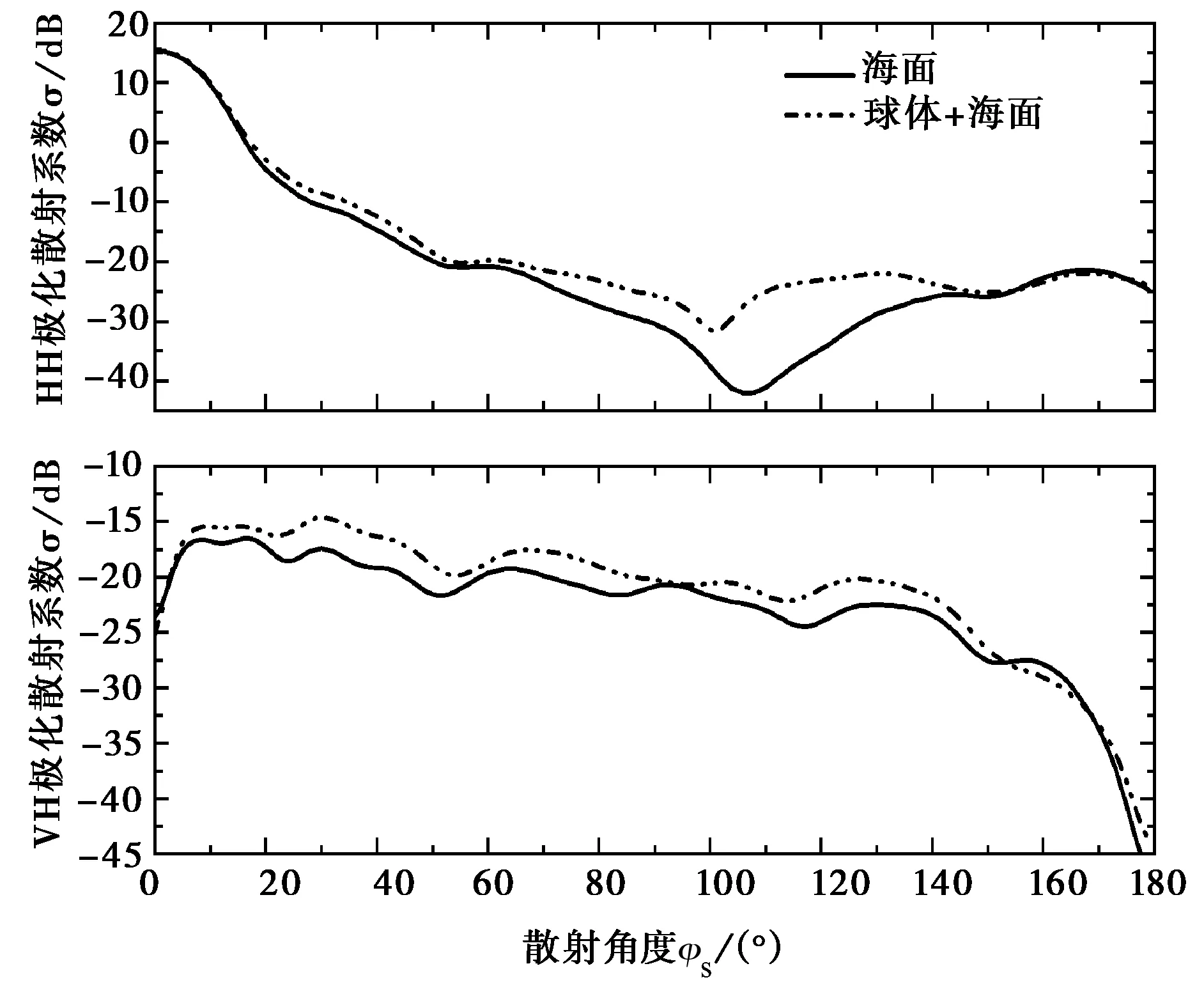
(b) 散射系數(shù)隨方位角變化(θs=30°)圖5 海面上球體散射系數(shù)

其他參數(shù)不變，令pPILE=4，圖6(a)和圖6(b)分別是海面上目標(biāo)為圓柱和立方體時(shí)的散射系數(shù)，其中圓柱參數(shù)：底面半徑為0.5λ，高為1λ，立方體邊長(zhǎng)為1λ.結(jié)合圖5(a)可知，當(dāng)目標(biāo)為立方體時(shí)散射系數(shù)最大，目標(biāo)為圓柱時(shí)次之，當(dāng)目標(biāo)為球時(shí)散射系數(shù)最小，但都明顯強(qiáng)于無(wú)目標(biāo)時(shí)海面的散射系數(shù)。這是由于立方體體積最大，與海面的相互作用較強(qiáng)。因此，當(dāng)海面上方目標(biāo)為立方體時(shí)散射系數(shù)變化最明顯，球體積最小，與海面的相互作用較小；當(dāng)目標(biāo)為球時(shí)散射系數(shù)變化最小。由此可知，海面上有目標(biāo)時(shí)的散射系數(shù)明顯大于無(wú)目標(biāo)時(shí)的散射系數(shù)，它們之間的差異正體現(xiàn)了目標(biāo)與粗糙面的相互作用，并且它們之間的相互作用隨目標(biāo)體積的增大而增強(qiáng)。同時(shí)由圖可知，當(dāng)海面上方有目標(biāo)時(shí)VH極化散射系數(shù)變化比HH極化散射系數(shù)變化明顯，這對(duì)地海面背景中目標(biāo)的探測(cè)與識(shí)別具有一定的理論指導(dǎo)意義。

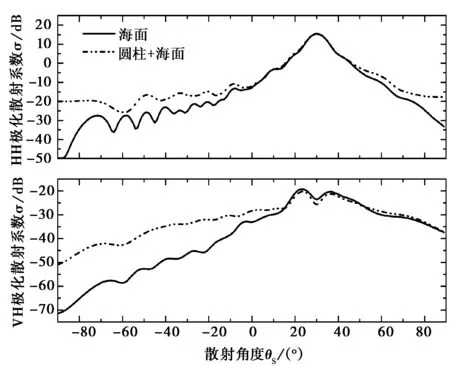
(a) 海面上方圓柱散射系數(shù)

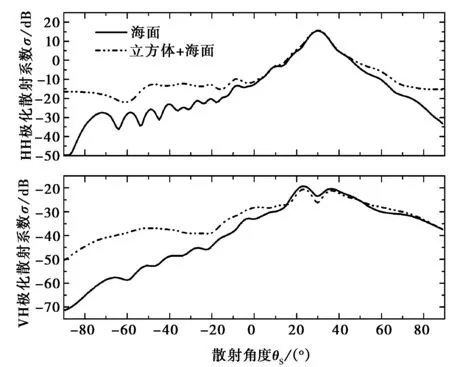
(b) 海面上方立方體散射系數(shù)圖6 海面上目標(biāo)散射系數(shù)

討論海面上方存在復(fù)雜目標(biāo)的情況。海面上方目標(biāo)為導(dǎo)彈模型(如圖1所示)，導(dǎo)彈模型見(jiàn)圖7，長(zhǎng)度為4.9 m，彈體半徑為0.25 m，翼展為2 m.海面大小取Lx×Ly=40λ×40λ，剖分密度為每平方波長(zhǎng)上64個(gè)采樣點(diǎn)，產(chǎn)生102 400個(gè)采樣點(diǎn)，204 800個(gè)未知數(shù)，為保證導(dǎo)彈與海面充分相互作用，取pPILE=5，其余參數(shù)不變。導(dǎo)彈距離海面高度分別取1λ、5λ和10λ，入射波從導(dǎo)彈頭部入射時(shí)散射系數(shù)如圖8(a)所示，此時(shí)入射角為φi=90°，入射波從導(dǎo)彈側(cè)面入射時(shí)(φi=0°)散射系數(shù)見(jiàn)圖8(b).由圖可知，隨著導(dǎo)彈距離海面高度增大，目標(biāo)與海面之間相互作用減小，除鏡面方向外，在其余角度散射系數(shù)均逐漸變小。

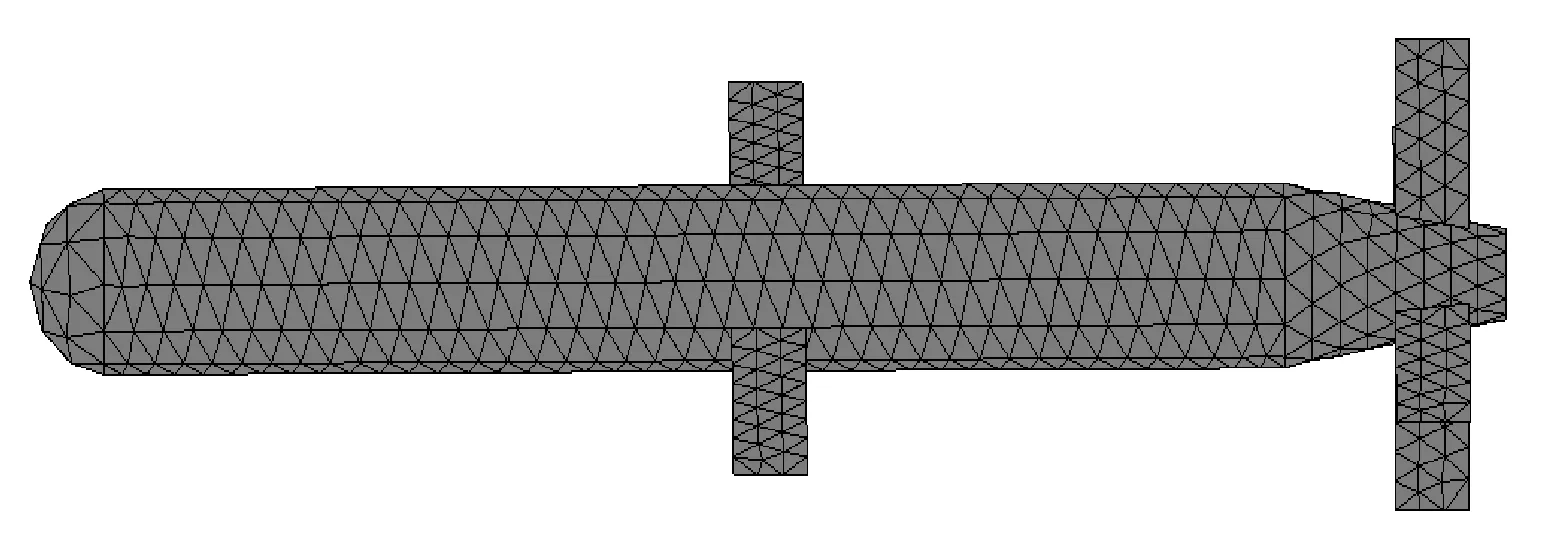
圖7 導(dǎo)彈模型示意圖

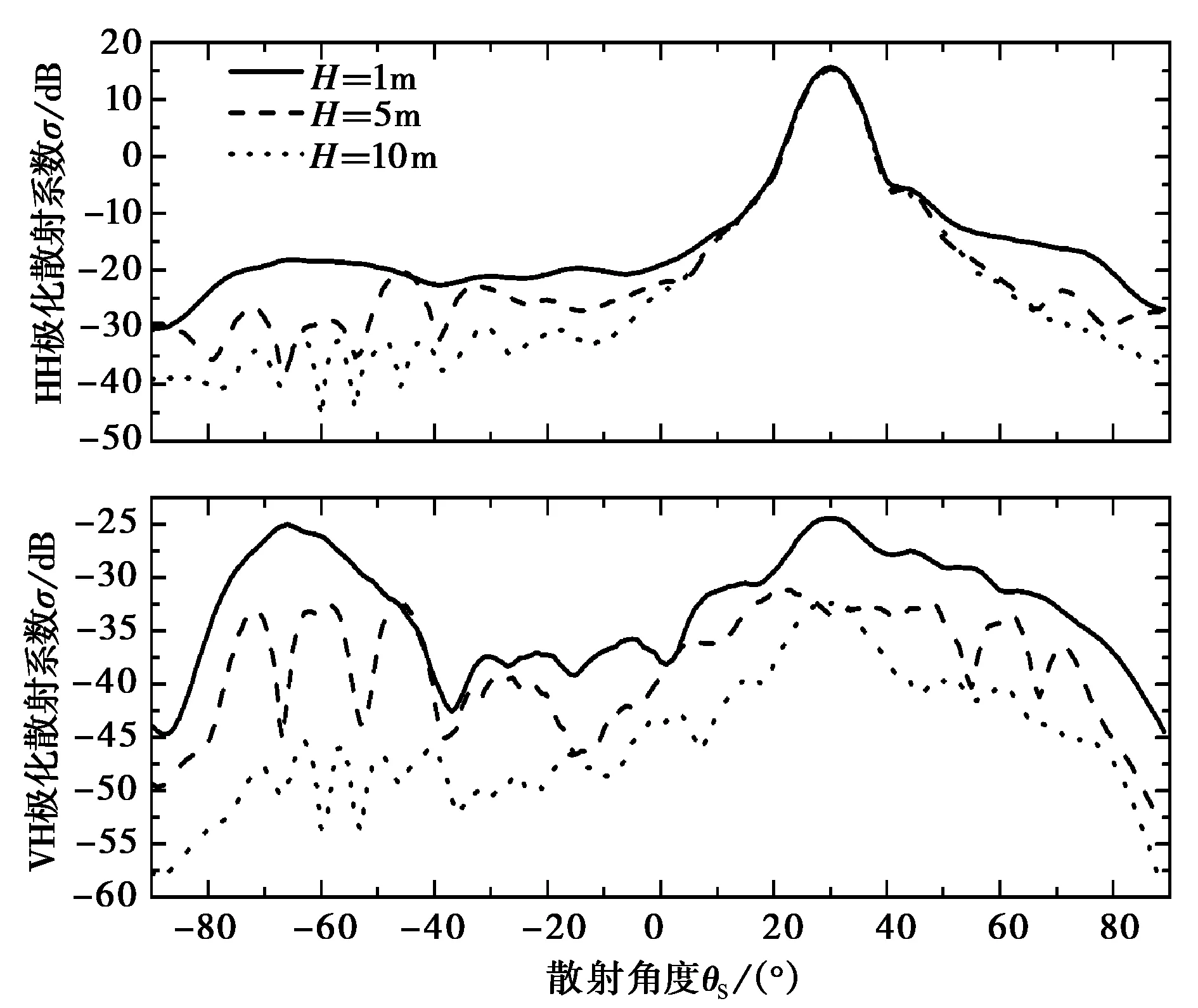
(a) 入射波頭部入射(φi=90°)

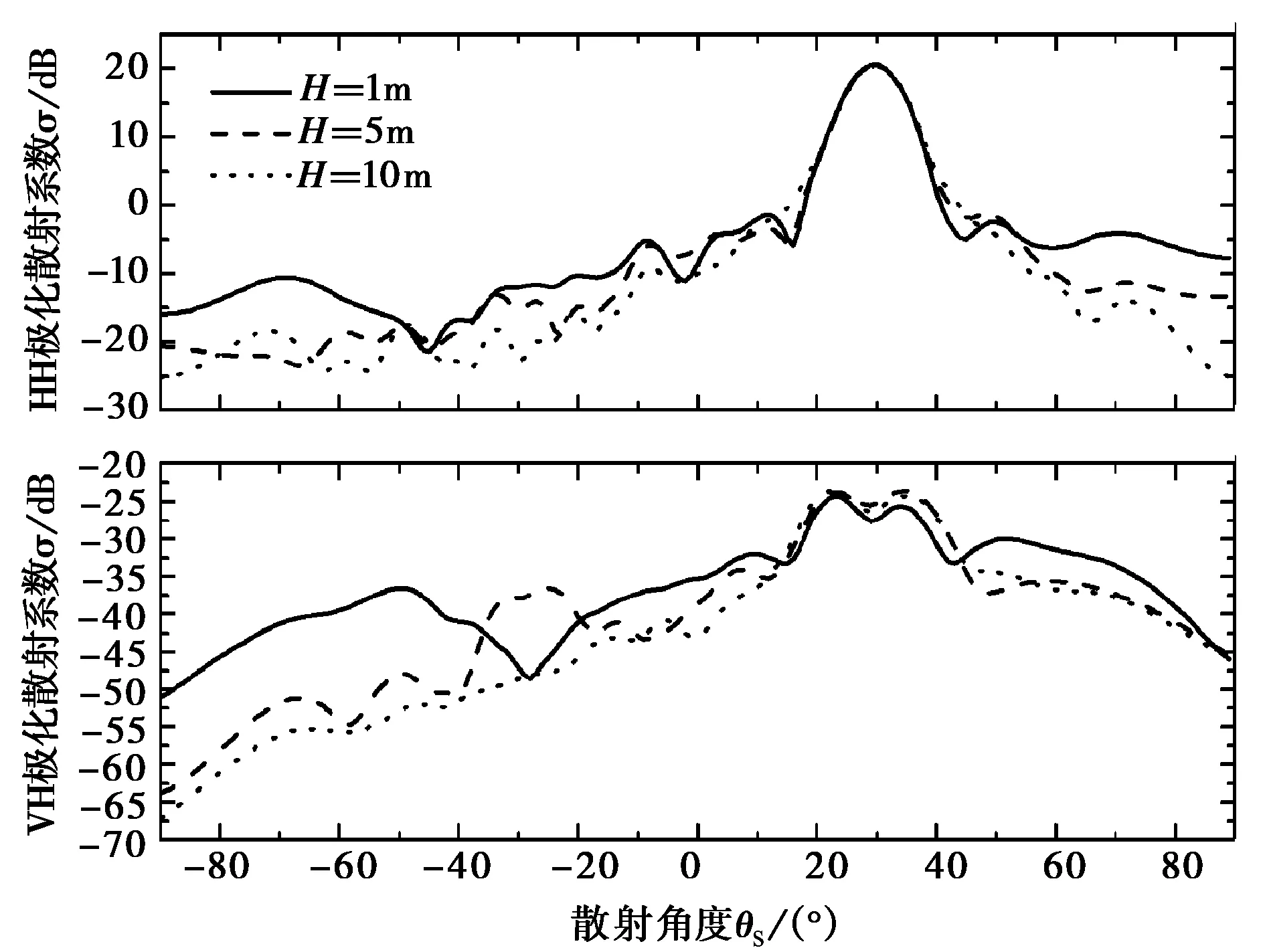
(b) 入射波頭部入射(φi=0°)圖8 不同目標(biāo)高度對(duì)應(yīng)的散射系數(shù)

研究海面上風(fēng)速對(duì)散射系數(shù)的影響。其他參數(shù)不變，導(dǎo)彈距離海面高度為5λ，海面上19.5 m處風(fēng)速分別取3 m/s、5 m/s和7 m/s，相應(yīng)的散射系數(shù)如圖9所示，其中圖9(a)是入射波從導(dǎo)彈頭部(φi=90°)入射的情況，圖9(b)是入射波從導(dǎo)彈側(cè)面(φi=0°)入射的情況。由圖可知，隨著海面上風(fēng)速增大，海面粗糙度增大，鏡面散射逐漸減弱而漫散射增強(qiáng)，因此，鏡面方向散射系數(shù)減小，而其余角度散射系數(shù)均有所增強(qiáng)，VH極化表現(xiàn)的更為明顯。同時(shí)由圖可知，同圖8結(jié)果相似，入射波從側(cè)面入射時(shí)的散射系數(shù)明顯大于入射波從頭部入射時(shí)的情況，這是由于入射波從導(dǎo)彈側(cè)面入射時(shí)的雷達(dá)照射面積遠(yuǎn)大于從頭部入射時(shí)的情況。

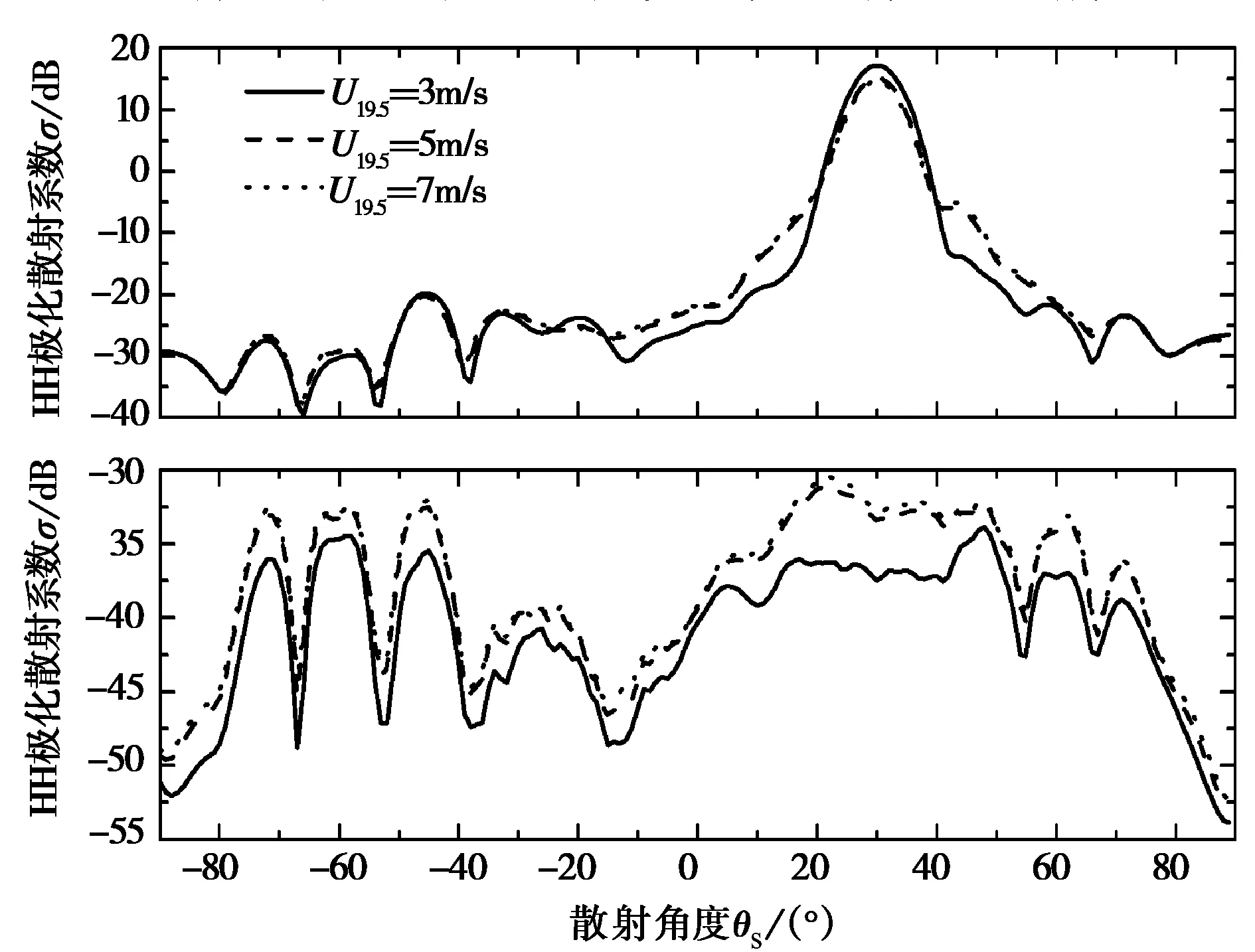
(a) 入射波頭部入射(φi=90°)

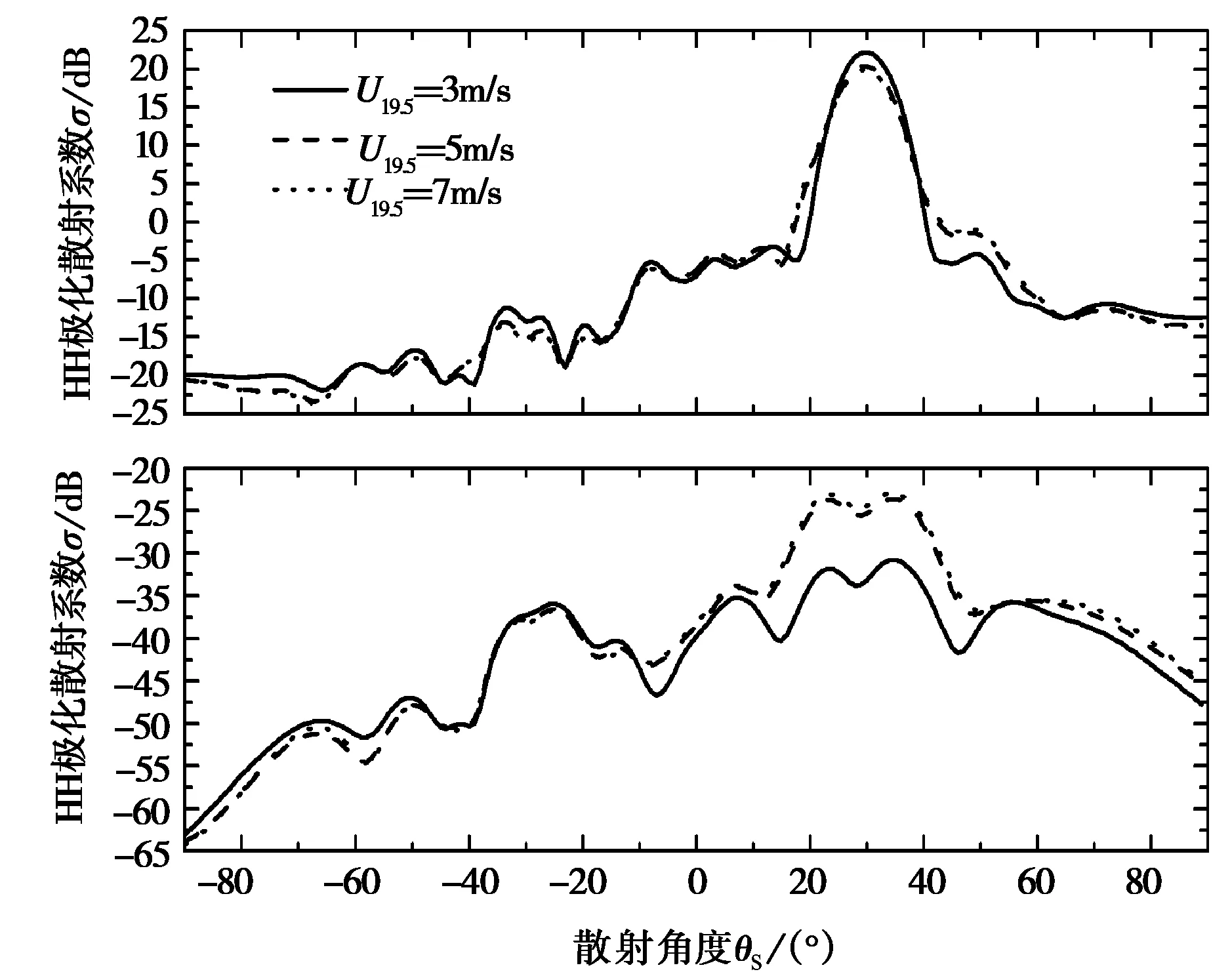
(b) 入射波側(cè)面入射(φi=0°)圖9 不同海面風(fēng)速對(duì)應(yīng)的散射系數(shù)

3. 結(jié) 論

結(jié)合SMFIA/CAG與基于RWG基函數(shù)的MoM，運(yùn)用迭代數(shù)值法快速計(jì)算了二維粗糙面上方三維金屬目標(biāo)的復(fù)合散射系數(shù)。該算法基于物理散射機(jī)理，理論簡(jiǎn)明，易于編程實(shí)現(xiàn)，并且不受粗糙面與目標(biāo)參數(shù)限制，可以計(jì)算復(fù)雜目標(biāo)與粗糙面的復(fù)合散射，是一種計(jì)算二維粗糙面上方目標(biāo)的復(fù)合電磁散射的快速有效算法。

結(jié)合PM譜的海洋粗糙面，應(yīng)用該算法計(jì)算了海面上方典型目標(biāo)的散射系數(shù)，驗(yàn)證了算法的有效性，討論了算法的收斂性。結(jié)果表明：當(dāng)海面上方有目標(biāo)時(shí)散射系數(shù)明顯大于沒(méi)有目標(biāo)時(shí)的情況。最后，運(yùn)用該算法計(jì)算了海面上導(dǎo)彈目標(biāo)的復(fù)合散射系數(shù)，并討論了目標(biāo)高度以及海面上風(fēng)速對(duì)散射系數(shù)的影響，結(jié)果表明：隨著目標(biāo)高度增加，散射系數(shù)逐漸減小，隨著海面上風(fēng)速增大，鏡面散射減小而漫反射增強(qiáng)。

[1] WANG X, WANG C F, GAN Y B, et al. Electromagnetic scattering from a circular target above or below rough surface[J]. PIER, 2003, 40: 208-226.

[2] 王 蕊, 郭立新, 王安琪. 不同土壤類型的粗糙地面與其下方埋藏目標(biāo)復(fù)合電磁散射研究[J]. 物理學(xué)報(bào), 2010, 59(5): 3179-3186.

WANG Rui, GUO Lixin, WANG Anqi. Investigation of electromagnetic scattering interaction between the buried target and the rough surface in different types of soil[J]. Acta Physica Sinica, 2010, 59(5): 3179-3186. (in Chinese)

[3] KUBICKE G, BOURLIER C, SAILLARD J. Scattering from canonical objects above a sea-like one-dimensional rough surface from a rigorous fast method[J]. Wave in Random and Complex Media, 2010, 20(1): 156-178.

[4] 姬偉杰, 童創(chuàng)明. 分層粗糙面下方介質(zhì)目標(biāo)散射的快速算法[J]. 電波科學(xué)學(xué)報(bào), 2010, 25(2): 336-342.

JI Weijie, TONG Chuangming. Fast calculation of EM scattering from layered rough surfaces with buried dielectric target[J]. Chinese Journal of Radio Science, 2010, 25(2): 336-342. (in Chinese)

[5] JOHNSON J T. A study of the four-path model for scattering from an object above a halfspace[J]. Microw Opt Technol Lett, 2001, 30(7): 130-134.

[6] 郭立新, 王運(yùn)華, 吳振森. 二維導(dǎo)體微粗糙面與其上方金屬平板的復(fù)合電磁散射研究[J]. 物理學(xué)報(bào), 2005, 54(11): 5130-5138.

GUO Lixin, WANG Yunhua, WU Zhensen. Electromagnetic scattering interaction between a conducting plate and a 2-D conducting slightly rough surface[J]. Acta Physica Sinica, 2005, 54 (11): 5130-5138. (in Chinese)

[7] 葉紅霞, 金亞秋. 三維隨機(jī)粗糙面上導(dǎo)體目標(biāo)散射的解析-數(shù)值混合算法[J]. 物理學(xué)報(bào), 2008, 57(2): 839-846.

YE Hongxia, JIN Yaqiu. A hybrid analytical-numerical algorithm for scattering from a 3-D target above a randomly rough surface[J]. Acta Physica Sinica, 2008, 57 (2): 839-846. (in Chinese)

[8] DENG Fangshun, HE Siyuan, CHEN Haitao, et al. Numerical simulation of vector wave scattering from the target and rough surface composite model with 3-D multilevel UV method[J]. IEEE Trans on Antennas Propag, 2010, 58(5): 1625-1634.

[9] KUANG Lei, JIN Yaqiu. Bistatic scattering from a three-dimensional object over a randomly rough surface using the FDTD algorithm[J]. IEEE Trans on Antennas Propag, 2007, 55(8): 1368-1376.

[10] EL-SHENAWEE M. The multiple interaction model for non-shallow scatterers buried beneath two dimen-sional random rough surfaces[J]. IEEE Trans on Geoscience and Remote Sensing, 2002, 40(4):982-987.

[11] CHEN Rushan, HU Yanqin, FAN Zhenghong, et al. An efficient surface integral equation solution to EM scattering by chiral objects above a lossy half space[J]. IEEE Trans on Antennas Propag, 2009, 57(11): 3586-3593.

[12] DECHAMPS N, DE BESUCOUDREY N, BOURLIER C, et al. Fast numerical method for electromagnetic scattering by rough layered interfaces: propagation-inside-layer-expansion method[J]. J Opti Soc Amer A, 2006, 23(2): 359-369.

[13] KUBICKE G, BOURLIER C, SAILLARD J. Scattering from canonical objects above a sea-like one-dimensional rough surface from a rigorous fast method[J]. Waves in Random and Complex Media, 2010, 20(1):156-178.

[14] TSANG L, KONG J A, DING K H. Scattering of Electromagnetic Waves: Numerical Simulations[M]. New York: John Wiley and Sons Inc, 2000: 278-285, 565-571.

[15] RAO S M, WLTON D R, GLISSON A W. Electromagnetic scattering by surfaces of arbitrary shape[J]. IEEE Trans on Antennas Propagat, 1982, 30(3): 409-418.

[16] TOPORKOV J V, BROWN G S. Numerieal simulations of scattering from time-varying, randomly rough surfaees[J]. IEEE Trans on Geosciences and Remote Sensing, 2000, 38(4): 1616-1625.